Adversarial Consistency and the Uniqueness of the Adversarial Bayes Classifier

Adversarial training is a common technique for learning robust classifiers. Prior work showed that convex surrogate losses are not statistically consistent in the adversarial context -- or in other words, a minimizing sequence of the adversarial surrogate risk will not necessarily minimize the adversarial classification error. We connect the consistency of adversarial surrogate losses to properties of minimizers to the adversarial classification risk, known as \emph{adversarial Bayes classifiers}. Specifically, under reasonable distributional assumptions, a convex loss is statistically consistent for adversarial learning iff the adversarial Bayes classifier satisfies a certain notion of uniqueness.

A Notion of Uniqueness for the Adversarial Bayes Classifier

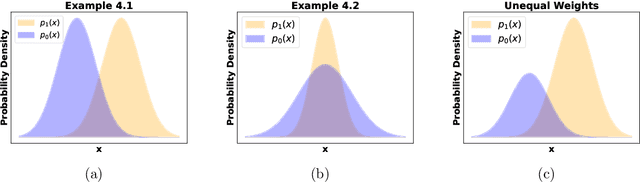
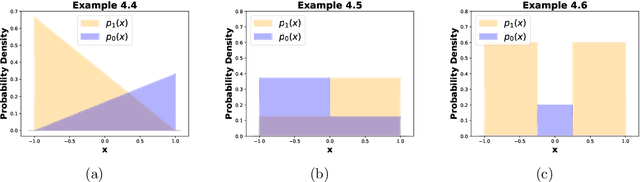
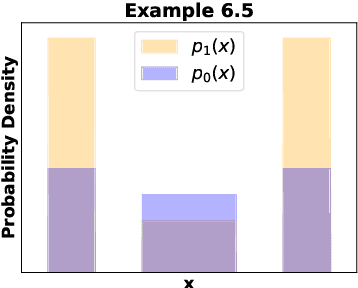
We propose a new notion of uniqueness for the adversarial Bayes classifier in the setting of binary classification. Analyzing this notion of uniqueness produces a simple procedure for computing all adversarial Bayes classifiers for a well-motivated family of one dimensional data distributions. This characterization is then leveraged to show that as the perturbation radius increases, certain notions of regularity improve for adversarial Bayes classifiers. We demonstrate with various examples that the boundary of the adversarial Bayes classifier frequently lies near the boundary of the Bayes classifier.

Robust Explanations for Deep Neural Networks via Pseudo Neural Tangent Kernel Surrogate Models

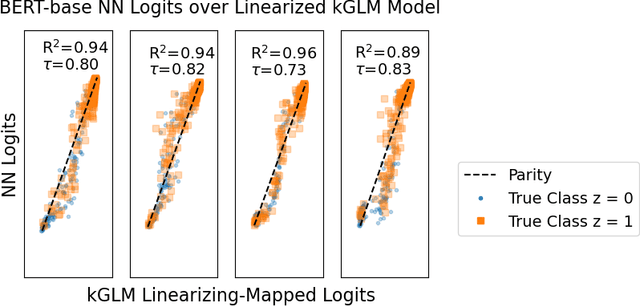
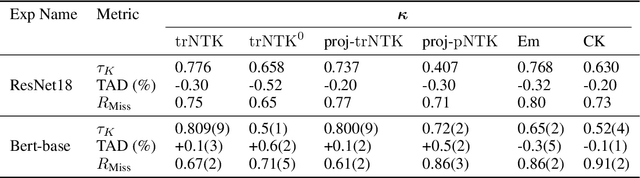
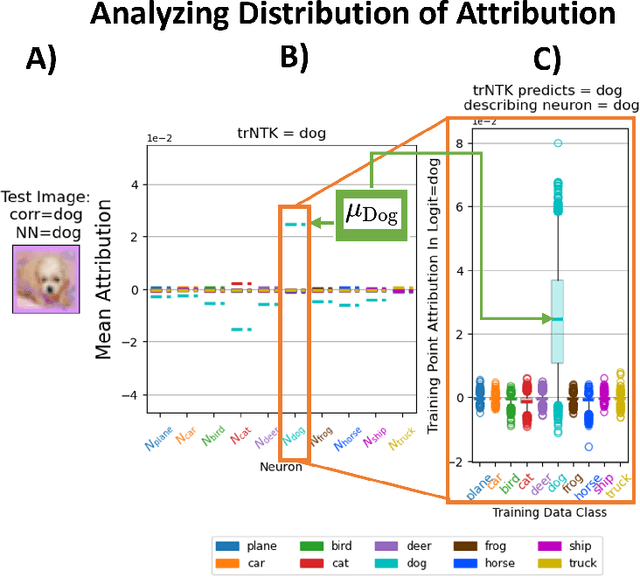
One of the ways recent progress has been made on explainable AI has been via explain-by-example strategies, specifically, through data attribution tasks. The feature spaces used to attribute decisions to training data, however, have not been compared against one another as to whether they form a truly representative surrogate model of the neural network (NN). Here, we demonstrate the efficacy of surrogate linear feature spaces to neural networks through two means: (1) we establish that a normalized psuedo neural tangent kernel (pNTK) is more correlated to the neural network decision functions than embedding based and influence based alternatives in both computer vision and large language model architectures; (2) we show that the attributions created from the normalized pNTK more accurately select perturbed training data in a data poisoning attribution task than these alternatives. Based on these observations, we conclude that kernel linear models are effective surrogate models across multiple classification architectures and that pNTK-based kernels are the most appropriate surrogate feature space of all kernels studied.

The Consistency of Adversarial Training for Binary Classification

Robustness to adversarial perturbations is of paramount concern in modern machine learning. One of the state-of-the-art methods for training robust classifiers is adversarial training, which involves minimizing a supremum-based surrogate risk. The statistical consistency of surrogate risks is well understood in the context of standard machine learning, but not in the adversarial setting. In this paper, we characterize which supremum-based surrogates are consistent for distributions absolutely continuous with respect to Lebesgue measure in binary classification. Furthermore, we obtain quantitative bounds relating adversarial surrogate risks to the adversarial classification risk. Lastly, we discuss implications for the $\cH$-consistency of adversarial training.

Existence and Minimax Theorems for Adversarial Surrogate Risks in Binary Classification

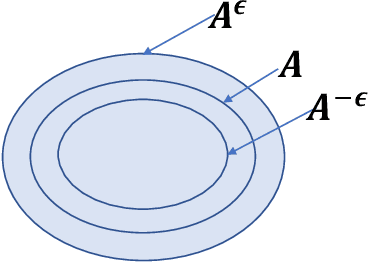
Adversarial training is one of the most popular methods for training methods robust to adversarial attacks, however, it is not well-understood from a theoretical perspective. We prove and existence, regularity, and minimax theorems for adversarial surrogate risks. Our results explain some empirical observations on adversarial robustness from prior work and suggest new directions in algorithm development. Furthermore, our results extend previously known existence and minimax theorems for the adversarial classification risk to surrogate risks.

On the Existence of the Adversarial Bayes Classifier

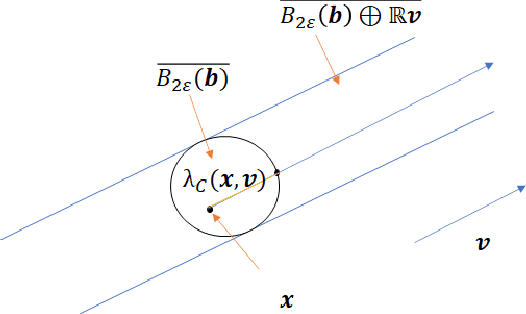
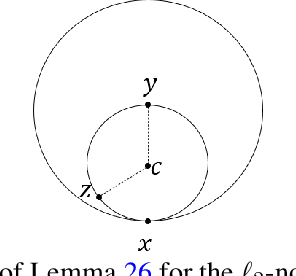
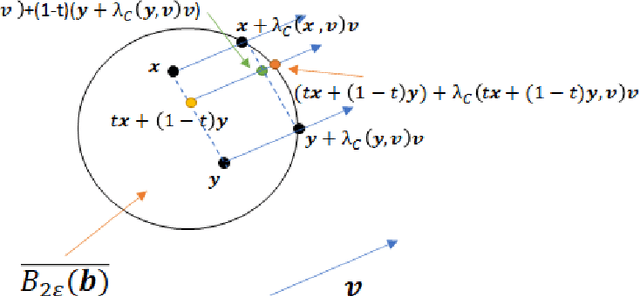
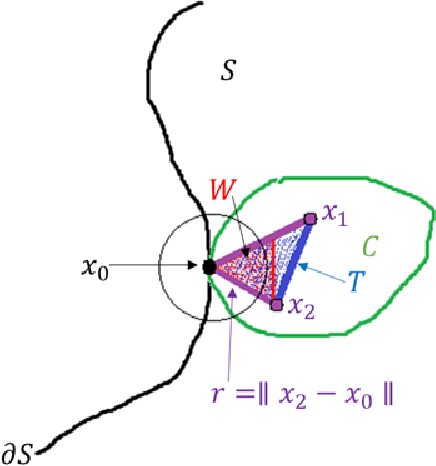
Adversarial robustness is a critical property in a variety of modern machine learning applications. While it has been the subject of several recent theoretical studies, many important questions related to adversarial robustness are still open. In this work, we study a fundamental question regarding Bayes optimality for adversarial robustness. We provide general sufficient conditions under which the existence of a Bayes optimal classifier can be guaranteed for adversarial robustness. Our results can provide a useful tool for a subsequent study of surrogate losses in adversarial robustness and their consistency properties. This manuscript is the extended version of the paper "On the Existence of the Adversarial Bayes Classifier" published in NeurIPS. The results of the original paper did not apply to some non-strictly convex norms. Here we extend our results to all possible norms.