Unraveling the Localized Latents: Learning Stratified Manifold Structures in LLM Embedding Space with Sparse Mixture-of-Experts

However, real-world data often exhibit complex local structures that can be challenging for single-model approaches with a smooth global manifold in the embedding space to unravel. In this work, we conjecture that in the latent space of these large language models, the embeddings live in a local manifold structure with different dimensions depending on the perplexities and domains of the input data, commonly referred to as a Stratified Manifold structure, which in combination form a structured space known as a Stratified Space. To investigate the validity of this structural claim, we propose an analysis framework based on a Mixture-of-Experts (MoE) model where each expert is implemented with a simple dictionary learning algorithm at varying sparsity levels. By incorporating an attention-based soft-gating network, we verify that our model learns specialized sub-manifolds for an ensemble of input data sources, reflecting the semantic stratification in LLM embedding space. We further analyze the intrinsic dimensions of these stratified sub-manifolds and present extensive statistics on expert assignments, gating entropy, and inter-expert distances. Our experimental results demonstrate that our method not only validates the claim of a stratified manifold structure in the LLM embedding space, but also provides interpretable clusters that align with the intrinsic semantic variations of the input data.

LSR-Adapt: Ultra-Efficient Parameter Tuning with Matrix Low Separation Rank Kernel Adaptation

Imposing an effective structural assumption on neural network weight matrices has been the major paradigm for designing Parameter-Efficient Fine-Tuning (PEFT) systems for adapting modern large pre-trained models to various downstream tasks. However, low rank based adaptation has become increasingly challenging due to the sheer scale of modern large language models. In this paper, we propose an effective kernelization to further reduce the number of parameters required for adaptation tasks. Specifically, from the classical idea in numerical analysis regarding matrix Low-Separation-Rank (LSR) representations, we develop a kernel using this representation for the low rank adapter matrices of the linear layers from large networks, named the Low Separation Rank Adaptation (LSR-Adapt) kernel. With the ultra-efficient kernel representation of the low rank adapter matrices, we manage to achieve state-of-the-art performance with even higher accuracy with almost half the number of parameters as compared to conventional low rank based methods. This structural assumption also opens the door to further GPU-side optimizations due to the highly parallelizable nature of Kronecker computations.

Learning To Help: Training Models to Assist Legacy Devices

Machine learning models implemented in hardware on physical devices may be deployed for a long time. The computational abilities of the device may be limited and become outdated with respect to newer improvements. Because of the size of ML models, offloading some computation (e.g. to an edge cloud) can help such legacy devices. We cast this problem in the framework of learning with abstention (LWA) in which the expert (edge) must be trained to assist the client (device). Prior work on LWA trains the client assuming the edge is either an oracle or a human expert. In this work, we formalize the reverse problem of training the expert for a fixed (legacy) client. As in LWA, the client uses a rejection rule to decide when to offload inference to the expert (at a cost). We find the Bayes-optimal rule, prove a generalization bound, and find a consistent surrogate loss function. Empirical results show that our framework outperforms confidence-based rejection rules.

LASERS: LAtent Space Encoding for Representations with Sparsity for Generative Modeling

Learning compact and meaningful latent space representations has been shown to be very useful in generative modeling tasks for visual data. One particular example is applying Vector Quantization (VQ) in variational autoencoders (VQ-VAEs, VQ-GANs, etc.), which has demonstrated state-of-the-art performance in many modern generative modeling applications. Quantizing the latent space has been justified by the assumption that the data themselves are inherently discrete in the latent space (like pixel values). In this paper, we propose an alternative representation of the latent space by relaxing the structural assumption than the VQ formulation. Specifically, we assume that the latent space can be approximated by a union of subspaces model corresponding to a dictionary-based representation under a sparsity constraint. The dictionary is learned/updated during the training process. We apply this approach to look at two models: Dictionary Learning Variational Autoencoders (DL-VAEs) and DL-VAEs with Generative Adversarial Networks (DL-GANs). We show empirically that our more latent space is more expressive and has leads to better representations than the VQ approach in terms of reconstruction quality at the expense of a small computational overhead for the latent space computation. Our results thus suggest that the true benefit of the VQ approach might not be from discretization of the latent space, but rather the lossy compression of the latent space. We confirm this hypothesis by showing that our sparse representations also address the codebook collapse issue as found common in VQ-family models.

Robust Explanations for Deep Neural Networks via Pseudo Neural Tangent Kernel Surrogate Models

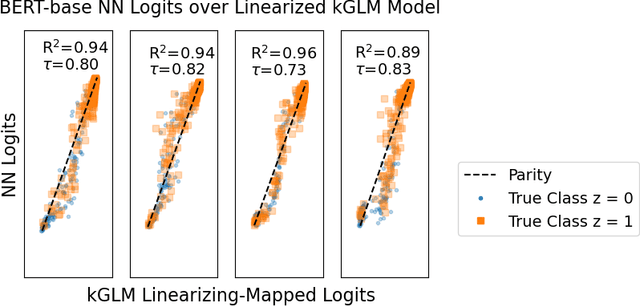
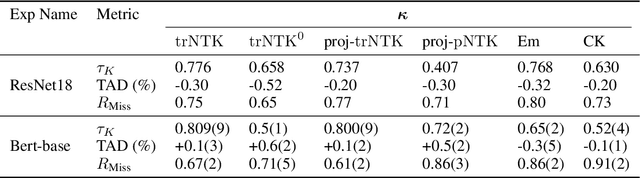
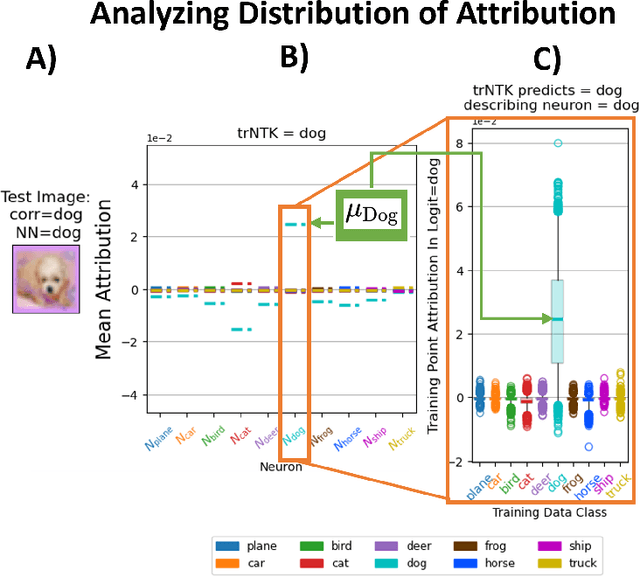
One of the ways recent progress has been made on explainable AI has been via explain-by-example strategies, specifically, through data attribution tasks. The feature spaces used to attribute decisions to training data, however, have not been compared against one another as to whether they form a truly representative surrogate model of the neural network (NN). Here, we demonstrate the efficacy of surrogate linear feature spaces to neural networks through two means: (1) we establish that a normalized psuedo neural tangent kernel (pNTK) is more correlated to the neural network decision functions than embedding based and influence based alternatives in both computer vision and large language model architectures; (2) we show that the attributions created from the normalized pNTK more accurately select perturbed training data in a data poisoning attribution task than these alternatives. Based on these observations, we conclude that kernel linear models are effective surrogate models across multiple classification architectures and that pNTK-based kernels are the most appropriate surrogate feature space of all kernels studied.

Spectral evolution and invariance in linear-width neural networks

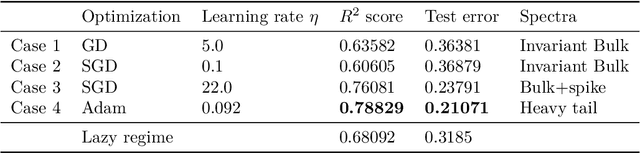
We investigate the spectral properties of linear-width feed-forward neural networks, where the sample size is asymptotically proportional to network width. Empirically, we show that the weight spectra in this high dimensional regime are invariant when trained by gradient descent for small constant learning rates and the changes in both operator and Frobenius norm are $\Theta(1)$ in the limit. This implies the bulk spectra for both the conjugate and neural tangent kernels are also invariant. We demonstrate similar characteristics for models trained with mini-batch (stochastic) gradient descent with small learning rates and provide a theoretical justification for this special scenario. When the learning rate is large, we show empirically that an outlier emerges with its corresponding eigenvector aligned to the training data structure. We also show that after adaptive gradient training, where we have a lower test error and feature learning emerges, both the weight and kernel matrices exhibit heavy tail behavior. Different spectral properties such as invariant bulk, spike, and heavy-tailed distribution correlate to how far the kernels deviate from initialization. To understand this phenomenon better, we focus on a toy model, a two-layer network on synthetic data, which exhibits different spectral properties for different training strategies. Analogous phenomena also appear when we train conventional neural networks with real-world data. Our results show that monitoring the evolution of the spectra during training is an important step toward understanding the training dynamics and feature learning.