Spectral evolution and invariance in linear-width neural networks
Paper and Code
Nov 11, 2022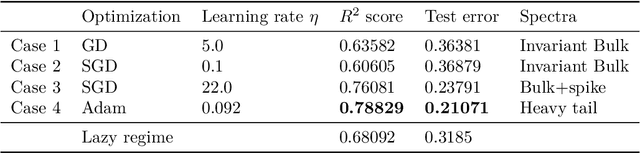



We investigate the spectral properties of linear-width feed-forward neural networks, where the sample size is asymptotically proportional to network width. Empirically, we show that the weight spectra in this high dimensional regime are invariant when trained by gradient descent for small constant learning rates and the changes in both operator and Frobenius norm are $\Theta(1)$ in the limit. This implies the bulk spectra for both the conjugate and neural tangent kernels are also invariant. We demonstrate similar characteristics for models trained with mini-batch (stochastic) gradient descent with small learning rates and provide a theoretical justification for this special scenario. When the learning rate is large, we show empirically that an outlier emerges with its corresponding eigenvector aligned to the training data structure. We also show that after adaptive gradient training, where we have a lower test error and feature learning emerges, both the weight and kernel matrices exhibit heavy tail behavior. Different spectral properties such as invariant bulk, spike, and heavy-tailed distribution correlate to how far the kernels deviate from initialization. To understand this phenomenon better, we focus on a toy model, a two-layer network on synthetic data, which exhibits different spectral properties for different training strategies. Analogous phenomena also appear when we train conventional neural networks with real-world data. Our results show that monitoring the evolution of the spectra during training is an important step toward understanding the training dynamics and feature learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge