A Notion of Uniqueness for the Adversarial Bayes Classifier
Paper and Code
Apr 25, 2024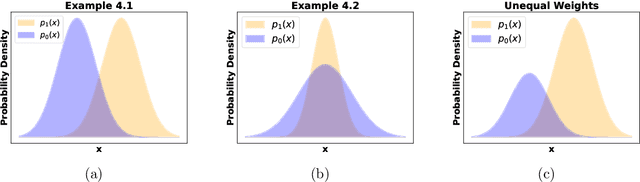
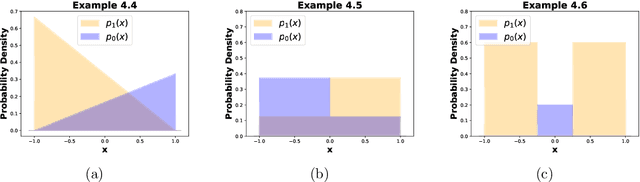
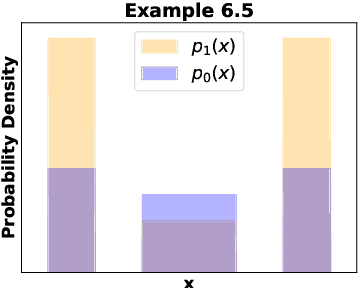
We propose a new notion of uniqueness for the adversarial Bayes classifier in the setting of binary classification. Analyzing this notion of uniqueness produces a simple procedure for computing all adversarial Bayes classifiers for a well-motivated family of one dimensional data distributions. This characterization is then leveraged to show that as the perturbation radius increases, certain notions of regularity improve for adversarial Bayes classifiers. We demonstrate with various examples that the boundary of the adversarial Bayes classifier frequently lies near the boundary of the Bayes classifier.
* 46 pages, 7 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge