Graph-Based Learning of Spectro-Topographical EEG Representations with Gradient Alignment for Brain-Computer Interfaces

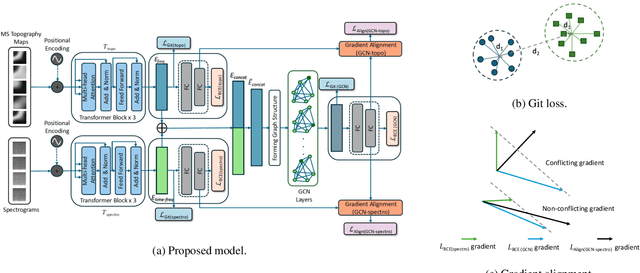
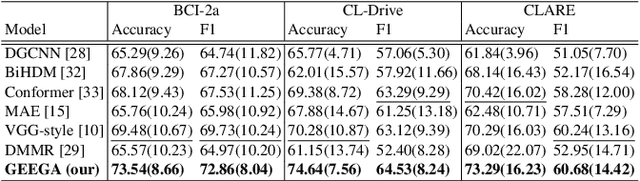
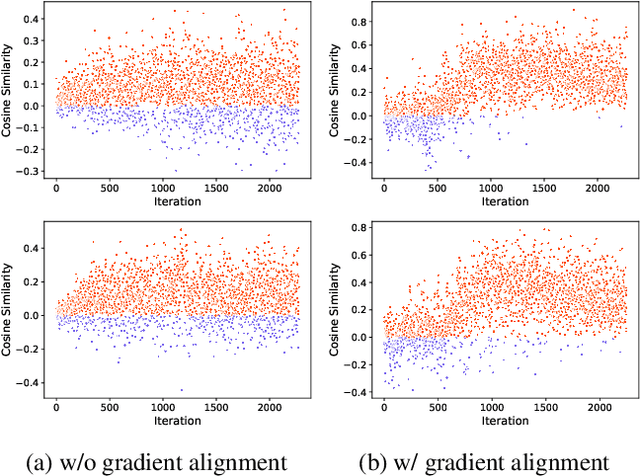
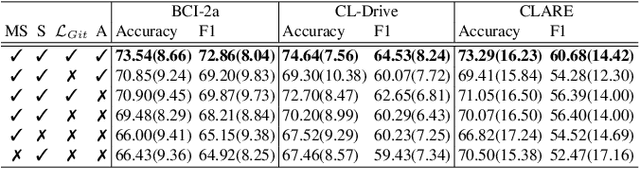
We present a novel graph-based learning of EEG representations with gradient alignment (GEEGA) that leverages multi-domain information to learn EEG representations for brain-computer interfaces. Our model leverages graph convolutional networks to fuse embeddings from frequency-based topographical maps and time-frequency spectrograms, capturing inter-domain relationships. GEEGA addresses the challenge of achieving high inter-class separability, which arises from the temporally dynamic and subject-sensitive nature of EEG signals by incorporating the center loss and pairwise difference loss. Additionally, GEEGA incorporates a gradient alignment strategy to resolve conflicts between gradients from different domains and the fused embeddings, ensuring that discrepancies, where gradients point in conflicting directions, are aligned toward a unified optimization direction. We validate the efficacy of our method through extensive experiments on three publicly available EEG datasets: BCI-2a, CL-Drive and CLARE. Comprehensive ablation studies further highlight the impact of various components of our model.

Multi-Domain EEG Representation Learning with Orthogonal Mapping and Attention-based Fusion for Cognitive Load Classification

We propose a new representation learning solution for the classification of cognitive load based on Electroencephalogram (EEG). Our method integrates both time and frequency domains by first passing the raw EEG signals through the convolutional encoder to obtain the time domain representations. Next, we measure the Power Spectral Density (PSD) for all five EEG frequency bands and generate the channel power values as 2D images referred to as multi-spectral topography maps. These multi-spectral topography maps are then fed to a separate encoder to obtain the representations in frequency domain. Our solution employs a multi-domain attention module that maps these domain-specific embeddings onto a shared embedding space to emphasize more on important inter-domain relationships to enhance the representations for cognitive load classification. Additionally, we incorporate an orthogonal projection constraint during the training of our method to effectively increase the inter-class distances while improving intra-class clustering. This enhancement allows efficient discrimination between different cognitive states and aids in better grouping of similar states within the feature space. We validate the effectiveness of our model through extensive experiments on two public EEG datasets, CL-Drive and CLARE for cognitive load classification. Our results demonstrate the superiority of our multi-domain approach over the traditional single-domain techniques. Moreover, we conduct ablation and sensitivity analyses to assess the impact of various components of our method. Finally, robustness experiments on different amounts of added noise demonstrate the stability of our method compared to other state-of-the-art solutions.

Learning Time-Series Representations by Hierarchical Uniformity-Tolerance Latent Balancing

We propose TimeHUT, a novel method for learning time-series representations by hierarchical uniformity-tolerance balancing of contrastive representations. Our method uses two distinct losses to learn strong representations with the aim of striking an effective balance between uniformity and tolerance in the embedding space. First, TimeHUT uses a hierarchical setup to learn both instance-wise and temporal information from input time-series. Next, we integrate a temperature scheduler within the vanilla contrastive loss to balance the uniformity and tolerance characteristics of the embeddings. Additionally, a hierarchical angular margin loss enforces instance-wise and temporal contrast losses, creating geometric margins between positive and negative pairs of temporal sequences. This approach improves the coherence of positive pairs and their separation from the negatives, enhancing the capture of temporal dependencies within a time-series sample. We evaluate our approach on a wide range of tasks, namely 128 UCR and 30 UAE datasets for univariate and multivariate classification, as well as Yahoo and KPI datasets for anomaly detection. The results demonstrate that TimeHUT outperforms prior methods by considerable margins on classification, while obtaining competitive results for anomaly detection. Finally, detailed sensitivity and ablation studies are performed to evaluate different components and hyperparameters of our method.

DMN-Guided Prompting: A Low-Code Framework for Controlling LLM Behavior

Large Language Models (LLMs) have shown considerable potential in automating decision logic within knowledge-intensive processes. However, their effectiveness largely depends on the strategy and quality of prompting. Since decision logic is typically embedded in prompts, it becomes challenging for end users to modify or refine it. Decision Model and Notation (DMN) offers a standardized graphical approach for defining decision logic in a structured, user-friendly manner. This paper introduces a DMN-guided prompting framework that breaks down complex decision logic into smaller, manageable components, guiding LLMs through structured decision pathways. We implemented the framework in a graduate-level course where students submitted assignments. The assignments and DMN models representing feedback instructions served as inputs to our framework. The instructor evaluated the generated feedback and labeled it for performance assessment. Our approach demonstrated promising results, outperforming chain-of-thought (CoT) prompting. Students also responded positively to the generated feedback, reporting high levels of perceived usefulness in a survey based on the Technology Acceptance Model.

AI-Enhanced Business Process Automation: A Case Study in the Insurance Domain Using Object-Centric Process Mining

Recent advancements in Artificial Intelligence (AI), particularly Large Language Models (LLMs), have enhanced organizations' ability to reengineer business processes by automating knowledge-intensive tasks. This automation drives digital transformation, often through gradual transitions that improve process efficiency and effectiveness. To fully assess the impact of such automation, a data-driven analysis approach is needed - one that examines how traditional and AI-enhanced process variants coexist during this transition. Object-Centric Process Mining (OCPM) has emerged as a valuable method that enables such analysis, yet real-world case studies are still needed to demonstrate its applicability. This paper presents a case study from the insurance sector, where an LLM was deployed in production to automate the identification of claim parts, a task previously performed manually and identified as a bottleneck for scalability. To evaluate this transformation, we apply OCPM to assess the impact of AI-driven automation on process scalability. Our findings indicate that while LLMs significantly enhance operational capacity, they also introduce new process dynamics that require further refinement. This study also demonstrates the practical application of OCPM in a real-world setting, highlighting its advantages and limitations.

OCPM$^2$: Extending the Process Mining Methodology for Object-Centric Event Data Extraction

Object-Centric Process Mining (OCPM) enables business process analysis from multiple perspectives. For example, an educational path can be examined from the viewpoints of students, teachers, and groups. This analysis depends on Object-Centric Event Data (OCED), which captures relationships between events and object types, representing different perspectives. Unlike traditional process mining techniques, extracting OCED minimizes the need for repeated log extractions when shifting the analytical focus. However, recording these complex relationships increases the complexity of the log extraction process. To address this challenge, this paper proposes a method for extracting OCED based on PM\inst{2}, a well-established process mining framework. Our approach introduces a structured framework that guides data analysts and engineers in extracting OCED for process analysis. We validate this framework by applying it in a real-world educational setting, demonstrating its effectiveness in extracting an Object-Centric Event Log (OCEL), which serves as the standard format for recording OCED, from a learning management system and an administrative grading system.

Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations

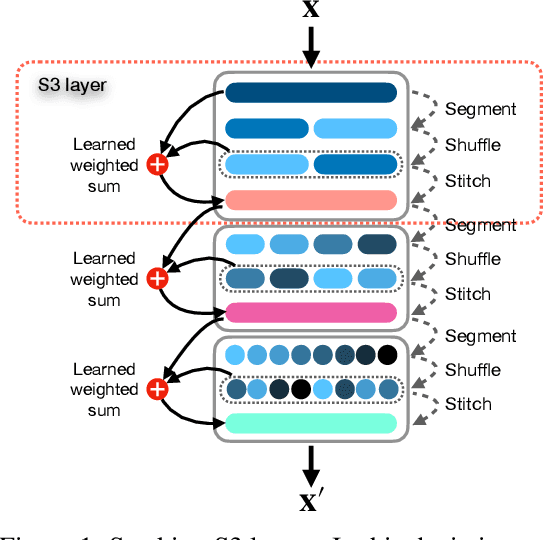
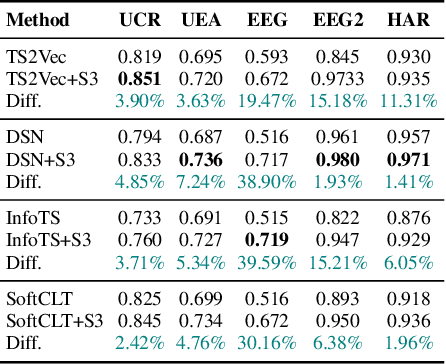
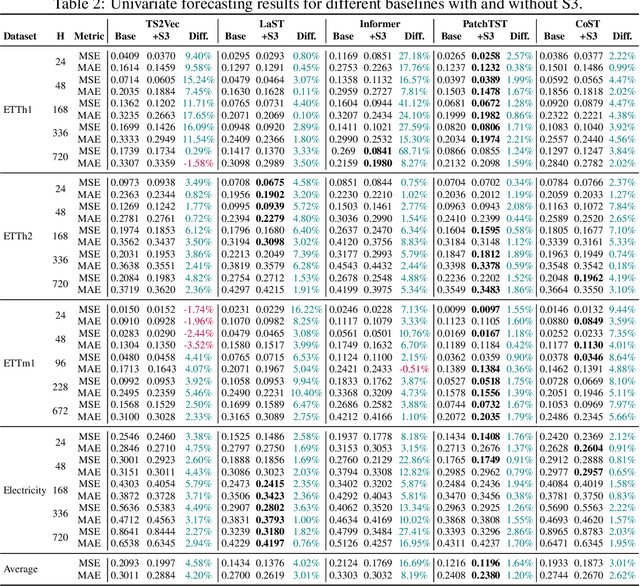
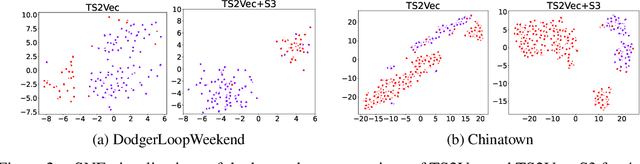
Existing approaches for learning representations of time-series keep the temporal arrangement of the time-steps intact with the presumption that the original order is the most optimal for learning. However, non-adjacent sections of real-world time-series may have strong dependencies. Accordingly we raise the question: Is there an alternative arrangement for time-series which could enable more effective representation learning? To address this, we propose a simple plug-and-play mechanism called Segment, Shuffle, and Stitch (S3) designed to improve time-series representation learning of existing models. S3 works by creating non-overlapping segments from the original sequence and shuffling them in a learned manner that is the most optimal for the task at hand. It then re-attaches the shuffled segments back together and performs a learned weighted sum with the original input to capture both the newly shuffled sequence along with the original sequence. S3 is modular and can be stacked to create various degrees of granularity, and can be added to many forms of neural architectures including CNNs or Transformers with negligible computation overhead. Through extensive experiments on several datasets and state-of-the-art baselines, we show that incorporating S3 results in significant improvements for the tasks of time-series classification and forecasting, improving performance on certain datasets by up to 68\%. We also show that S3 makes the learning more stable with a smoother training loss curve and loss landscape compared to the original baseline. The code is available at https://github.com/shivam-grover/S3-TimeSeries .

Adversarial Lagrangian Integrated Contrastive Embedding for Limited Size Datasets

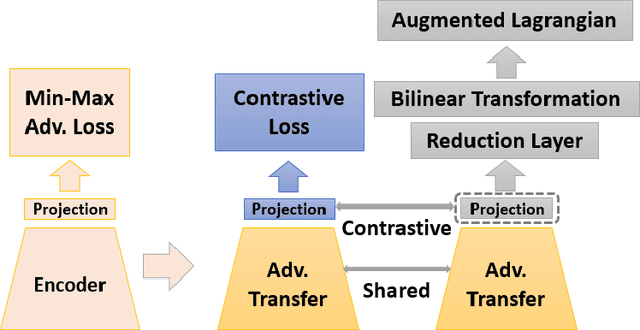
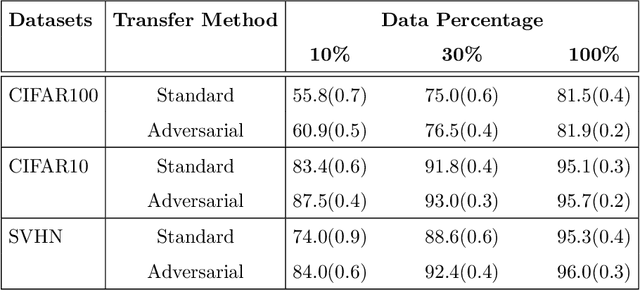
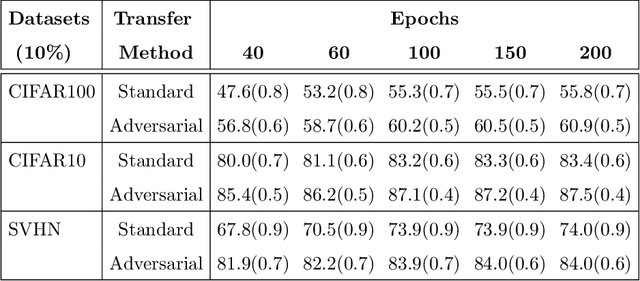
Certain datasets contain a limited number of samples with highly various styles and complex structures. This study presents a novel adversarial Lagrangian integrated contrastive embedding (ALICE) method for small-sized datasets. First, the accuracy improvement and training convergence of the proposed pre-trained adversarial transfer are shown on various subsets of datasets with few samples. Second, a novel adversarial integrated contrastive model using various augmentation techniques is investigated. The proposed structure considers the input samples with different appearances and generates a superior representation with adversarial transfer contrastive training. Finally, multi-objective augmented Lagrangian multipliers encourage the low-rank and sparsity of the presented adversarial contrastive embedding to adaptively estimate the coefficients of the regularizers automatically to the optimum weights. The sparsity constraint suppresses less representative elements in the feature space. The low-rank constraint eliminates trivial and redundant components and enables superior generalization. The performance of the proposed model is verified by conducting ablation studies by using benchmark datasets for scenarios with small data samples.

Object Type Clustering using Markov Directly-Follow Multigraph in Object-Centric Process Mining

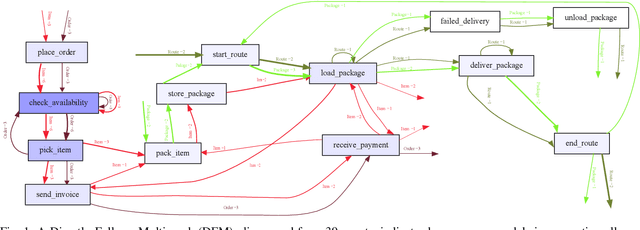
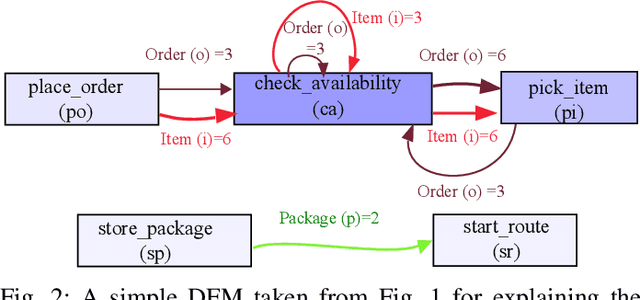
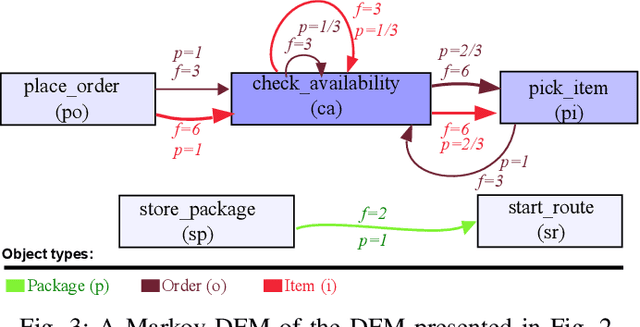
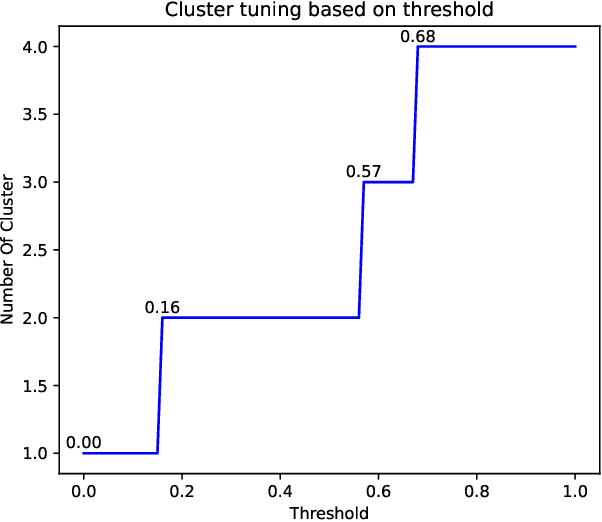
Object-centric process mining is a new paradigm with more realistic assumptions about underlying data by considering several case notions, e.g., an order handling process can be analyzed based on order, item, package, and route case notions. Including many case notions can result in a very complex model. To cope with such complexity, this paper introduces a new approach to cluster similar case notions based on Markov Directly-Follow Multigraph, which is an extended version of the well-known Directly-Follow Graph supported by many industrial and academic process mining tools. This graph is used to calculate a similarity matrix for discovering clusters of similar case notions based on a threshold. A threshold tuning algorithm is also defined to identify sets of different clusters that can be discovered based on different levels of similarity. Thus, the cluster discovery will not rely on merely analysts' assumptions. The approach is implemented and released as a part of a python library, called processmining, and it is evaluated through a Purchase to Pay (P2P) object-centric event log file. Some discovered clusters are evaluated by discovering Directly Follow-Multigraph by flattening the log based on the clusters. The similarity between identified clusters is also evaluated by calculating the similarity between the behavior of the process models discovered for each case notion using inductive miner based on footprints conformance checking.

Evaluating Perceived Usefulness and Ease of Use of CMMN and DCR

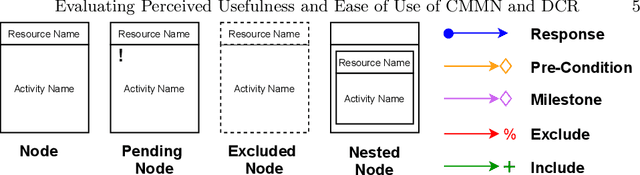
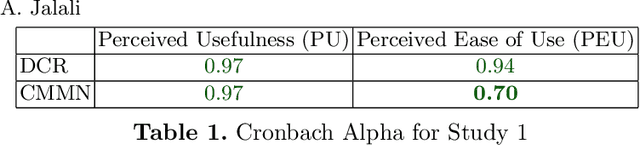
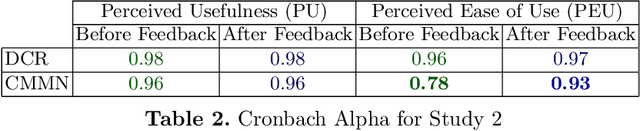
Case Management has been gradually evolving to support Knowledge-intensive business process management, which resulted in developing different modeling languages, e.g., Declare, Dynamic Condition Response (DCR), and Case Management Model and Notation (CMMN). A language will die if users do not accept and use it in practice - similar to extinct human languages. Thus, it is important to evaluate how users perceive languages to determine if there is a need for improvement. Although some studies have investigated how the process designers perceived Declare and DCR, there is a lack of research on how they perceive CMMN. Therefore, this study investigates how the process designers perceive the usefulness and ease of use of CMMN and DCR based on the Technology Acceptance Model. DCR is included to enable comparing the study result with previous ones. The study is performed by educating master level students with these languages over eight weeks by giving feedback on their assignments to reduce perceptions biases. The students' perceptions are collected through questionnaires before and after sending feedback on their final practice in the exam. Thus, the result shows how the perception of participants can change by receiving feedback - despite being well trained. The reliability of responses is tested using Cronbach's alpha, and the result indicates that both languages have an acceptable level for both perceived usefulness and ease of use.