Persistent Reductions in Regularized Loss Minimization for Variable Selection
Paper and Code
Nov 30, 2020
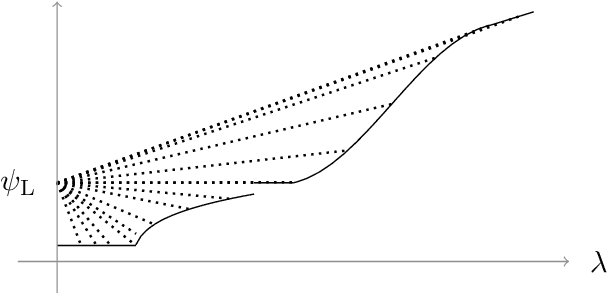
In the context of regularized loss minimization with polyhedral gauges, we show that for a broad class of loss functions (possibly non-smooth and non-convex) and under a simple geometric condition on the input data it is possible to efficiently identify a subset of features which are guaranteed to have zero coefficients in all optimal solutions in all problems with loss functions from said class, before any iterative optimization has been performed for the original problem. This procedure is standalone, takes only the data as input, and does not require any calls to the loss function. Therefore, we term this procedure as a persistent reduction for the aforementioned class of regularized loss minimization problems. This reduction can be efficiently implemented via an extreme ray identification subroutine applied to a polyhedral cone formed from the datapoints. We employ an existing output-sensitive algorithm for extreme ray identification which makes our guarantee and algorithm applicable in ultra-high dimensional problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge