Relative Density and Exact Recovery in Heterogeneous Stochastic Block Models
Paper and Code
Dec 15, 2015
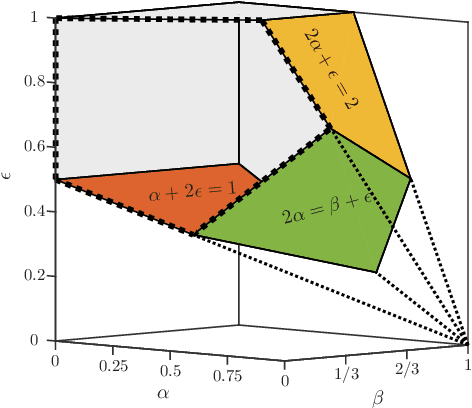
The Stochastic Block Model (SBM) is a widely used random graph model for networks with communities. Despite the recent burst of interest in recovering communities in the SBM from statistical and computational points of view, there are still gaps in understanding the fundamental information theoretic and computational limits of recovery. In this paper, we consider the SBM in its full generality, where there is no restriction on the number and sizes of communities or how they grow with the number of nodes, as well as on the connection probabilities inside or across communities. This generality allows us to move past the artifacts of homogenous SBM, and understand the right parameters (such as the relative densities of communities) that define the various recovery thresholds. We outline the implications of our generalizations via a set of illustrative examples. For instance, $\log n$ is considered to be the standard lower bound on the cluster size for exact recovery via convex methods, for homogenous SBM. We show that it is possible, in the right circumstances (when sizes are spread and the smaller the cluster, the denser), to recover very small clusters (up to $\sqrt{\log n}$ size), if there are just a few of them (at most polylogarithmic in $n$).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge