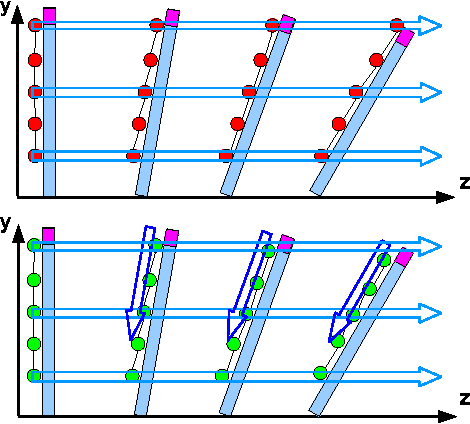
"Golden Ratio Yoshimura" for Meta-Stable and Massively Reconfigurable Deployment

Yoshimura origami is a classical folding pattern that has inspired many deployable structure designs. Its applications span from space exploration, kinetic architectures, and soft robots to even everyday household items. However, despite its wide usage, Yoshimura has been fixated on a set of design constraints to ensure its flat-foldability. Through extensive kinematic analysis and prototype tests, this study presents a new Yoshimura that intentionally defies these constraints. Remarkably, one can impart a unique meta-stability by using the Golden Ratio angle to define the triangular facets of a generalized Yoshimura. As a result, when its facets are strategically popped out, a ``Golden Ratio Yoshimura'' boom with $m$ modules can be theoretically reconfigured into $8^m$ geometrically unique and load-bearing shapes. This result not only challenges the existing design norms but also opens up a new avenue to create deployable and versatile structural systems.

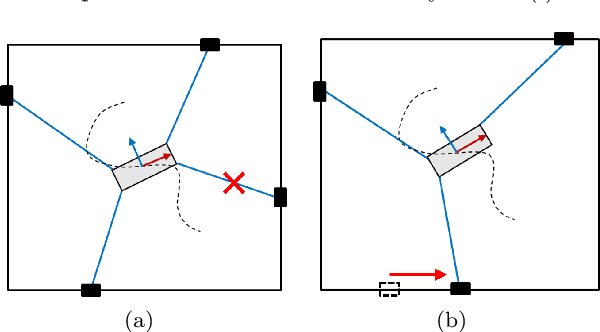
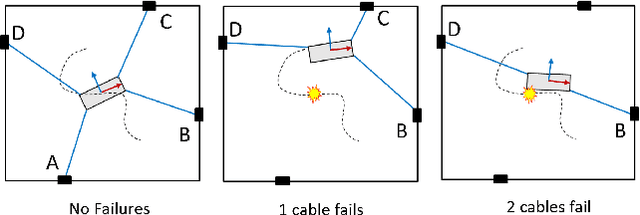
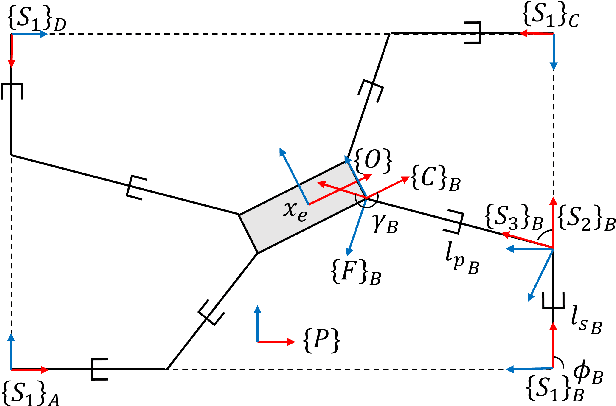
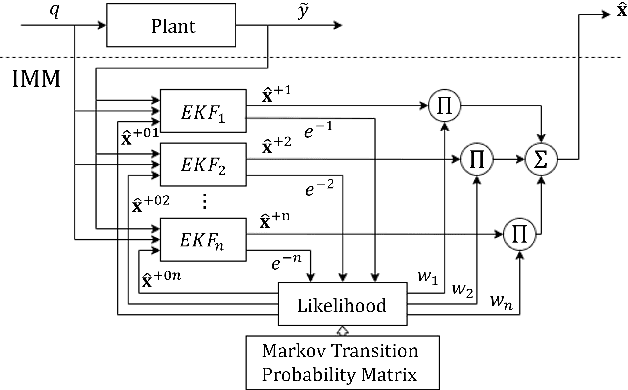
A Failure Identification and Recovery Framework for a Planar Reconfigurable Cable Driven Parallel Robot

In cable driven parallel robots (CDPRs), a single cable malfunction usually induces complete failure of the entire robot. However, the lost static workspace (due to failure) can often be recovered through reconfiguration of the cable attachment points on the frame. This capability is introduced by adding kinematic redundancies to the robot in the form of moving linear sliders that are manipulated in a real-time redundancy resolution controller. The presented work combines this controller with an online failure detection framework to develop a complete fault tolerant control scheme for automatic task recovery. This solution provides robustness by combining pose estimation of the end-effector with the failure detection through the application of an Interactive Multiple Model (IMM) algorithm relying only on end-effector information. The failure and pose estimation scheme is then tied into the redundancy resolution approach to produce a seamless automatic task (trajectory) recovery approach for cable failures.

Causality matters in medical imaging

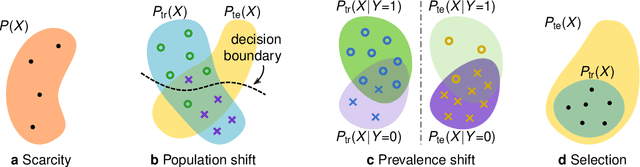
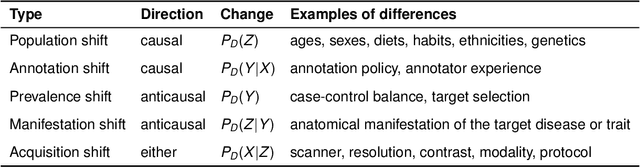
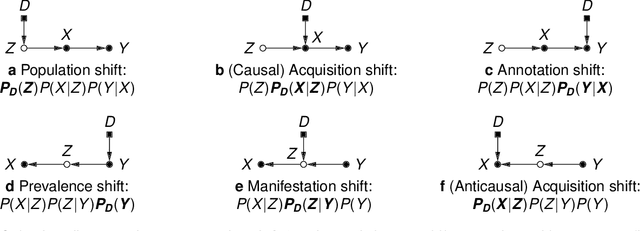
This article discusses how the language of causality can shed new light on the major challenges in machine learning for medical imaging: 1) data scarcity, which is the limited availability of high-quality annotations, and 2) data mismatch, whereby a trained algorithm may fail to generalize in clinical practice. Looking at these challenges through the lens of causality allows decisions about data collection, annotation procedures, and learning strategies to be made (and scrutinized) more transparently. We discuss how causal relationships between images and annotations can not only have profound effects on the performance of predictive models, but may even dictate which learning strategies should be considered in the first place. For example, we conclude that semi-supervision may be unsuitable for image segmentation---one of the possibly surprising insights from our causal analysis, which is illustrated with representative real-world examples of computer-aided diagnosis (skin lesion classification in dermatology) and radiotherapy (automated contouring of tumours). We highlight that being aware of and accounting for the causal relationships in medical imaging data is important for the safe development of machine learning and essential for regulation and responsible reporting. To facilitate this we provide step-by-step recommendations for future studies.

Graph Convolutional Gaussian Processes

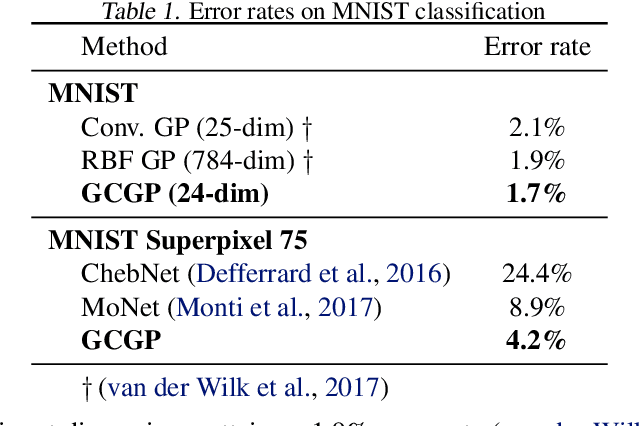
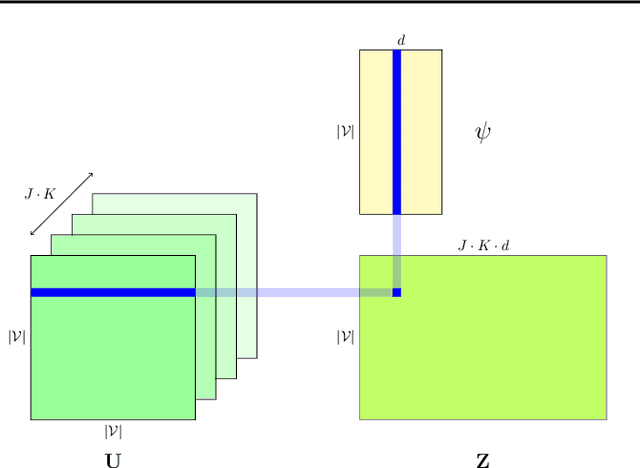
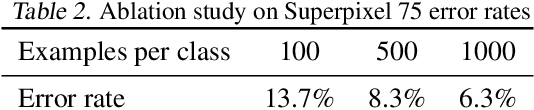
We propose a novel Bayesian nonparametric method to learn translation-invariant relationships on non-Euclidean domains. The resulting graph convolutional Gaussian processes can be applied to problems in machine learning for which the input observations are functions with domains on general graphs. The structure of these models allows for high dimensional inputs while retaining expressibility, as is the case with convolutional neural networks. We present applications of graph convolutional Gaussian processes to images and triangular meshes, demonstrating their versatility and effectiveness, comparing favorably to existing methods, despite being relatively simple models.

Semi-Supervised Learning via Compact Latent Space Clustering

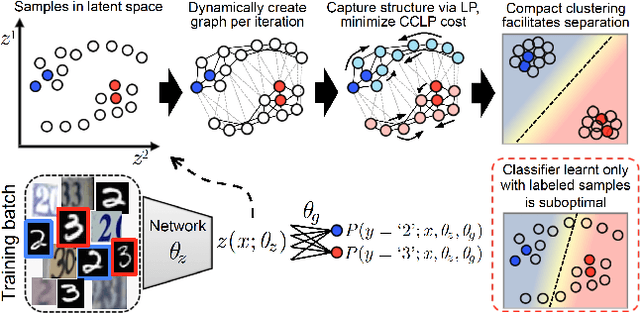
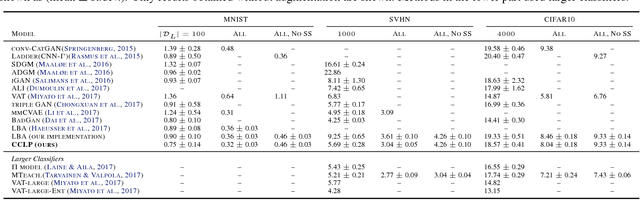
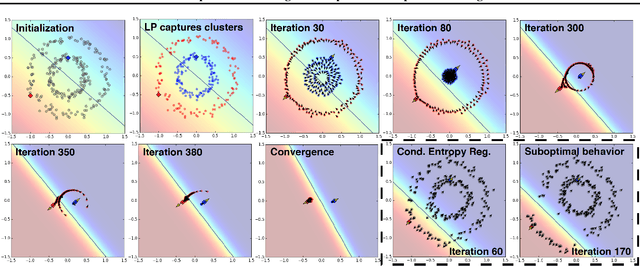
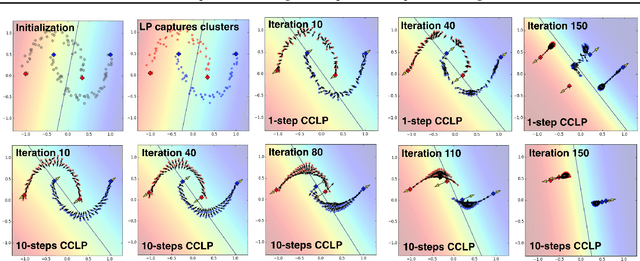
We present a novel cost function for semi-supervised learning of neural networks that encourages compact clustering of the latent space to facilitate separation. The key idea is to dynamically create a graph over embeddings of labeled and unlabeled samples of a training batch to capture underlying structure in feature space, and use label propagation to estimate its high and low density regions. We then devise a cost function based on Markov chains on the graph that regularizes the latent space to form a single compact cluster per class, while avoiding to disturb existing clusters during optimization. We evaluate our approach on three benchmarks and compare to state-of-the art with promising results. Our approach combines the benefits of graph-based regularization with efficient, inductive inference, does not require modifications to a network architecture, and can thus be easily applied to existing networks to enable an effective use of unlabeled data.

An Energy Minimization Approach to 3D Non-Rigid Deformable Surface Estimation Using RGBD Data

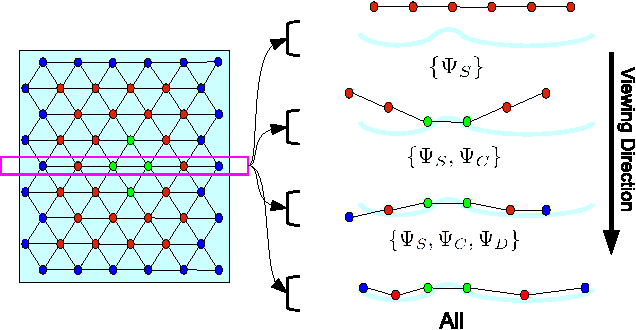
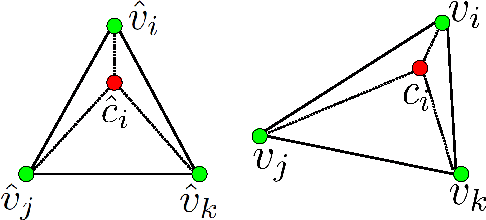
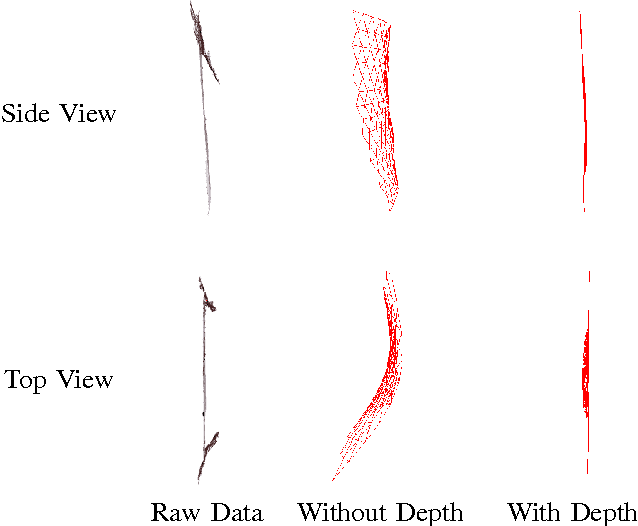
We propose an algorithm that uses energy mini- mization to estimate the current configuration of a non-rigid object. Our approach utilizes an RGBD image to calculate corresponding SURF features, depth, and boundary informa- tion. We do not use predetermined features, thus enabling our system to operate on unmodified objects. Our approach relies on a 3D nonlinear energy minimization framework to solve for the configuration using a semi-implicit scheme. Results show various scenarios of dynamic posters and shirts in different configurations to illustrate the performance of the method. In particular, we show that our method is able to estimate the configuration of a textureless nonrigid object with no correspondences available.