Non-Adversarial Inverse Reinforcement Learning via Successor Feature Matching

In inverse reinforcement learning (IRL), an agent seeks to replicate expert demonstrations through interactions with the environment. Traditionally, IRL is treated as an adversarial game, where an adversary searches over reward models, and a learner optimizes the reward through repeated RL procedures. This game-solving approach is both computationally expensive and difficult to stabilize. In this work, we propose a novel approach to IRL by direct policy optimization: exploiting a linear factorization of the return as the inner product of successor features and a reward vector, we design an IRL algorithm by policy gradient descent on the gap between the learner and expert features. Our non-adversarial method does not require learning a reward function and can be solved seamlessly with existing actor-critic RL algorithms. Remarkably, our approach works in state-only settings without expert action labels, a setting which behavior cloning (BC) cannot solve. Empirical results demonstrate that our method learns from as few as a single expert demonstration and achieves improved performance on various control tasks.

Action Gaps and Advantages in Continuous-Time Distributional Reinforcement Learning

When decisions are made at high frequency, traditional reinforcement learning (RL) methods struggle to accurately estimate action values. In turn, their performance is inconsistent and often poor. Whether the performance of distributional RL (DRL) agents suffers similarly, however, is unknown. In this work, we establish that DRL agents are sensitive to the decision frequency. We prove that action-conditioned return distributions collapse to their underlying policy's return distribution as the decision frequency increases. We quantify the rate of collapse of these return distributions and exhibit that their statistics collapse at different rates. Moreover, we define distributional perspectives on action gaps and advantages. In particular, we introduce the superiority as a probabilistic generalization of the advantage -- the core object of approaches to mitigating performance issues in high-frequency value-based RL. In addition, we build a superiority-based DRL algorithm. Through simulations in an option-trading domain, we validate that proper modeling of the superiority distribution produces improved controllers at high decision frequencies.

Foundations of Multivariate Distributional Reinforcement Learning

In reinforcement learning (RL), the consideration of multivariate reward signals has led to fundamental advancements in multi-objective decision-making, transfer learning, and representation learning. This work introduces the first oracle-free and computationally-tractable algorithms for provably convergent multivariate distributional dynamic programming and temporal difference learning. Our convergence rates match the familiar rates in the scalar reward setting, and additionally provide new insights into the fidelity of approximate return distribution representations as a function of the reward dimension. Surprisingly, when the reward dimension is larger than $1$, we show that standard analysis of categorical TD learning fails, which we resolve with a novel projection onto the space of mass-$1$ signed measures. Finally, with the aid of our technical results and simulations, we identify tradeoffs between distribution representations that influence the performance of multivariate distributional RL in practice.

A Distributional Analogue to the Successor Representation

This paper contributes a new approach for distributional reinforcement learning which elucidates a clean separation of transition structure and reward in the learning process. Analogous to how the successor representation (SR) describes the expected consequences of behaving according to a given policy, our distributional successor measure (SM) describes the distributional consequences of this behaviour. We formulate the distributional SM as a distribution over distributions and provide theory connecting it with distributional and model-based reinforcement learning. Moreover, we propose an algorithm that learns the distributional SM from data by minimizing a two-level maximum mean discrepancy. Key to our method are a number of algorithmic techniques that are independently valuable for learning generative models of state. As an illustration of the usefulness of the distributional SM, we show that it enables zero-shot risk-sensitive policy evaluation in a way that was not previously possible.

Policy Optimization in a Noisy Neighborhood: On Return Landscapes in Continuous Control

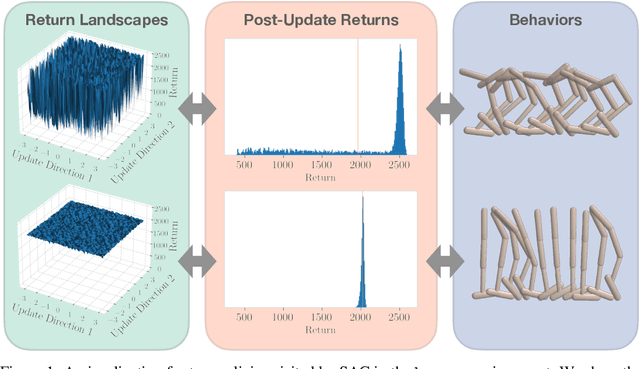
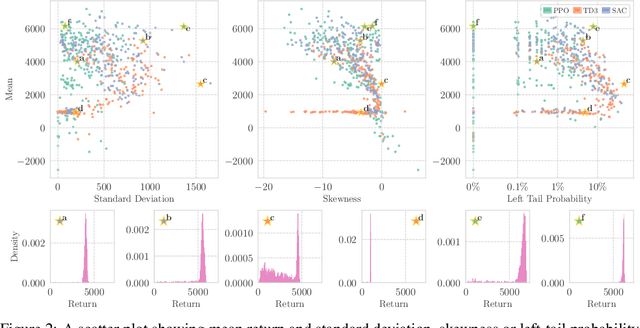
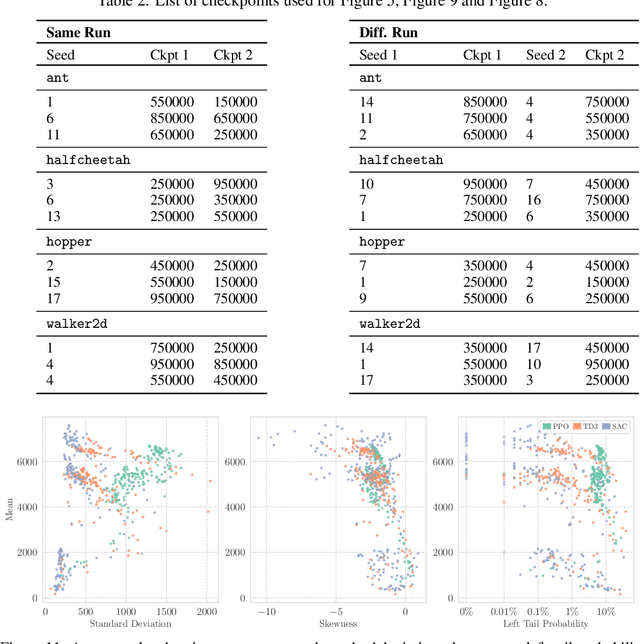
Deep reinforcement learning agents for continuous control are known to exhibit significant instability in their performance over time. In this work, we provide a fresh perspective on these behaviors by studying the return landscape: the mapping between a policy and a return. We find that popular algorithms traverse noisy neighborhoods of this landscape, in which a single update to the policy parameters leads to a wide range of returns. By taking a distributional view of these returns, we map the landscape, characterizing failure-prone regions of policy space and revealing a hidden dimension of policy quality. We show that the landscape exhibits surprising structure by finding simple paths in parameter space which improve the stability of a policy. To conclude, we develop a distribution-aware procedure which finds such paths, navigating away from noisy neighborhoods in order to improve the robustness of a policy. Taken together, our results provide new insight into the optimization, evaluation, and design of agents.

Distributional Hamilton-Jacobi-Bellman Equations for Continuous-Time Reinforcement Learning

Continuous-time reinforcement learning offers an appealing formalism for describing control problems in which the passage of time is not naturally divided into discrete increments. Here we consider the problem of predicting the distribution of returns obtained by an agent interacting in a continuous-time, stochastic environment. Accurate return predictions have proven useful for determining optimal policies for risk-sensitive control, learning state representations, multiagent coordination, and more. We begin by establishing the distributional analogue of the Hamilton-Jacobi-Bellman (HJB) equation for It\^o diffusions and the broader class of Feller-Dynkin processes. We then specialize this equation to the setting in which the return distribution is approximated by $N$ uniformly-weighted particles, a common design choice in distributional algorithms. Our derivation highlights additional terms due to statistical diffusivity which arise from the proper handling of distributions in the continuous-time setting. Based on this, we propose a tractable algorithm for approximately solving the distributional HJB based on a JKO scheme, which can be implemented in an online control algorithm. We demonstrate the effectiveness of such an algorithm in a synthetic control problem.