RankUp: Towards High-rank Representations for Large Scale Advertising Recommender Systems

The scaling laws for recommender systems have been increasingly validated, where MetaFormer-based architectures consistently benefit from increased model depth, hidden dimensionality, and user behavior sequence length. However, whether representation capacity scales proportionally with parameter growth remains largely unexplored. Prior studies on RankMixer reveal that the effective rank of token representations exhibits a damped oscillatory trajectory across layers, failing to increase consistently with depth and even degrading in deeper layers. Motivated by this observation, we propose \textbf{RankUp}, an architecture designed to mitigate representation collapse and enhance expressive capacity through randomized permutation splitting over sparse features, a multi-embedding paradigm, global token integration, crossed pretrained embedding tokens and task-specific token decoupling. RankUp has been fully deployed in large-scale production across Weixin Video Accounts, Official Accounts and Moments, yielding GMV improvements of 3.41\%, 4.81\% and 2.21\%, respectively.

TokenFormer: Unify the Multi-Field and Sequential Recommendation Worlds

Recommender systems have historically developed along two largely independent paradigms: feature interaction models for modeling correlations among multi-field categorical features, and sequential models for capturing user behavior dynamics from historical interaction sequences. Although recent trends attempt to bridge these paradigms within shared backbones, we empirically reveal that naive unifying these two branches may lead to a failure mode of Sequential Collapse Propagation (SCP). That is, the interaction with those dimensionally ill non-sequence fields leads to the dimensional collapse of the sequence features. To overcome this challenge, we propose TokenFormer, a unified recommendation architecture with the following innovations. First, we introduce a Bottom-Full-Top-Sliding (BFTS) attention scheme, which applies full self-attention in the lower layers and shrinking-window sliding attention in the upper layers. Second, we introduce a Non-Linear Interaction Representation (NLIR) that applies one-sided non-linear multiplicative transformations to the hidden states. Extensive experiments on public benchmarks and Tencent's advertising platform demonstrate state-of-the-art performance, while detailed analysis confirm that TokenFormer significantly improves dimensional robustness and representation discriminability under unified modeling.

Tencent Advertising Algorithm Challenge 2025: All-Modality Generative Recommendation

Generative recommender systems are rapidly emerging as a new paradigm for recommendation, where collaborative identifiers and/or multi-modal content are mapped into discrete token spaces and user behavior is modelled with autoregressive sequence models. Despite progress on multi-modal recommendation datasets, there is still a lack of public benchmarks that jointly offer large-scale, realistic and fully all-modality data designed specifically for generative recommendation (GR) in industrial advertising. To foster research in this direction, we organised the Tencent Advertising Algorithm Challenge 2025, a global competition built on top of two all-modality datasets for GR: TencentGR-1M and TencentGR-10M. Both datasets are constructed from real de-identified Tencent Ads logs and contain rich collaborative IDs and multi-modal representations extracted with state-of-the-art embedding models. The preliminary track (TencentGR-1M) provides 1 million user sequences with up to 100 interacted items each, where each interaction is labeled with exposure and click signals, while the final track (TencentGR-10M) scales this to 10 million users and explicitly distinguishes between click and conversion events at both the sequence and target level. This paper presents the task definition, data construction process, feature schema, baseline GR model, evaluation protocol, and key findings from top-ranked and award-winning solutions. Our datasets focus on multi-modal sequence generation in an advertising setting and introduce weighted evaluation for high-value conversion events. We release our datasets at https://huggingface.co/datasets/TAAC2025 and baseline implementations at https://github.com/TencentAdvertisingAlgorithmCompetition/baseline_2025 to enable future research on all-modality generative recommendation at an industrial scale. The official website is https://algo.qq.com/2025.

Large Foundation Model for Ads Recommendation

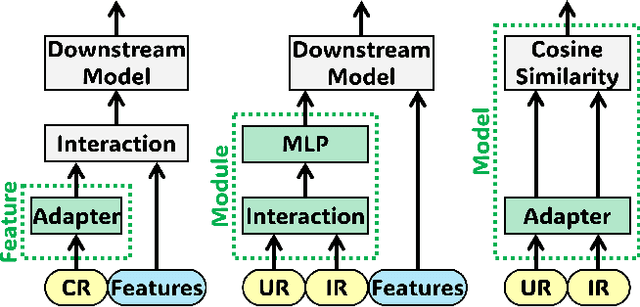
Online advertising relies on accurate recommendation models, with recent advances using pre-trained large-scale foundation models (LFMs) to capture users' general interests across multiple scenarios and tasks. However, existing methods have critical limitations: they extract and transfer only user representations (URs), ignoring valuable item representations (IRs) and user-item cross representations (CRs); and they simply use a UR as a feature in downstream applications, which fails to bridge upstream-downstream gaps and overlooks more transfer granularities. In this paper, we propose LFM4Ads, an All-Representation Multi-Granularity transfer framework for ads recommendation. It first comprehensively transfers URs, IRs, and CRs, i.e., all available representations in the pre-trained foundation model. To effectively utilize the CRs, it identifies the optimal extraction layer and aggregates them into transferable coarse-grained forms. Furthermore, we enhance the transferability via multi-granularity mechanisms: non-linear adapters for feature-level transfer, an Isomorphic Interaction Module for module-level transfer, and Standalone Retrieval for model-level transfer. LFM4Ads has been successfully deployed in Tencent's industrial-scale advertising platform, processing tens of billions of daily samples while maintaining terabyte-scale model parameters with billions of sparse embedding keys across approximately two thousand features. Since its production deployment in Q4 2024, LFM4Ads has achieved 10+ successful production launches across various advertising scenarios, including primary ones like Weixin Moments and Channels. These launches achieve an overall GMV lift of 2.45% across the entire platform, translating to estimated annual revenue increases in the hundreds of millions of dollars.

LEADRE: Multi-Faceted Knowledge Enhanced LLM Empowered Display Advertisement Recommender System

Display advertising provides significant value to advertisers, publishers, and users. Traditional display advertising systems utilize a multi-stage architecture consisting of retrieval, coarse ranking, and final ranking. However, conventional retrieval methods rely on ID-based learning to rank mechanisms and fail to adequately utilize the content information of ads, which hampers their ability to provide diverse recommendation lists. To address this limitation, we propose leveraging the extensive world knowledge of LLMs. However, three key challenges arise when attempting to maximize the effectiveness of LLMs: "How to capture user interests", "How to bridge the knowledge gap between LLMs and advertising system", and "How to efficiently deploy LLMs". To overcome these challenges, we introduce a novel LLM-based framework called LLM Empowered Display ADvertisement REcommender system (LEADRE). LEADRE consists of three core modules: (1) The Intent-Aware Prompt Engineering introduces multi-faceted knowledge and designs intent-aware <Prompt, Response> pairs that fine-tune LLMs to generate ads tailored to users' personal interests. (2) The Advertising-Specific Knowledge Alignment incorporates auxiliary fine-tuning tasks and Direct Preference Optimization (DPO) to align LLMs with ad semantic and business value. (3) The Efficient System Deployment deploys LEADRE in an online environment by integrating both latency-tolerant and latency-sensitive service. Extensive offline experiments demonstrate the effectiveness of LEADRE and validate the contributions of individual modules. Online A/B test shows that LEADRE leads to a 1.57% and 1.17% GMV lift for serviced users on WeChat Channels and Moments separately. LEADRE has been deployed on both platforms, serving tens of billions of requests each day.

AdaScale SGD: A User-Friendly Algorithm for Distributed Training

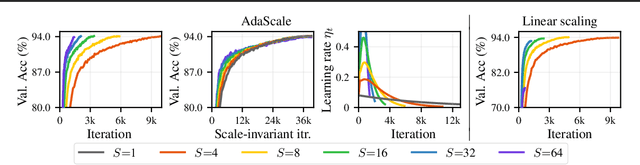
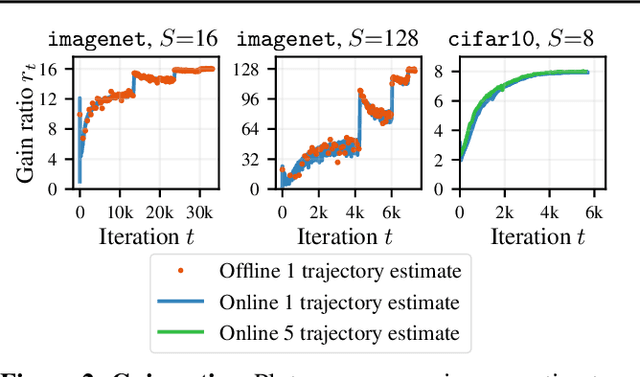
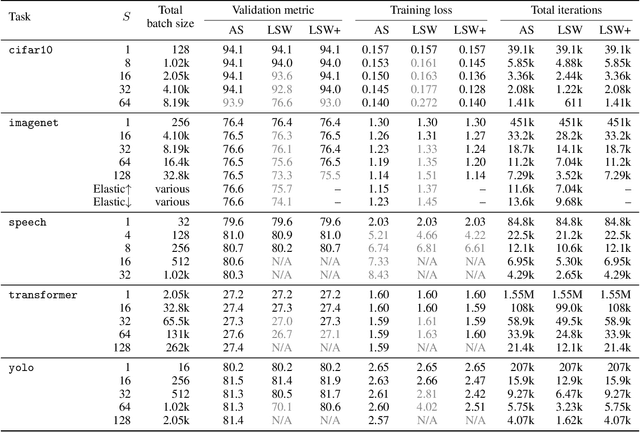
When using large-batch training to speed up stochastic gradient descent, learning rates must adapt to new batch sizes in order to maximize speed-ups and preserve model quality. Re-tuning learning rates is resource intensive, while fixed scaling rules often degrade model quality. We propose AdaScale SGD, an algorithm that reliably adapts learning rates to large-batch training. By continually adapting to the gradient's variance, AdaScale automatically achieves speed-ups for a wide range of batch sizes. We formally describe this quality with AdaScale's convergence bound, which maintains final objective values, even as batch sizes grow large and the number of iterations decreases. In empirical comparisons, AdaScale trains well beyond the batch size limits of popular "linear learning rate scaling" rules. This includes large-batch training with no model degradation for machine translation, image classification, object detection, and speech recognition tasks. AdaScale's qualitative behavior is similar to that of "warm-up" heuristics, but unlike warm-up, this behavior emerges naturally from a principled mechanism. The algorithm introduces negligible computational overhead and no new hyperparameters, making AdaScale an attractive choice for large-scale training in practice.

Sequential Nonparametric Regression

We present algorithms for nonparametric regression in settings where the data are obtained sequentially. While traditional estimators select bandwidths that depend upon the sample size, for sequential data the effective sample size is dynamically changing. We propose a linear time algorithm that adjusts the bandwidth for each new data point, and show that the estimator achieves the optimal minimax rate of convergence. We also propose the use of online expert mixing algorithms to adapt to unknown smoothness of the regression function. We provide simulations that confirm the theoretical results, and demonstrate the effectiveness of the methods.

Forest Density Estimation

We study graph estimation and density estimation in high dimensions, using a family of density estimators based on forest structured undirected graphical models. For density estimation, we do not assume the true distribution corresponds to a forest; rather, we form kernel density estimates of the bivariate and univariate marginals, and apply Kruskal's algorithm to estimate the optimal forest on held out data. We prove an oracle inequality on the excess risk of the resulting estimator relative to the risk of the best forest. For graph estimation, we consider the problem of estimating forests with restricted tree sizes. We prove that finding a maximum weight spanning forest with restricted tree size is NP-hard, and develop an approximation algorithm for this problem. Viewing the tree size as a complexity parameter, we then select a forest using data splitting, and prove bounds on excess risk and structure selection consistency of the procedure. Experiments with simulated data and microarray data indicate that the methods are a practical alternative to Gaussian graphical models.