Nonlinear Sparse Generalized Canonical Correlation Analysis for Multi-view High-dimensional Data

Motivation: Biomedical studies increasingly produce multi-view high-dimensional datasets (e.g., multi-omics) that demand integrative analysis. Existing canonical correlation analysis (CCA) and generalized CCA methods address at most two of the following three key aspects simultaneously: (i) nonlinear dependence, (ii) sparsity for variable selection, and (iii) generalization to more than two data views. There is a pressing need for CCA methods that integrate all three aspects to effectively analyze multi-view high-dimensional data. Results: We propose three nonlinear, sparse, generalized CCA methods, HSIC-SGCCA, SA-KGCCA, and TS-KGCCA, for variable selection in multi-view high-dimensional data. These methods extend existing SCCA-HSIC, SA-KCCA, and TS-KCCA from two-view to multi-view settings. While SA-KGCCA and TS-KGCCA yield multi-convex optimization problems solved via block coordinate descent, HSIC-SGCCA introduces a necessary unit-variance constraint previously ignored in SCCA-HSIC, resulting in a nonconvex, non-multiconvex problem. We efficiently address this challenge by integrating the block prox-linear method with the linearized alternating direction method of multipliers. Simulations and TCGA-BRCA data analysis demonstrate that HSIC-SGCCA outperforms competing methods in multi-view variable selection.

Conditional Diffusion Models Based Conditional Independence Testing

Conditional independence (CI) testing is a fundamental task in modern statistics and machine learning. The conditional randomization test (CRT) was recently introduced to test whether two random variables, $X$ and $Y$, are conditionally independent given a potentially high-dimensional set of random variables, $Z$. The CRT operates exceptionally well under the assumption that the conditional distribution $X|Z$ is known. However, since this distribution is typically unknown in practice, accurately approximating it becomes crucial. In this paper, we propose using conditional diffusion models (CDMs) to learn the distribution of $X|Z$. Theoretically and empirically, it is shown that CDMs closely approximate the true conditional distribution. Furthermore, CDMs offer a more accurate approximation of $X|Z$ compared to GANs, potentially leading to a CRT that performs better than those based on GANs. To accommodate complex dependency structures, we utilize a computationally efficient classifier-based conditional mutual information (CMI) estimator as our test statistic. The proposed testing procedure performs effectively without requiring assumptions about specific distribution forms or feature dependencies, and is capable of handling mixed-type conditioning sets that include both continuous and discrete variables. Theoretical analysis shows that our proposed test achieves a valid control of the type I error. A series of experiments on synthetic data demonstrates that our new test effectively controls both type-I and type-II errors, even in high dimensional scenarios.

Enhancing Missing Data Imputation through Combined Bipartite Graph and Complete Directed Graph

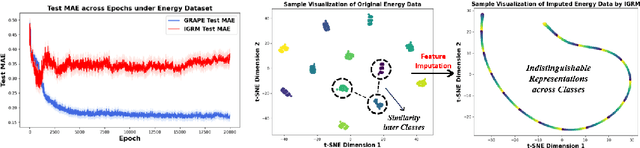
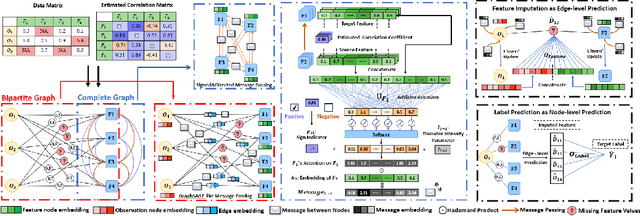
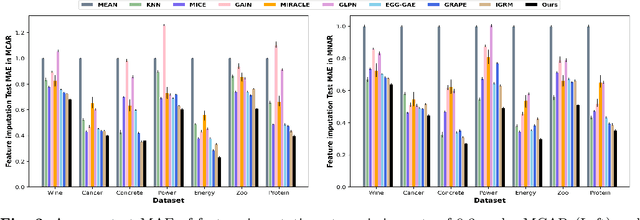
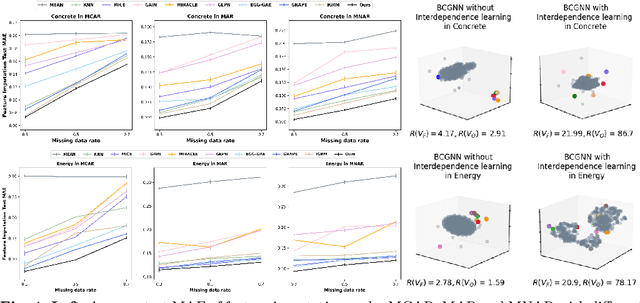
In this paper, we aim to address a significant challenge in the field of missing data imputation: identifying and leveraging the interdependencies among features to enhance missing data imputation for tabular data. We introduce a novel framework named the Bipartite and Complete Directed Graph Neural Network (BCGNN). Within BCGNN, observations and features are differentiated as two distinct node types, and the values of observed features are converted into attributed edges linking them. The bipartite segment of our framework inductively learns embedding representations for nodes, efficiently utilizing the comprehensive information encapsulated in the attributed edges. In parallel, the complete directed graph segment adeptly outlines and communicates the complex interdependencies among features. When compared to contemporary leading imputation methodologies, BCGNN consistently outperforms them, achieving a noteworthy average reduction of 15% in mean absolute error for feature imputation tasks under different missing mechanisms. Our extensive experimental investigation confirms that an in-depth grasp of the interdependence structure substantially enhances the model's feature embedding ability. We also highlight the model's superior performance in label prediction tasks involving missing data, and its formidable ability to generalize to unseen data points.

3D U-KAN Implementation for Multi-modal MRI Brain Tumor Segmentation

We explore the application of U-KAN, a U-Net based network enhanced with Kolmogorov-Arnold Network (KAN) layers, for 3D brain tumor segmentation using multi-modal MRI data. We adapt the original 2D U-KAN model to the 3D task, and introduce a variant called UKAN-SE, which incorporates Squeeze-and-Excitation modules for global attention. We compare the performance of U-KAN and UKAN-SE against existing methods such as U-Net, Attention U-Net, and Swin UNETR, using the BraTS 2024 dataset. Our results show that U-KAN and UKAN-SE, with approximately 10.6 million parameters, achieve exceptional efficiency, requiring only about 1/4 of the training time of U-Net and Attention U-Net, and 1/6 that of Swin UNETR, while surpassing these models across most evaluation metrics. Notably, UKAN-SE slightly outperforms U-KAN.

D-CDLF: Decomposition of Common and Distinctive Latent Factors for Multi-view High-dimensional Data

A typical approach to the joint analysis of multiple high-dimensional data views is to decompose each view's data matrix into three parts: a low-rank common-source matrix generated by common latent factors of all data views, a low-rank distinctive-source matrix generated by distinctive latent factors of the corresponding data view, and an additive noise matrix. Existing decomposition methods often focus on the uncorrelatedness between the common latent factors and distinctive latent factors, but inadequately address the equally necessary uncorrelatedness between distinctive latent factors from different data views. We propose a novel decomposition method, called Decomposition of Common and Distinctive Latent Factors (D-CDLF), to effectively achieve both types of uncorrelatedness for two-view data. We also discuss the estimation of the D-CDLF under high-dimensional settings.

DeepFDR: A Deep Learning-based False Discovery Rate Control Method for Neuroimaging Data

Voxel-based multiple testing is widely used in neuroimaging data analysis. Traditional false discovery rate (FDR) control methods often ignore the spatial dependence among the voxel-based tests and thus suffer from substantial loss of testing power. While recent spatial FDR control methods have emerged, their validity and optimality remain questionable when handling the complex spatial dependencies of the brain. Concurrently, deep learning methods have revolutionized image segmentation, a task closely related to voxel-based multiple testing. In this paper, we propose DeepFDR, a novel spatial FDR control method that leverages unsupervised deep learning-based image segmentation to address the voxel-based multiple testing problem. Numerical studies, including comprehensive simulations and Alzheimer's disease FDG-PET image analysis, demonstrate DeepFDR's superiority over existing methods. DeepFDR not only excels in FDR control and effectively diminishes the false nondiscovery rate, but also boasts exceptional computational efficiency highly suited for tackling large-scale neuroimaging data.

Structure-consistent Restoration Network for Cataract Fundus Image Enhancement

Fundus photography is a routine examination in clinics to diagnose and monitor ocular diseases. However, for cataract patients, the fundus image always suffers quality degradation caused by the clouding lens. The degradation prevents reliable diagnosis by ophthalmologists or computer-aided systems. To improve the certainty in clinical diagnosis, restoration algorithms have been proposed to enhance the quality of fundus images. Unfortunately, challenges remain in the deployment of these algorithms, such as collecting sufficient training data and preserving retinal structures. In this paper, to circumvent the strict deployment requirement, a structure-consistent restoration network (SCR-Net) for cataract fundus images is developed from synthesized data that shares an identical structure. A cataract simulation model is firstly designed to collect synthesized cataract sets (SCS) formed by cataract fundus images sharing identical structures. Then high-frequency components (HFCs) are extracted from the SCS to constrain structure consistency such that the structure preservation in SCR-Net is enforced. The experiments demonstrate the effectiveness of SCR-Net in the comparison with state-of-the-art methods and the follow-up clinical applications. The code is available at https://github.com/liamheng/ArcNet-Medical-Image-Enhancement.

A comparative study of non-deep learning, deep learning, and ensemble learning methods for sunspot number prediction

Solar activity has significant impacts on human activities and health. One most commonly used measure of solar activity is the sunspot number. This paper compares three important non-deep learning models, four popular deep learning models, and their five ensemble models in forecasting sunspot numbers. Our proposed ensemble model XGBoost-DL, which uses XGBoost as a two-level nonlinear ensemble method to combine the deep learning models, achieves the best forecasting performance among all considered models and the NASA's forecast. Our XGBoost-DL forecasts a peak sunspot number of 133.47 in May 2025 for Solar Cycle 25 and 164.62 in November 2035 for Solar Cycle 26, similar to but later than the NASA's at 137.7 in October 2024 and 161.2 in December 2034.

BiTr-Unet: a CNN-Transformer Combined Network for MRI Brain Tumor Segmentation

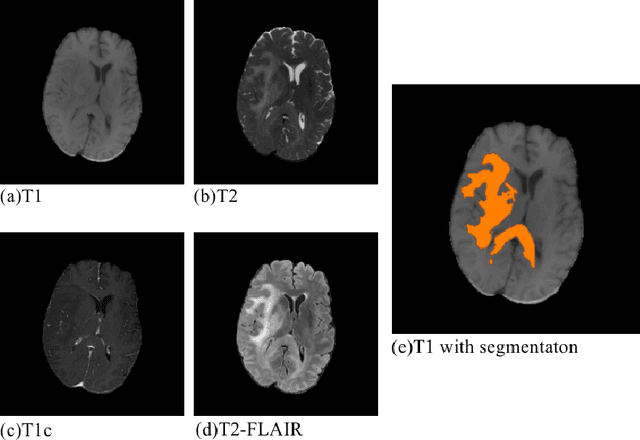
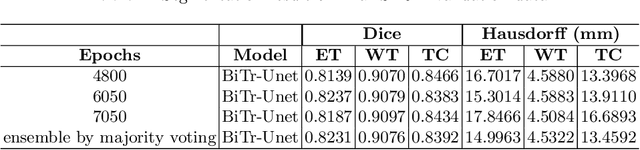
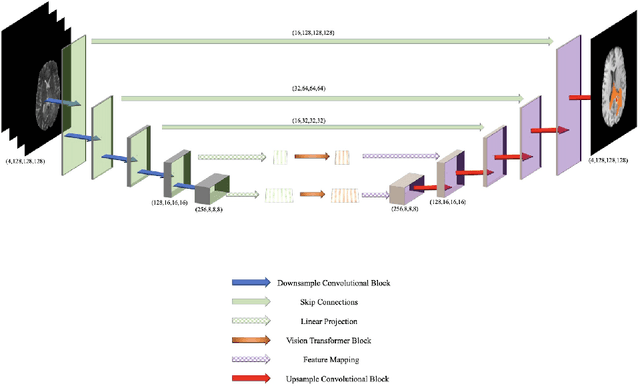
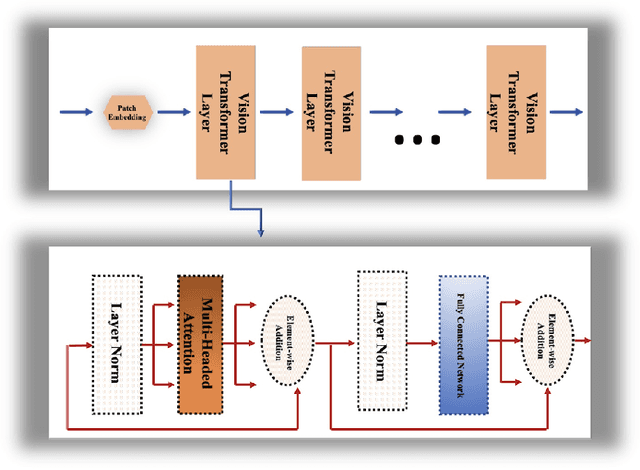
Convolutional neural networks (CNNs) have recently achieved remarkable success in automatically identifying organs or lesions on 3D medical images. Meanwhile, vision transformer networks have exhibited exceptional performance in 2D image classification tasks. Compared with CNNs, transformer networks have an obvious advantage of extracting long-range features due to their self-attention algorithm. Therefore, in this paper we present a CNN-Transformer combined model called BiTr-Unet for brain tumor segmentation on multi-modal MRI scans. The proposed BiTr-Unet achieves good performance on the BraTS 2021 validation dataset with mean Dice score 0.9076, 0.8392 and 0.8231, and mean Hausdorff distance 4.5322, 13.4592 and 14.9963 for the whole tumor, tumor core, and enhancing tumor, respectively.

A Two-Stage Cascade Model with Variational Autoencoders and Attention Gates for MRI Brain Tumor Segmentation

Automatic MRI brain tumor segmentation is of vital importance for the disease diagnosis, monitoring, and treatment planning. In this paper, we propose a two-stage encoder-decoder based model for brain tumor subregional segmentation. Variational autoencoder regularization is utilized in both stages to prevent the overfitting issue. The second-stage network adopts attention gates and is trained additionally using an expanded dataset formed by the first-stage outputs. On the BraTS 2020 validation dataset, the proposed method achieves the mean Dice score of 0.9041, 0.8350, and 0.7958, and Hausdorff distance (95%) of 4.953, 6.299, and 23.608 for the whole tumor, tumor core, and enhancing tumor, respectively. The corresponding results on the BraTS 2020 testing dataset are 0.8729, 0.8357, and 0.8205 for Dice score, and 11.4288, 19.9690, and 15.6711 for Hausdorff distance.