Projection Abstractions in Planning Under the Lenses of Abstractions for MDPs

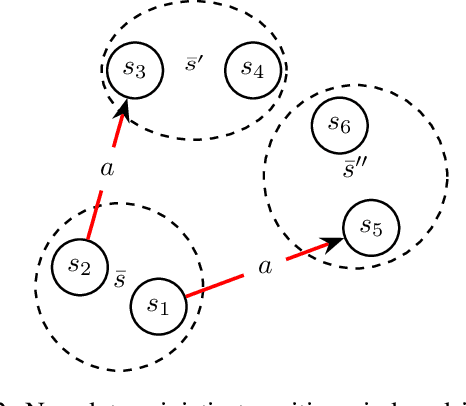
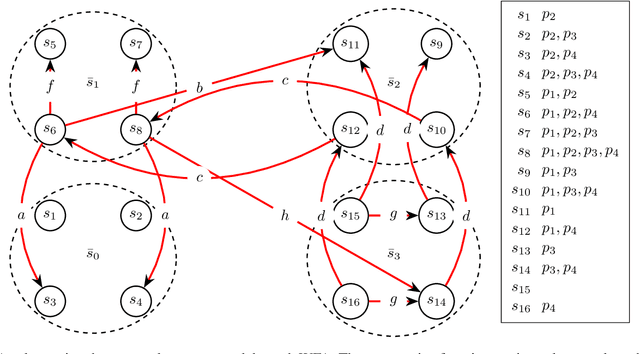
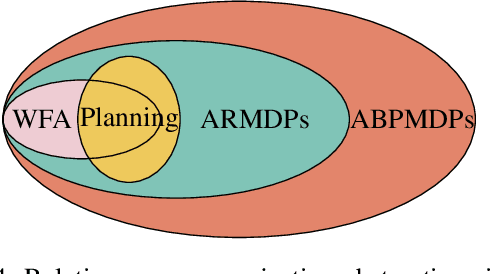
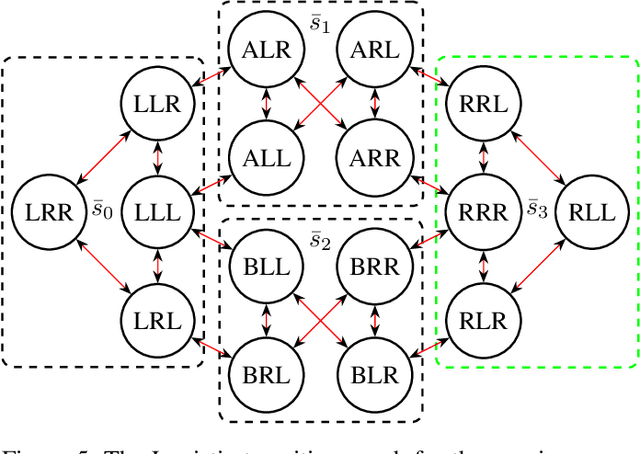
The concept of abstraction has been independently developed both in the context of AI Planning and discounted Markov Decision Processes (MDPs). However, the way abstractions are built and used in the context of Planning and MDPs is different even though lots of commonalities can be highlighted. To this day there is no work trying to relate and unify the two fields on the matter of abstractions unraveling all the different assumptions and their effect on the way they can be used. Therefore, in this paper we aim to do so by looking at projection abstractions in Planning through the lenses of discounted MDPs. Starting from a projection abstraction built according to Classical or Probabilistic Planning techniques, we will show how the same abstraction can be obtained under the abstraction frameworks available for discounted MDPs. Along the way, we will focus on computational as well as representational advantages and disadvantages of both worlds pointing out new research directions that are of interest for both fields.

On Learning Action Costs from Input Plans

Most of the work on learning action models focus on learning the actions' dynamics from input plans. This allows us to specify the valid plans of a planning task. However, very little work focuses on learning action costs, which in turn allows us to rank the different plans. In this paper we introduce a new problem: that of learning the costs of a set of actions such that a set of input plans are optimal under the resulting planning model. To solve this problem we present $LACFIP^k$, an algorithm to learn action's costs from unlabeled input plans. We provide theoretical and empirical results showing how $LACFIP^k$ can successfully solve this task.

On the Sample Efficiency of Abstractions and Potential-Based Reward Shaping in Reinforcement Learning

The use of Potential Based Reward Shaping (PBRS) has shown great promise in the ongoing research effort to tackle sample inefficiency in Reinforcement Learning (RL). However, the choice of the potential function is critical for this technique to be effective. Additionally, RL techniques are usually constrained to use a finite horizon for computational limitations. This introduces a bias when using PBRS, thus adding an additional layer of complexity. In this paper, we leverage abstractions to automatically produce a "good" potential function. We analyse the bias induced by finite horizons in the context of PBRS producing novel insights. Finally, to asses sample efficiency and performance impact, we evaluate our approach on four environments including a goal-oriented navigation task and three Arcade Learning Environments (ALE) games demonstrating that we can reach the same level of performance as CNN-based solutions with a simple fully-connected network.

Time-Variant Variational Transfer for Value Functions

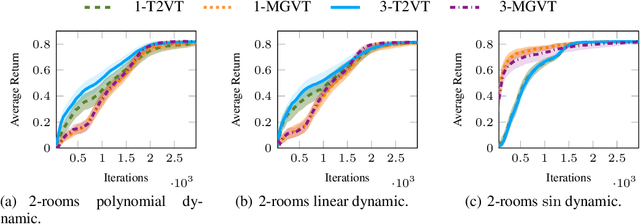
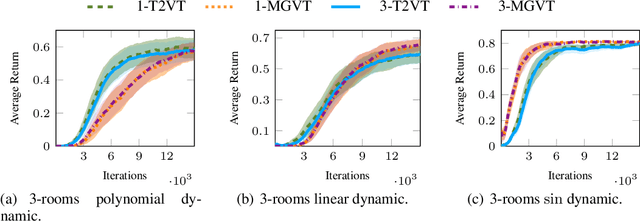
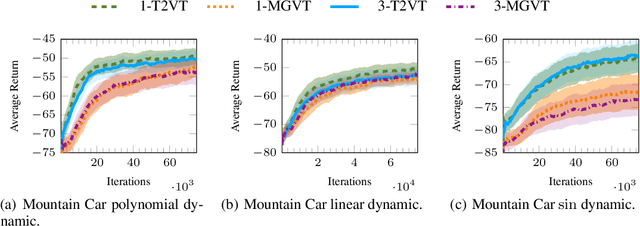
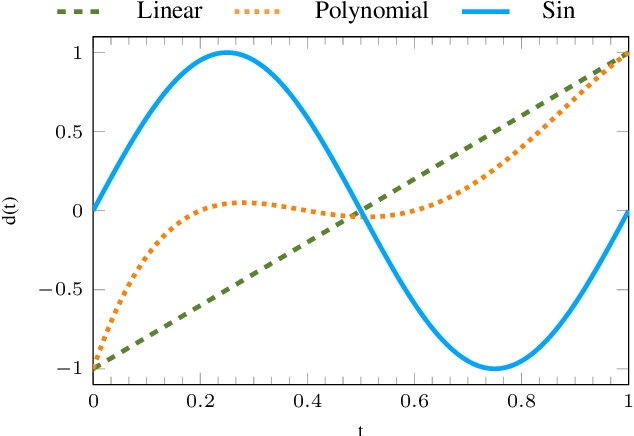
In most of the transfer learning approaches to reinforcement learning (RL) the distribution over the tasks is assumed to be stationary. Therefore, the target and source tasks are i.i.d. samples of the same distribution. In the context of this work, we consider the problem of transferring value functions through a variational method when the distribution that generates the tasks is time-variant, proposing a solution that leverages this temporal structure inherent in the task generating process. Furthermore, by means of a finite-sample analysis, the previously mentioned solution is theoretically compared to its time-invariant version. Finally, we will provide an experimental evaluation of the proposed technique with three distinct temporal dynamics in three different RL environments.

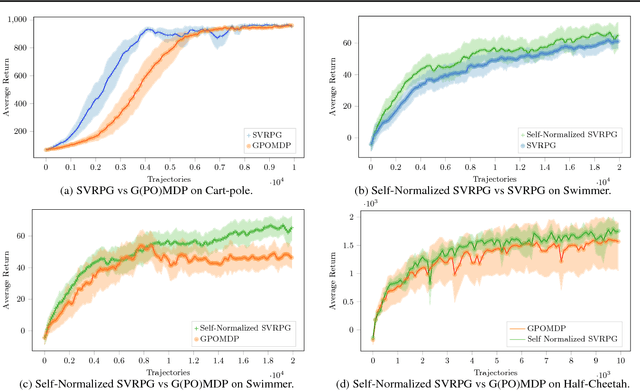
Stochastic Variance-Reduced Policy Gradient

In this paper, we propose a novel reinforcement- learning algorithm consisting in a stochastic variance-reduced version of policy gradient for solving Markov Decision Processes (MDPs). Stochastic variance-reduced gradient (SVRG) methods have proven to be very successful in supervised learning. However, their adaptation to policy gradient is not straightforward and needs to account for I) a non-concave objective func- tion; II) approximations in the full gradient com- putation; and III) a non-stationary sampling pro- cess. The result is SVRPG, a stochastic variance- reduced policy gradient algorithm that leverages on importance weights to preserve the unbiased- ness of the gradient estimate. Under standard as- sumptions on the MDP, we provide convergence guarantees for SVRPG with a convergence rate that is linear under increasing batch sizes. Finally, we suggest practical variants of SVRPG, and we empirically evaluate them on continuous MDPs.