Gael Varoquaux
topic group 6 of the STRATOS initiative
Performance evaluation of predictive AI models to support medical decisions: Overview and guidance
Dec 13, 2024
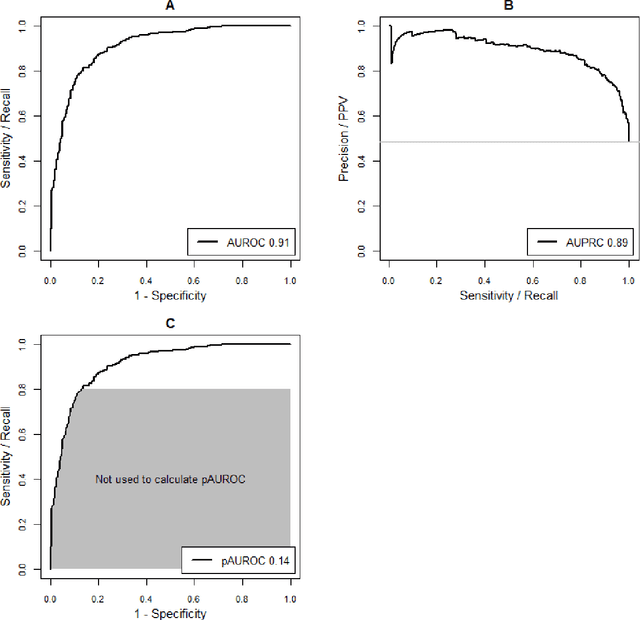
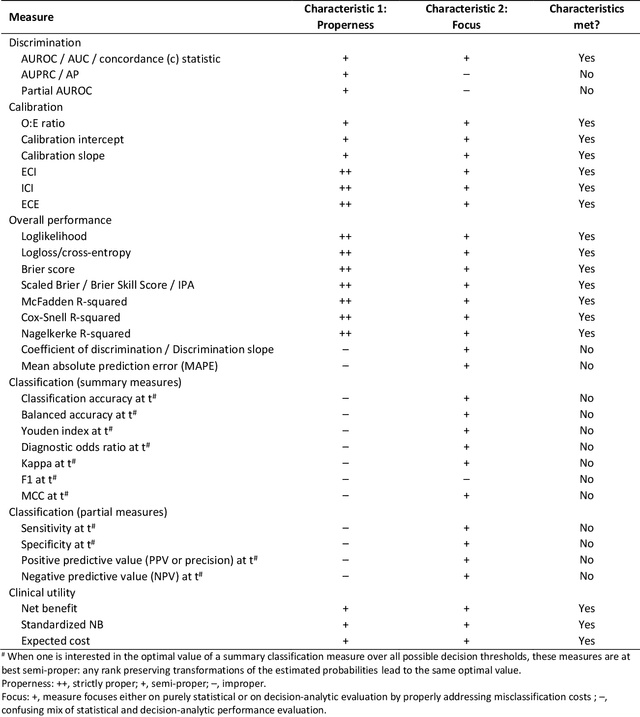
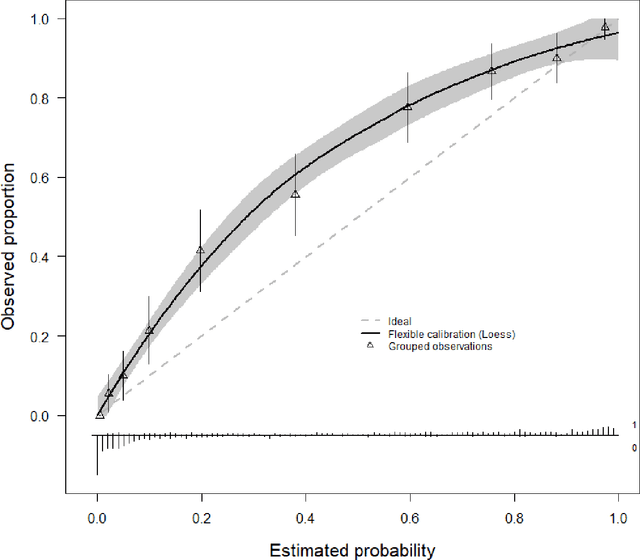
Abstract:A myriad of measures to illustrate performance of predictive artificial intelligence (AI) models have been proposed in the literature. Selecting appropriate performance measures is essential for predictive AI models that are developed to be used in medical practice, because poorly performing models may harm patients and lead to increased costs. We aim to assess the merits of classic and contemporary performance measures when validating predictive AI models for use in medical practice. We focus on models with a binary outcome. We discuss 32 performance measures covering five performance domains (discrimination, calibration, overall, classification, and clinical utility) along with accompanying graphical assessments. The first four domains cover statistical performance, the fifth domain covers decision-analytic performance. We explain why two key characteristics are important when selecting which performance measures to assess: (1) whether the measure's expected value is optimized when it is calculated using the correct probabilities (i.e., a "proper" measure), and (2) whether they reflect either purely statistical performance or decision-analytic performance by properly considering misclassification costs. Seventeen measures exhibit both characteristics, fourteen measures exhibited one characteristic, and one measure possessed neither characteristic (the F1 measure). All classification measures (such as classification accuracy and F1) are improper for clinically relevant decision thresholds other than 0.5 or the prevalence. We recommend the following measures and plots as essential to report: AUROC, calibration plot, a clinical utility measure such as net benefit with decision curve analysis, and a plot with probability distributions per outcome category.
Retrieve, Merge, Predict: Augmenting Tables with Data Lakes
Feb 13, 2024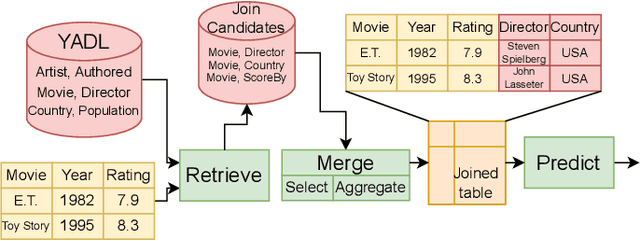
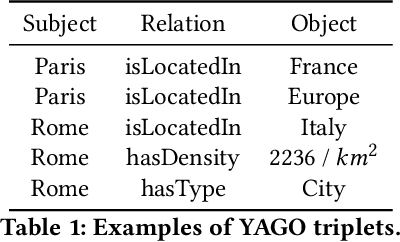

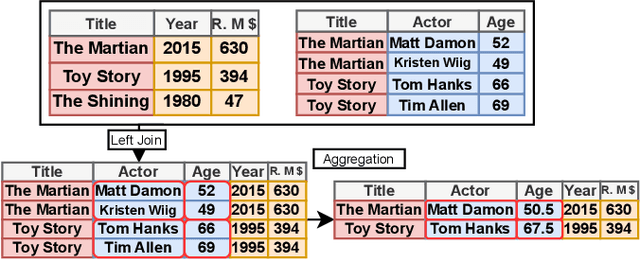
Abstract:We present an in-depth analysis of data discovery in data lakes, focusing on table augmentation for given machine learning tasks. We analyze alternative methods used in the three main steps: retrieving joinable tables, merging information, and predicting with the resultant table. As data lakes, the paper uses YADL (Yet Another Data Lake) -- a novel dataset we developed as a tool for benchmarking this data discovery task -- and Open Data US, a well-referenced real data lake. Through systematic exploration on both lakes, our study outlines the importance of accurately retrieving join candidates and the efficiency of simple merging methods. We report new insights on the benefits of existing solutions and on their limitations, aiming at guiding future research in this space.
Manifold-regression to predict from MEG/EEG brain signals without source modeling
Jun 07, 2019



Abstract:Magnetoencephalography and electroencephalography (M/EEG) can reveal neuronal dynamics non-invasively in real-time and are therefore appreciated methods in medicine and neuroscience. Recent advances in modeling brain-behavior relationships have highlighted the effectiveness of Riemannian geometry for summarizing the spatially correlated time-series from M/EEG in terms of their covariance. However, after artefact-suppression, M/EEG data is often rank deficient which limits the application of Riemannian concepts. In this article, we focus on the task of regression with rank-reduced covariance matrices. We study two Riemannian approaches that vectorize the M/EEG covariance between-sensors through projection into a tangent space. The Wasserstein distance readily applies to rank-reduced data but lacks affine-invariance. This can be overcome by finding a common subspace in which the covariance matrices are full rank, enabling the affine-invariant geometric distance. We investigated the implications of these two approaches in synthetic generative models, which allowed us to control estimation bias of a linear model for prediction. We show that Wasserstein and geometric distances allow perfect out-of-sample prediction on the generative models. We then evaluated the methods on real data with regard to their effectiveness in predicting age from M/EEG covariance matrices. The findings suggest that the data-driven Riemannian methods outperform different sensor-space estimators and that they get close to the performance of biophysics-driven source-localization model that requires MRI acquisitions and tedious data processing. Our study suggests that the proposed Riemannian methods can serve as fundamental building-blocks for automated large-scale analysis of M/EEG.
Computational and informatics advances for reproducible data analysis in neuroimaging
Sep 24, 2018



Abstract:The reproducibility of scientific research has become a point of critical concern. We argue that openness and transparency are critical for reproducibility, and we outline an ecosystem for open and transparent science that has emerged within the human neuroimaging community. We discuss the range of open data sharing resources that have been developed for neuroimaging data, and the role of data standards (particularly the Brain Imaging Data Structure) in enabling the automated sharing, processing, and reuse of large neuroimaging datasets. We outline how the open-source Python language has provided the basis for a data science platform that enables reproducible data analysis and visualization. We also discuss how new advances in software engineering, such as containerization, provide the basis for greater reproducibility in data analysis. The emergence of this new ecosystem provides an example for many areas of science that are currently struggling with reproducibility.
Using Feature Grouping as a Stochastic Regularizer for High-Dimensional Noisy Data
Jul 31, 2018



Abstract:The use of complex models --with many parameters-- is challenging with high-dimensional small-sample problems: indeed, they face rapid overfitting. Such situations are common when data collection is expensive, as in neuroscience, biology, or geology. Dedicated regularization can be crafted to tame overfit, typically via structured penalties. But rich penalties require mathematical expertise and entail large computational costs. Stochastic regularizers such as dropout are easier to implement: they prevent overfitting by random perturbations. Used inside a stochastic optimizer, they come with little additional cost. We propose a structured stochastic regularization that relies on feature grouping. Using a fast clustering algorithm, we define a family of groups of features that capture feature covariations. We then randomly select these groups inside a stochastic gradient descent loop. This procedure acts as a structured regularizer for high-dimensional correlated data without additional computational cost and it has a denoising effect. We demonstrate the performance of our approach for logistic regression both on a sample-limited face image dataset with varying additive noise and on a typical high-dimensional learning problem, brain image classification.
Stochastic Subsampling for Factorizing Huge Matrices
Oct 30, 2017



Abstract:We present a matrix-factorization algorithm that scales to input matrices with both huge number of rows and columns. Learned factors may be sparse or dense and/or non-negative, which makes our algorithm suitable for dictionary learning, sparse component analysis, and non-negative matrix factorization. Our algorithm streams matrix columns while subsampling them to iteratively learn the matrix factors. At each iteration, the row dimension of a new sample is reduced by subsampling, resulting in lower time complexity compared to a simple streaming algorithm. Our method comes with convergence guarantees to reach a stationary point of the matrix-factorization problem. We demonstrate its efficiency on massive functional Magnetic Resonance Imaging data (2 TB), and on patches extracted from hyperspectral images (103 GB). For both problems, which involve different penalties on rows and columns, we obtain significant speed-ups compared to state-of-the-art algorithms.
* IEEE Transactions on Signal Processing, Institute of Electrical and Electronics Engineers, A Para\^itre
Fast clustering for scalable statistical analysis on structured images
Nov 16, 2015
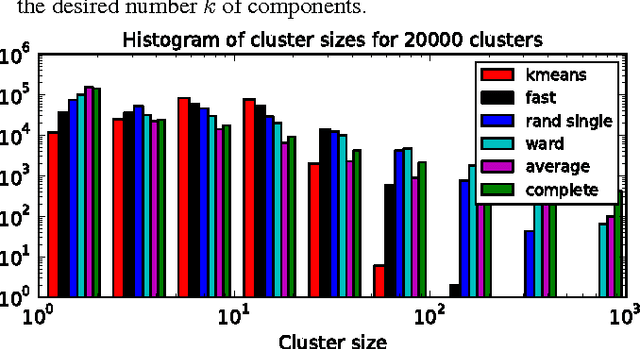
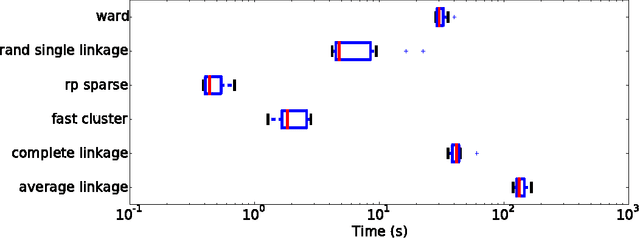
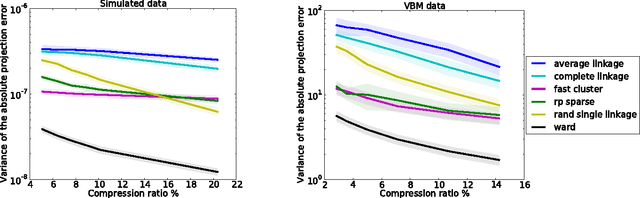
Abstract:The use of brain images as markers for diseases or behavioral differences is challenged by the small effects size and the ensuing lack of power, an issue that has incited researchers to rely more systematically on large cohorts. Coupled with resolution increases, this leads to very large datasets. A striking example in the case of brain imaging is that of the Human Connectome Project: 20 Terabytes of data and growing. The resulting data deluge poses severe challenges regarding the tractability of some processing steps (discriminant analysis, multivariate models) due to the memory demands posed by these data. In this work, we revisit dimension reduction approaches, such as random projections, with the aim of replacing costly function evaluations by cheaper ones while decreasing the memory requirements. Specifically, we investigate the use of alternate schemes, based on fast clustering, that are well suited for signals exhibiting a strong spatial structure, such as anatomical and functional brain images. Our contribution is twofold: i) we propose a linear-time clustering scheme that bypasses the percolation issues inherent in these algorithms and thus provides compressions nearly as good as traditional quadratic-complexity variance-minimizing clustering schemes, ii) we show that cluster-based compression can have the virtuous effect of removing high-frequency noise, actually improving subsequent estimations steps. As a consequence, the proposed approach yields very accurate models on several large-scale problems yet with impressive gains in computational efficiency, making it possible to analyze large datasets.
Region segmentation for sparse decompositions: better brain parcellations from rest fMRI
Dec 12, 2014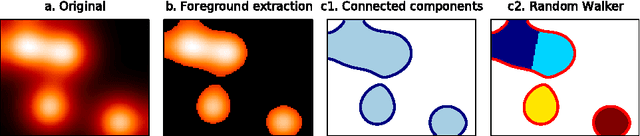
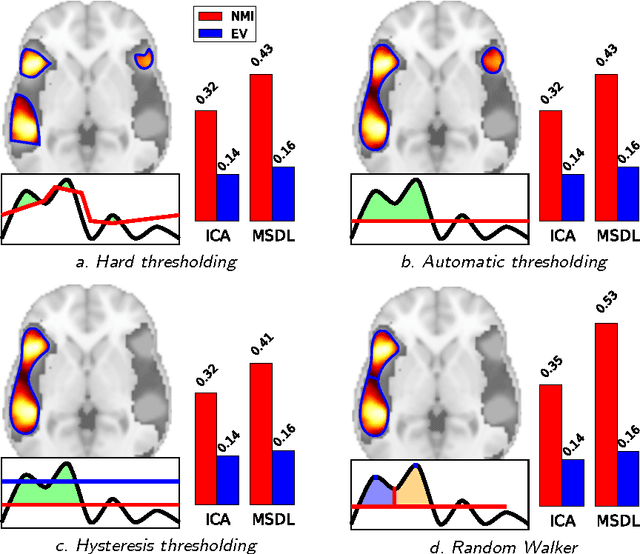
Abstract:Functional Magnetic Resonance Images acquired during resting-state provide information about the functional organization of the brain through measuring correlations between brain areas. Independent components analysis is the reference approach to estimate spatial components from weakly structured data such as brain signal time courses; each of these components may be referred to as a brain network and the whole set of components can be conceptualized as a brain functional atlas. Recently, new methods using a sparsity prior have emerged to deal with low signal-to-noise ratio data. However, even when using sophisticated priors, the results may not be very sparse and most often do not separate the spatial components into brain regions. This work presents post-processing techniques that automatically sparsify brain maps and separate regions properly using geometric operations, and compares these techniques according to faithfulness to data and stability metrics. In particular, among threshold-based approaches, hysteresis thresholding and random walker segmentation, the latter improves significantly the stability of both dense and sparse models.
Small-sample Brain Mapping: Sparse Recovery on Spatially Correlated Designs with Randomization and Clustering
Jun 27, 2012



Abstract:Functional neuroimaging can measure the brain?s response to an external stimulus. It is used to perform brain mapping: identifying from these observations the brain regions involved. This problem can be cast into a linear supervised learning task where the neuroimaging data are used as predictors for the stimulus. Brain mapping is then seen as a support recovery problem. On functional MRI (fMRI) data, this problem is particularly challenging as i) the number of samples is small due to limited acquisition time and ii) the variables are strongly correlated. We propose to overcome these difficulties using sparse regression models over new variables obtained by clustering of the original variables. The use of randomization techniques, e.g. bootstrap samples, and clustering of the variables improves the recovery properties of sparse methods. We demonstrate the benefit of our approach on an extensive simulation study as well as two fMRI datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge