Jonas Kahn
PARIETAL
Recursive nearest agglomeration (ReNA): fast clustering for approximation of structured signals
Mar 19, 2018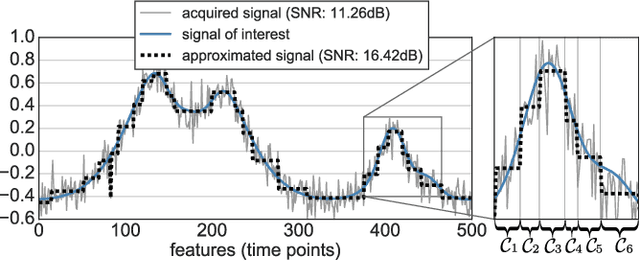
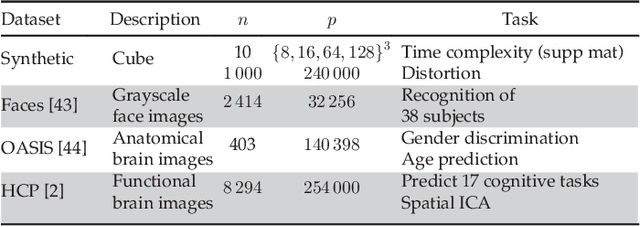
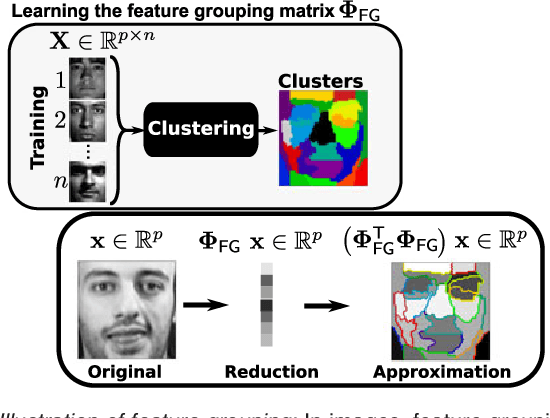
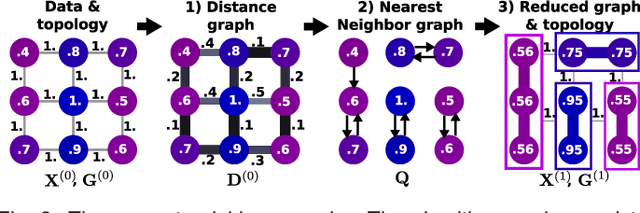
Abstract:In this work, we revisit fast dimension reduction approaches, as with random projections and random sampling. Our goal is to summarize the data to decrease computational costs and memory footprint of subsequent analysis. Such dimension reduction can be very efficient when the signals of interest have a strong structure, such as with images. We focus on this setting and investigate feature clustering schemes for data reductions that capture this structure. An impediment to fast dimension reduction is that good clustering comes with large algorithmic costs. We address it by contributing a linear-time agglomerative clustering scheme, Recursive Nearest Agglomeration (ReNA). Unlike existing fast agglomerative schemes, it avoids the creation of giant clusters. We empirically validate that it approximates the data as well as traditional variance-minimizing clustering schemes that have a quadratic complexity. In addition, we analyze signal approximation with feature clustering and show that it can remove noise, improving subsequent analysis steps. As a consequence, data reduction by clustering features with ReNA yields very fast and accurate models, enabling to process large datasets on budget. Our theoretical analysis is backed by extensive experiments on publicly-available data that illustrate the computation efficiency and the denoising properties of the resulting dimension reduction scheme.
Fast clustering for scalable statistical analysis on structured images
Nov 16, 2015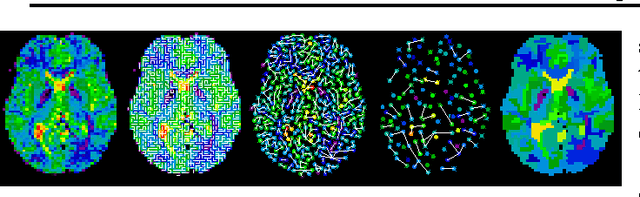
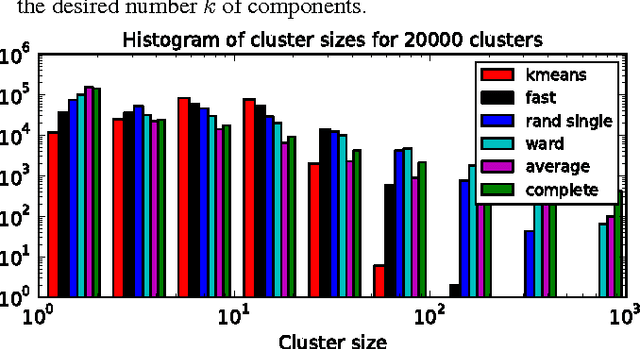
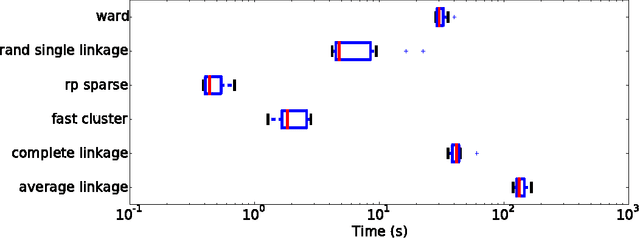
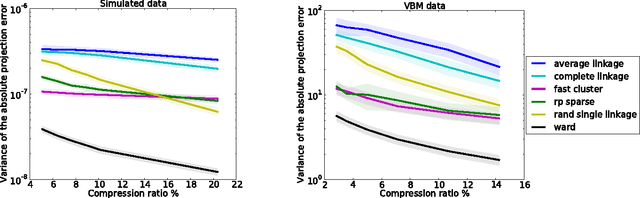
Abstract:The use of brain images as markers for diseases or behavioral differences is challenged by the small effects size and the ensuing lack of power, an issue that has incited researchers to rely more systematically on large cohorts. Coupled with resolution increases, this leads to very large datasets. A striking example in the case of brain imaging is that of the Human Connectome Project: 20 Terabytes of data and growing. The resulting data deluge poses severe challenges regarding the tractability of some processing steps (discriminant analysis, multivariate models) due to the memory demands posed by these data. In this work, we revisit dimension reduction approaches, such as random projections, with the aim of replacing costly function evaluations by cheaper ones while decreasing the memory requirements. Specifically, we investigate the use of alternate schemes, based on fast clustering, that are well suited for signals exhibiting a strong spatial structure, such as anatomical and functional brain images. Our contribution is twofold: i) we propose a linear-time clustering scheme that bypasses the percolation issues inherent in these algorithms and thus provides compressions nearly as good as traditional quadratic-complexity variance-minimizing clustering schemes, ii) we show that cluster-based compression can have the virtuous effect of removing high-frequency noise, actually improving subsequent estimations steps. As a consequence, the proposed approach yields very accurate models on several large-scale problems yet with impressive gains in computational efficiency, making it possible to analyze large datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge