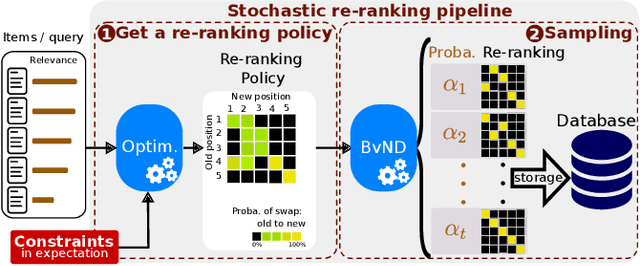
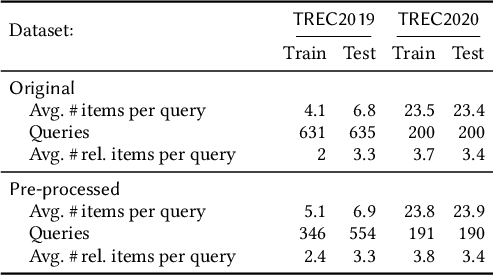
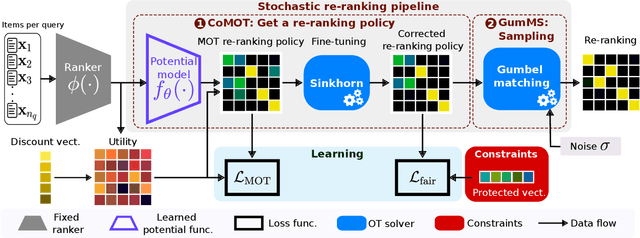
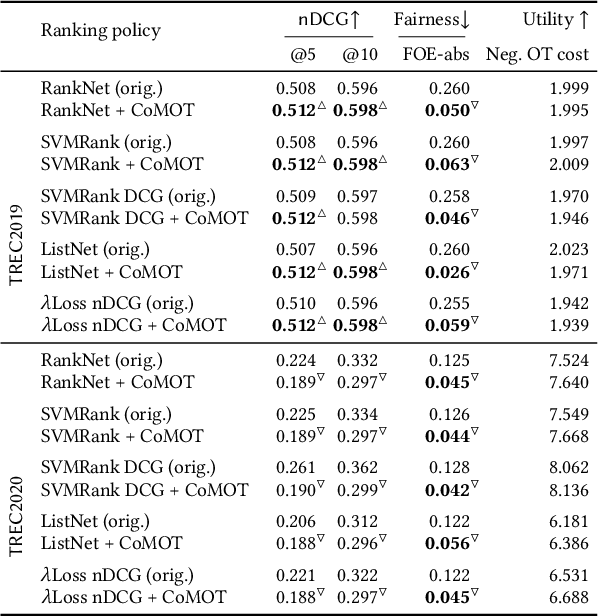
Learning to Re-rank with Constrained Meta-Optimal Transport

Many re-ranking strategies in search systems rely on stochastic ranking policies, encoded as Doubly-Stochastic (DS) matrices, that satisfy desired ranking constraints in expectation, e.g., Fairness of Exposure (FOE). These strategies are generally two-stage pipelines: \emph{i)} an offline re-ranking policy construction step and \emph{ii)} an online sampling of rankings step. Building a re-ranking policy requires repeatedly solving a constrained optimization problem, one for each issued query. Thus, it is necessary to recompute the optimization procedure for any new/unseen query. Regarding sampling, the Birkhoff-von-Neumann decomposition (BvND) is the favored approach to draw rankings from any DS-based policy. However, the BvND is too costly to compute online. Hence, the BvND as a sampling solution is memory-consuming as it can grow as $\gO(N\, n^2)$ for $N$ queries and $n$ documents. This paper offers a novel, fast, lightweight way to predict fair stochastic re-ranking policies: Constrained Meta-Optimal Transport (CoMOT). This method fits a neural network shared across queries like a learning-to-rank system. We also introduce Gumbel-Matching Sampling (GumMS), an online sampling approach from DS-based policies. Our proposed pipeline, CoMOT + GumMS, only needs to store the parameters of a single model, and it generalizes to unseen queries. We empirically evaluated our pipeline on the TREC 2019 and 2020 datasets under FOE constraints. Our experiments show that CoMOT rapidly predicts fair re-ranking policies on held-out data, with a speed-up proportional to the average number of documents per query. It also displays fairness and ranking performance similar to the original optimization-based policy. Furthermore, we empirically validate the effectiveness of GumMS to approximate DS-based policies in expectation.

Aligning Hyperbolic Representations: an Optimal Transport-based approach

Hyperbolic-spaces are better suited to represent data with underlying hierarchical relationships, e.g., tree-like data. However, it is often necessary to incorporate, through alignment, different but related representations meaningfully. This aligning is an important class of machine learning problems, with applications as ontology matching and cross-lingual alignment. Optimal transport (OT)-based approaches are a natural choice to tackle the alignment problem as they aim to find a transformation of the source dataset to match a target dataset, subject to some distribution constraints. This work proposes a novel approach based on OT of embeddings on the Poincar\'e model of hyperbolic spaces. Our method relies on the gyrobarycenter mapping on M\"obius gyrovector spaces. As a result of this formalism, we derive extensions to some existing Euclidean methods of OT-based domain adaptation to their hyperbolic counterparts. Empirically, we show that both Euclidean and hyperbolic methods have similar performances in the context of retrieval.

Local Bures-Wasserstein Transport: A Practical and Fast Mapping Approximation

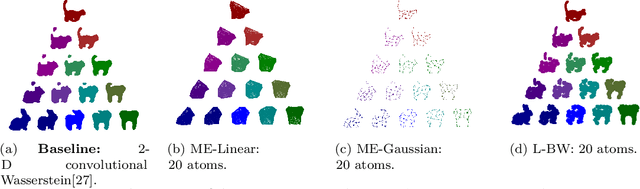
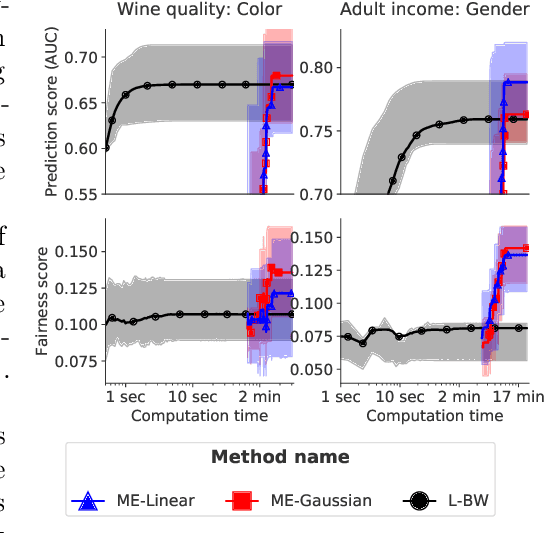
Optimal transport (OT)-based methods have a wide range of applications and have attracted a tremendous amount of attention in recent years. However, most of the computational approaches of OT do not learn the underlying transport map. Although some algorithms have been proposed to learn this map, they rely on kernel-based methods, which makes them prohibitively slow when the number of samples increases. Here, we propose a way to learn an approximate transport map and a parametric approximation of the Wasserstein barycenter. We build an approximated transport mapping by leveraging the closed-form of Gaussian (Bures-Wasserstein) transport; we compute local transport plans between matched pairs of the Gaussian components of each density. The learned map generalizes to out-of-sample examples. We provide experimental results on simulated and real data, comparing our proposed method with other mapping estimation algorithms. Preliminary experiments suggest that our proposed method is not only faster, with a factor 80 overall running time, but it also requires fewer components than state-of-the-art methods to recover the support of the barycenter. From a practical standpoint, it is straightforward to implement and can be used with a conventional machine learning pipeline.

Recursive nearest agglomeration (ReNA): fast clustering for approximation of structured signals

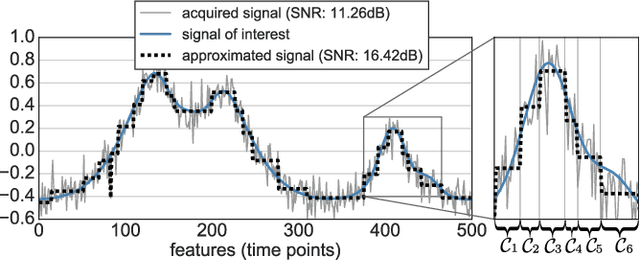
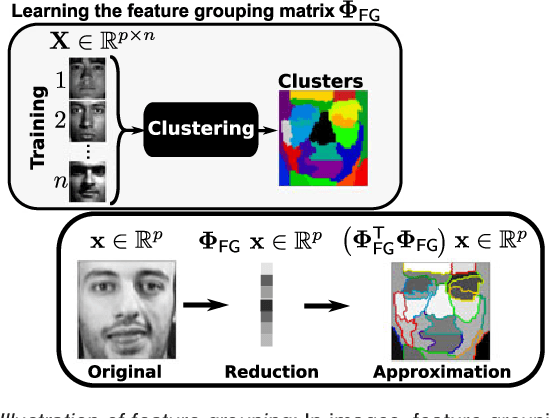
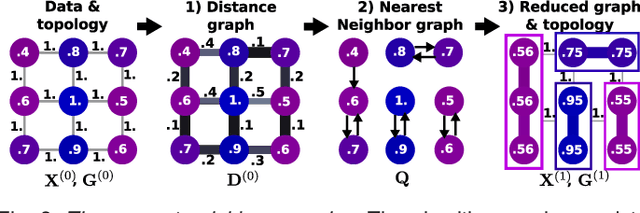
In this work, we revisit fast dimension reduction approaches, as with random projections and random sampling. Our goal is to summarize the data to decrease computational costs and memory footprint of subsequent analysis. Such dimension reduction can be very efficient when the signals of interest have a strong structure, such as with images. We focus on this setting and investigate feature clustering schemes for data reductions that capture this structure. An impediment to fast dimension reduction is that good clustering comes with large algorithmic costs. We address it by contributing a linear-time agglomerative clustering scheme, Recursive Nearest Agglomeration (ReNA). Unlike existing fast agglomerative schemes, it avoids the creation of giant clusters. We empirically validate that it approximates the data as well as traditional variance-minimizing clustering schemes that have a quadratic complexity. In addition, we analyze signal approximation with feature clustering and show that it can remove noise, improving subsequent analysis steps. As a consequence, data reduction by clustering features with ReNA yields very fast and accurate models, enabling to process large datasets on budget. Our theoretical analysis is backed by extensive experiments on publicly-available data that illustrate the computation efficiency and the denoising properties of the resulting dimension reduction scheme.

Assessing and tuning brain decoders: cross-validation, caveats, and guidelines

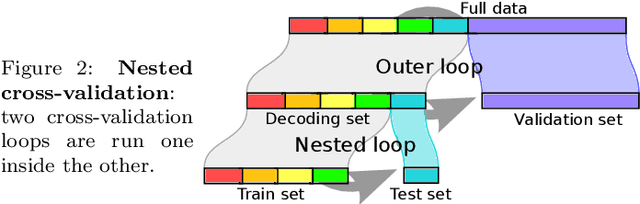
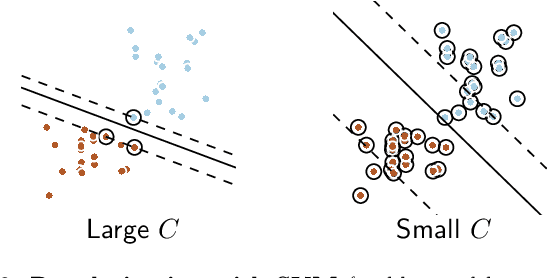
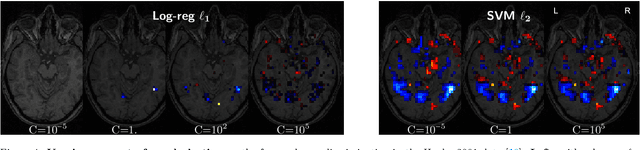
Decoding, ie prediction from brain images or signals, calls for empirical evaluation of its predictive power. Such evaluation is achieved via cross-validation, a method also used to tune decoders' hyper-parameters. This paper is a review on cross-validation procedures for decoding in neuroimaging. It includes a didactic overview of the relevant theoretical considerations. Practical aspects are highlighted with an extensive empirical study of the common decoders in within-and across-subject predictions, on multiple datasets --anatomical and functional MRI and MEG-- and simulations. Theory and experiments outline that the popular " leave-one-out " strategy leads to unstable and biased estimates, and a repeated random splits method should be preferred. Experiments outline the large error bars of cross-validation in neuroimaging settings: typical confidence intervals of 10%. Nested cross-validation can tune decoders' parameters while avoiding circularity bias. However we find that it can be more favorable to use sane defaults, in particular for non-sparse decoders.

Fast clustering for scalable statistical analysis on structured images

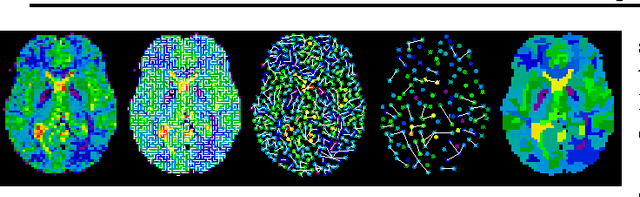
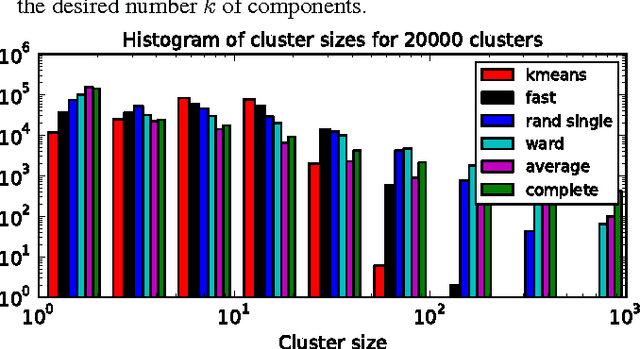
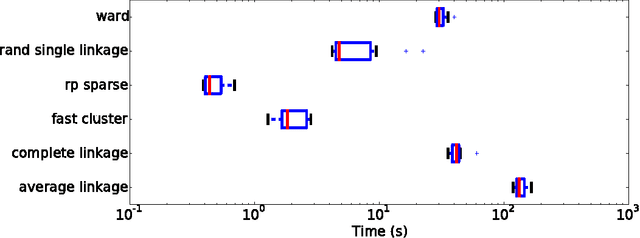
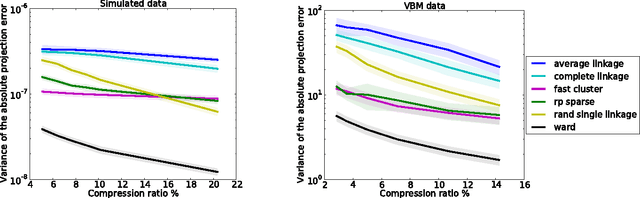
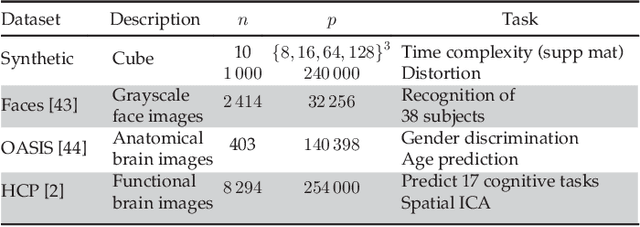
The use of brain images as markers for diseases or behavioral differences is challenged by the small effects size and the ensuing lack of power, an issue that has incited researchers to rely more systematically on large cohorts. Coupled with resolution increases, this leads to very large datasets. A striking example in the case of brain imaging is that of the Human Connectome Project: 20 Terabytes of data and growing. The resulting data deluge poses severe challenges regarding the tractability of some processing steps (discriminant analysis, multivariate models) due to the memory demands posed by these data. In this work, we revisit dimension reduction approaches, such as random projections, with the aim of replacing costly function evaluations by cheaper ones while decreasing the memory requirements. Specifically, we investigate the use of alternate schemes, based on fast clustering, that are well suited for signals exhibiting a strong spatial structure, such as anatomical and functional brain images. Our contribution is twofold: i) we propose a linear-time clustering scheme that bypasses the percolation issues inherent in these algorithms and thus provides compressions nearly as good as traditional quadratic-complexity variance-minimizing clustering schemes, ii) we show that cluster-based compression can have the virtuous effect of removing high-frequency noise, actually improving subsequent estimations steps. As a consequence, the proposed approach yields very accurate models on several large-scale problems yet with impressive gains in computational efficiency, making it possible to analyze large datasets.