Local Bures-Wasserstein Transport: A Practical and Fast Mapping Approximation
Paper and Code
Jun 19, 2019

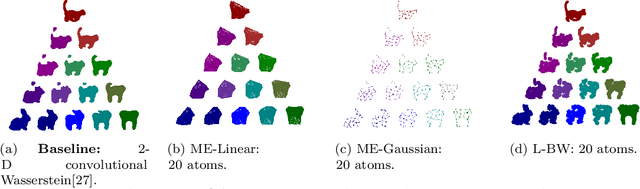
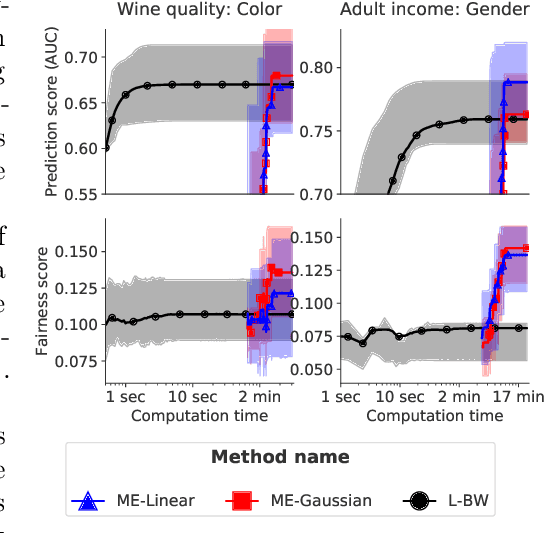
Optimal transport (OT)-based methods have a wide range of applications and have attracted a tremendous amount of attention in recent years. However, most of the computational approaches of OT do not learn the underlying transport map. Although some algorithms have been proposed to learn this map, they rely on kernel-based methods, which makes them prohibitively slow when the number of samples increases. Here, we propose a way to learn an approximate transport map and a parametric approximation of the Wasserstein barycenter. We build an approximated transport mapping by leveraging the closed-form of Gaussian (Bures-Wasserstein) transport; we compute local transport plans between matched pairs of the Gaussian components of each density. The learned map generalizes to out-of-sample examples. We provide experimental results on simulated and real data, comparing our proposed method with other mapping estimation algorithms. Preliminary experiments suggest that our proposed method is not only faster, with a factor 80 overall running time, but it also requires fewer components than state-of-the-art methods to recover the support of the barycenter. From a practical standpoint, it is straightforward to implement and can be used with a conventional machine learning pipeline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge