Learning to Re-rank with Constrained Meta-Optimal Transport
Paper and Code
Apr 29, 2023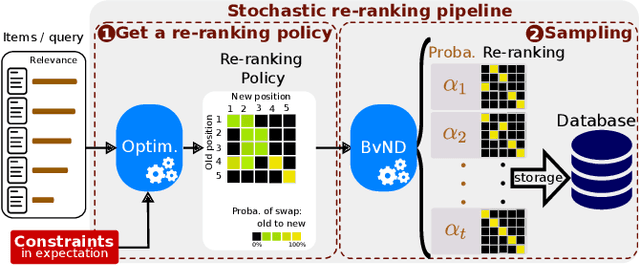
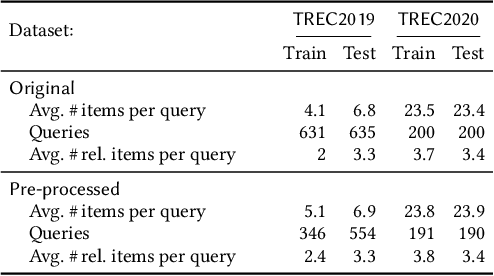
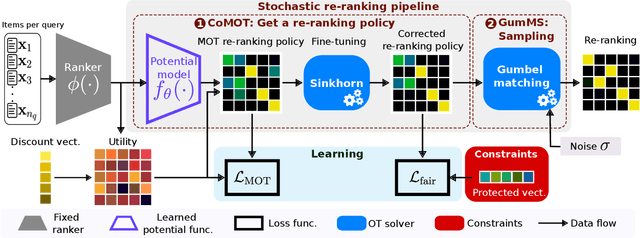
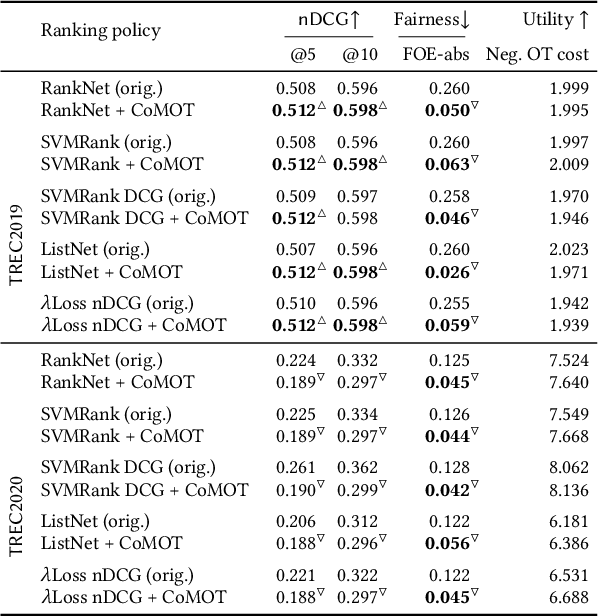
Many re-ranking strategies in search systems rely on stochastic ranking policies, encoded as Doubly-Stochastic (DS) matrices, that satisfy desired ranking constraints in expectation, e.g., Fairness of Exposure (FOE). These strategies are generally two-stage pipelines: \emph{i)} an offline re-ranking policy construction step and \emph{ii)} an online sampling of rankings step. Building a re-ranking policy requires repeatedly solving a constrained optimization problem, one for each issued query. Thus, it is necessary to recompute the optimization procedure for any new/unseen query. Regarding sampling, the Birkhoff-von-Neumann decomposition (BvND) is the favored approach to draw rankings from any DS-based policy. However, the BvND is too costly to compute online. Hence, the BvND as a sampling solution is memory-consuming as it can grow as $\gO(N\, n^2)$ for $N$ queries and $n$ documents. This paper offers a novel, fast, lightweight way to predict fair stochastic re-ranking policies: Constrained Meta-Optimal Transport (CoMOT). This method fits a neural network shared across queries like a learning-to-rank system. We also introduce Gumbel-Matching Sampling (GumMS), an online sampling approach from DS-based policies. Our proposed pipeline, CoMOT + GumMS, only needs to store the parameters of a single model, and it generalizes to unseen queries. We empirically evaluated our pipeline on the TREC 2019 and 2020 datasets under FOE constraints. Our experiments show that CoMOT rapidly predicts fair re-ranking policies on held-out data, with a speed-up proportional to the average number of documents per query. It also displays fairness and ranking performance similar to the original optimization-based policy. Furthermore, we empirically validate the effectiveness of GumMS to approximate DS-based policies in expectation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge