Data-Driven Inverse Reinforcement Learning for Expert-Learner Zero-Sum Games

In this paper, we formulate inverse reinforcement learning (IRL) as an expert-learner interaction whereby the optimal performance intent of an expert or target agent is unknown to a learner agent. The learner observes the states and controls of the expert and hence seeks to reconstruct the expert's cost function intent and thus mimics the expert's optimal response. Next, we add non-cooperative disturbances that seek to disrupt the learning and stability of the learner agent. This leads to the formulation of a new interaction we call zero-sum game IRL. We develop a framework to solve the zero-sum game IRL problem that is a modified extension of RL policy iteration (PI) to allow unknown expert performance intentions to be computed and non-cooperative disturbances to be rejected. The framework has two parts: a value function and control action update based on an extension of PI, and a cost function update based on standard inverse optimal control. Then, we eventually develop an off-policy IRL algorithm that does not require knowledge of the expert and learner agent dynamics and performs single-loop learning. Rigorous proofs and analyses are given. Finally, simulation experiments are presented to show the effectiveness of the new approach.

Learning nonlinear dynamics in synchronization of knowledge-based leader-following networks

Knowledge-based leader-following synchronization problem of heterogeneous nonlinear multi-agent systems is challenging since the leader's dynamic information is unknown to all follower nodes. This paper proposes a learning-based fully distributed observer for a class of nonlinear leader systems, which can simultaneously learn the leader's dynamics and states. The class of leader dynamics considered here does not require a bounded Jacobian matrix. Based on this learning-based distributed observer, we further synthesize an adaptive distributed control law for solving the leader-following synchronization problem of multiple Euler-Lagrange systems subject to an uncertain nonlinear leader system. The results are illustrated by a simulation example.

Neural Network iLQR: A New Reinforcement Learning Architecture

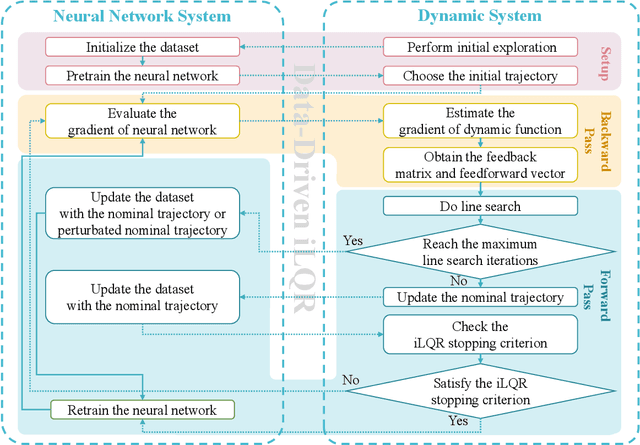
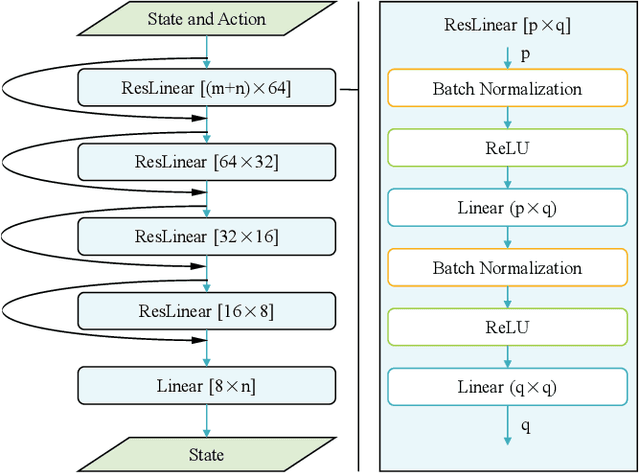
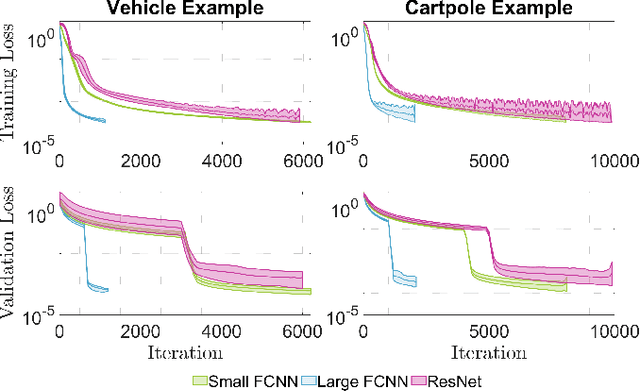
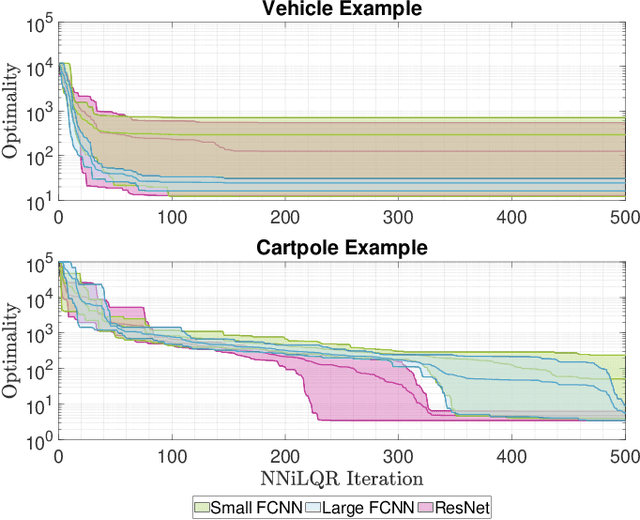
As a notable machine learning paradigm, the research efforts in the context of reinforcement learning have certainly progressed leaps and bounds. When compared with reinforcement learning methods with the given system model, the methodology of the reinforcement learning architecture based on the unknown model generally exhibits significantly broader universality and applicability. In this work, a new reinforcement learning architecture is developed and presented without the requirement of any prior knowledge of the system model, which is termed as an approach of a "neural network iterative linear quadratic regulator (NNiLQR)". Depending solely on measurement data, this method yields a completely new non-parametric routine for the establishment of the optimal policy (without the necessity of system modeling) through iterative refinements of the neural network system. Rather importantly, this approach significantly outperforms the classical iterative linear quadratic regulator (iLQR) method in terms of the given objective function because of the innovative utilization of further exploration in the methodology. As clearly indicated from the results attained in two illustrative examples, these significant merits of the NNiLQR method are demonstrated rather evidently.

Local Policy Optimization for Trajectory-Centric Reinforcement Learning

The goal of this paper is to present a method for simultaneous trajectory and local stabilizing policy optimization to generate local policies for trajectory-centric model-based reinforcement learning (MBRL). This is motivated by the fact that global policy optimization for non-linear systems could be a very challenging problem both algorithmically and numerically. However, a lot of robotic manipulation tasks are trajectory-centric, and thus do not require a global model or policy. Due to inaccuracies in the learned model estimates, an open-loop trajectory optimization process mostly results in very poor performance when used on the real system. Motivated by these problems, we try to formulate the problem of trajectory optimization and local policy synthesis as a single optimization problem. It is then solved simultaneously as an instance of nonlinear programming. We provide some results for analysis as well as achieved performance of the proposed technique under some simplifying assumptions.