A Symmetry-Aware Exploration of Bayesian Neural Network Posteriors

The distribution of the weights of modern deep neural networks (DNNs) - crucial for uncertainty quantification and robustness - is an eminently complex object due to its extremely high dimensionality. This paper proposes one of the first large-scale explorations of the posterior distribution of deep Bayesian Neural Networks (BNNs), expanding its study to real-world vision tasks and architectures. Specifically, we investigate the optimal approach for approximating the posterior, analyze the connection between posterior quality and uncertainty quantification, delve into the impact of modes on the posterior, and explore methods for visualizing the posterior. Moreover, we uncover weight-space symmetries as a critical aspect for understanding the posterior. To this extent, we develop an in-depth assessment of the impact of both permutation and scaling symmetries that tend to obfuscate the Bayesian posterior. While the first type of transformation is known for duplicating modes, we explore the relationship between the latter and L2 regularization, challenging previous misconceptions. Finally, to help the community improve our understanding of the Bayesian posterior, we will shortly release the first large-scale checkpoint dataset, including thousands of real-world models and our codes.

Discretization-Induced Dirichlet Posterior for Robust Uncertainty Quantification on Regression

Uncertainty quantification is critical for deploying deep neural networks (DNNs) in real-world applications. An Auxiliary Uncertainty Estimator (AuxUE) is one of the most effective means to estimate the uncertainty of the main task prediction without modifying the main task model. To be considered robust, an AuxUE must be capable of maintaining its performance and triggering higher uncertainties while encountering Out-of-Distribution (OOD) inputs, i.e., to provide robust aleatoric and epistemic uncertainty. However, for vision regression tasks, current AuxUE designs are mainly adopted for aleatoric uncertainty estimates, and AuxUE robustness has not been explored. In this work, we propose a generalized AuxUE scheme for more robust uncertainty quantification on regression tasks. Concretely, to achieve a more robust aleatoric uncertainty estimation, different distribution assumptions are considered for heteroscedastic noise, and Laplace distribution is finally chosen to approximate the prediction error. For epistemic uncertainty, we propose a novel solution named Discretization-Induced Dirichlet pOsterior (DIDO), which models the Dirichlet posterior on the discretized prediction error. Extensive experiments on age estimation, monocular depth estimation, and super-resolution tasks show that our proposed method can provide robust uncertainty estimates in the face of noisy inputs and that it can be scalable to both image-level and pixel-wise tasks.

Latent Discriminant deterministic Uncertainty

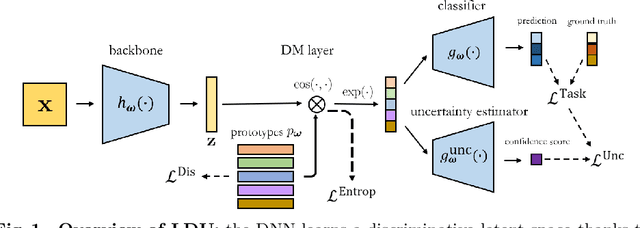
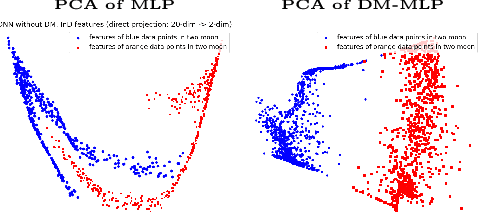
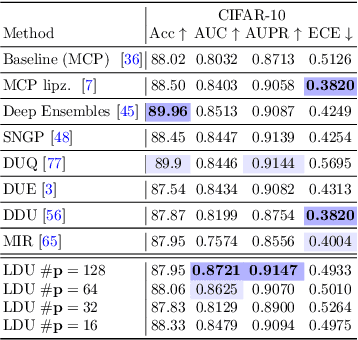
Predictive uncertainty estimation is essential for deploying Deep Neural Networks in real-world autonomous systems. However, most successful approaches are computationally intensive. In this work, we attempt to address these challenges in the context of autonomous driving perception tasks. Recently proposed Deterministic Uncertainty Methods (DUM) can only partially meet such requirements as their scalability to complex computer vision tasks is not obvious. In this work we advance a scalable and effective DUM for high-resolution semantic segmentation, that relaxes the Lipschitz constraint typically hindering practicality of such architectures. We learn a discriminant latent space by leveraging a distinction maximization layer over an arbitrarily-sized set of trainable prototypes. Our approach achieves competitive results over Deep Ensembles, the state-of-the-art for uncertainty prediction, on image classification, segmentation and monocular depth estimation tasks. Our code is available at https://github.com/ENSTA-U2IS/LDU

MUAD: Multiple Uncertainties for Autonomous Driving benchmark for multiple uncertainty types and tasks

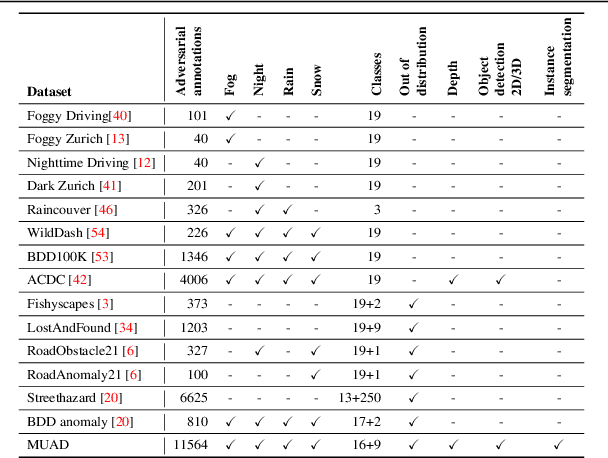
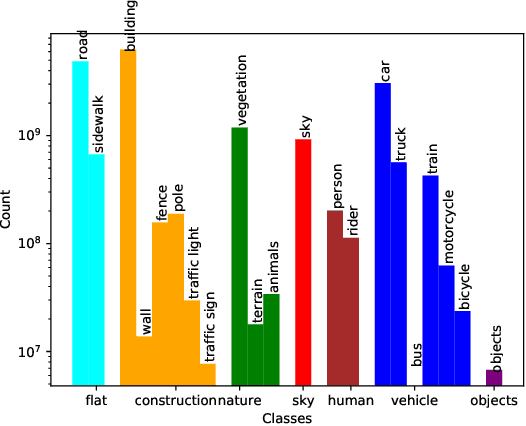
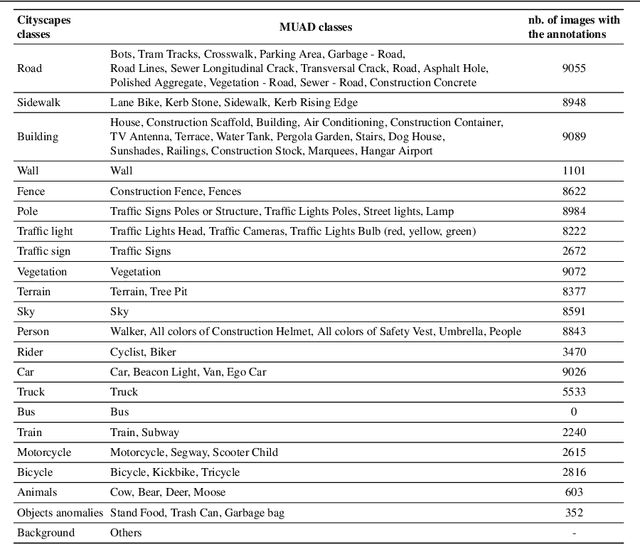
Predictive uncertainty estimation is essential for deploying Deep Neural Networks in real-world autonomous systems. However, disentangling the different types and sources of uncertainty is non trivial in most datasets, especially since there is no ground truth for uncertainty. In addition, different degrees of weather conditions can disrupt neural networks, resulting in inconsistent training data quality. Thus, we introduce the MUAD dataset (Multiple Uncertainties for Autonomous Driving), consisting of 8,500 realistic synthetic images with diverse adverse weather conditions (night, fog, rain, snow), out-of-distribution objects and annotations for semantic segmentation, depth estimation, object and instance detection. MUAD allows to better assess the impact of different sources of uncertainty on model performance. We propose a study that shows the importance of having reliable Deep Neural Networks (DNNs) in multiple experiments, and will release our dataset to allow researchers to benchmark their algorithm methodically in ad-verse conditions. More information and the download link for MUAD are available at https://muad-dataset.github.io/ .

On Monocular Depth Estimation and Uncertainty Quantification using Classification Approaches for Regression

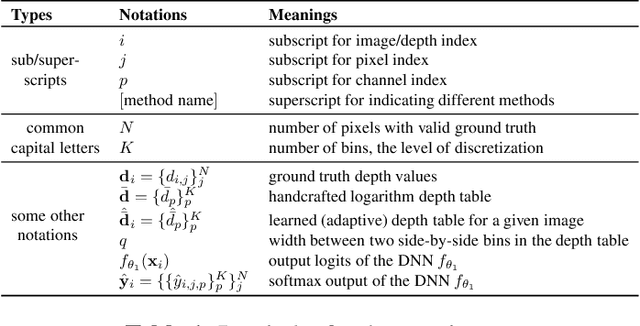
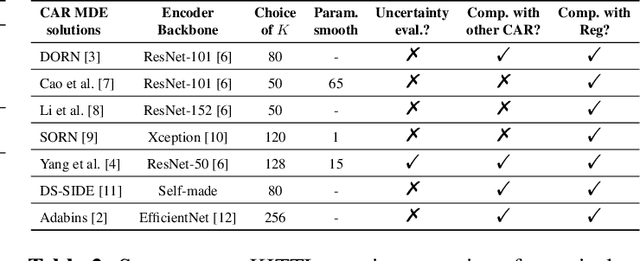
Monocular depth is important in many tasks, such as 3D reconstruction and autonomous driving. Deep learning based models achieve state-of-the-art performance in this field. A set of novel approaches for estimating monocular depth consists of transforming the regression task into a classification one. However, there is a lack of detailed descriptions and comparisons for Classification Approaches for Regression (CAR) in the community and no in-depth exploration of their potential for uncertainty estimation. To this end, this paper will introduce a taxonomy and summary of CAR approaches, a new uncertainty estimation solution for CAR, and a set of experiments on depth accuracy and uncertainty quantification for CAR-based models on KITTI dataset. The experiments reflect the differences in the portability of various CAR methods on two backbones. Meanwhile, the newly proposed method for uncertainty estimation can outperform the ensembling method with only one forward propagation.

SLURP: Side Learning Uncertainty for Regression Problems

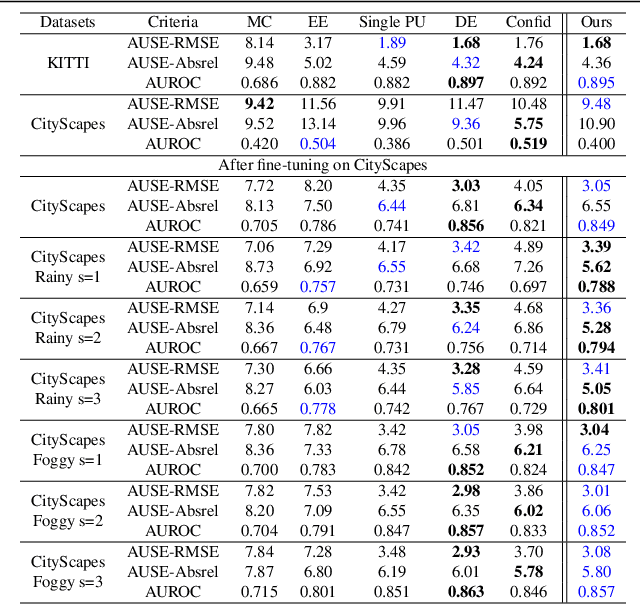
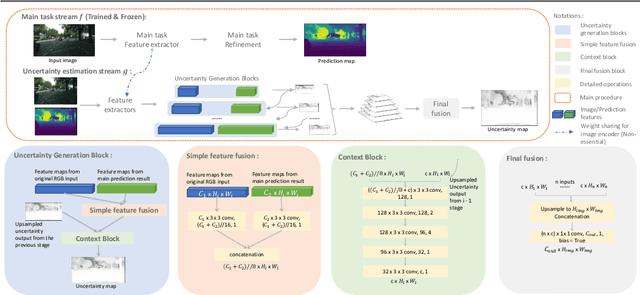
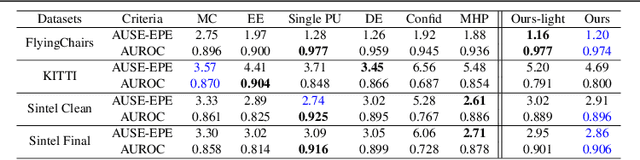
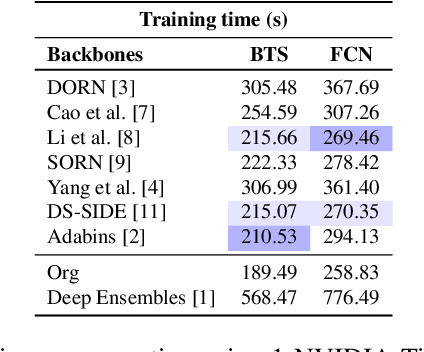
It has become critical for deep learning algorithms to quantify their output uncertainties to satisfy reliability constraints and provide accurate results. Uncertainty estimation for regression has received less attention than classification due to the more straightforward standardized output of the latter class of tasks and their high importance. However, regression problems are encountered in a wide range of applications in computer vision. We propose SLURP, a generic approach for regression uncertainty estimation via a side learner that exploits the output and the intermediate representations generated by the main task model. We test SLURP on two critical regression tasks in computer vision: monocular depth and optical flow estimation. In addition, we conduct exhaustive benchmarks comprising transfer to different datasets and the addition of aleatoric noise. The results show that our proposal is generic and readily applicable to various regression problems and has a low computational cost with respect to existing solutions.

Learning a Discriminant Latent Space with Neural Discriminant Analysis

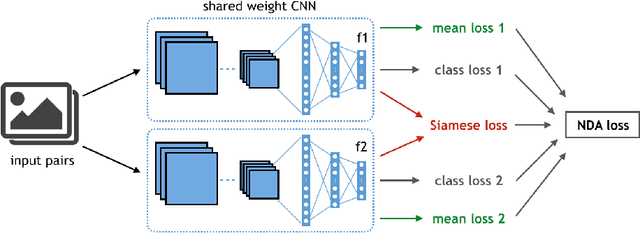
Discriminative features play an important role in image and object classification and also in other fields of research such as semi-supervised learning, fine-grained classification, out of distribution detection. Inspired by Linear Discriminant Analysis (LDA), we propose an optimization called Neural Discriminant Analysis (NDA) for Deep Convolutional Neural Networks (DCNNs). NDA transforms deep features to become more discriminative and, therefore, improves the performances in various tasks. Our proposed optimization has two primary goals for inter- and intra-class variances. The first one is to minimize variances within each individual class. The second goal is to maximize pairwise distances between features coming from different classes. We evaluate our NDA optimization in different research fields: general supervised classification, fine-grained classification, semi-supervised learning, and out of distribution detection. We achieve performance improvements in all the fields compared to baseline methods that do not use NDA. Besides, using NDA, we also surpass the state of the art on the four tasks on various testing datasets.

Encoding the latent posterior of Bayesian Neural Networks for uncertainty quantification

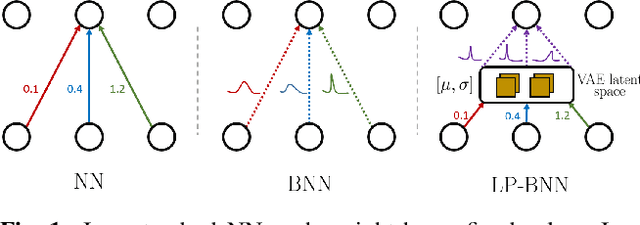
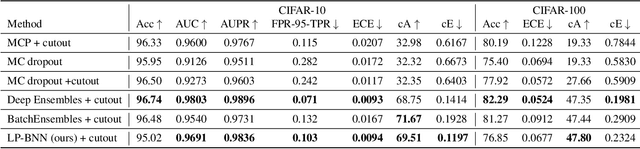
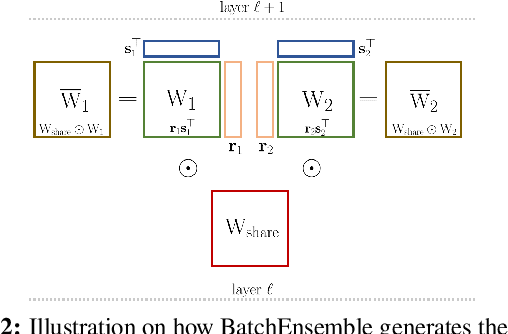
Bayesian neural networks (BNNs) have been long considered an ideal, yet unscalable solution for improving the robustness and the predictive uncertainty of deep neural networks. While they could capture more accurately the posterior distribution of the network parameters, most BNN approaches are either limited to small networks or rely on constraining assumptions such as parameter independence. These drawbacks have enabled prominence of simple, but computationally heavy approaches such as Deep Ensembles, whose training and testing costs increase linearly with the number of networks. In this work we aim for efficient deep BNNs amenable to complex computer vision architectures, e.g. ResNet50 DeepLabV3+, and tasks, e.g. semantic segmentation, with fewer assumptions on the parameters. We achieve this by leveraging variational autoencoders (VAEs) to learn the interaction and the latent distribution of the parameters at each network layer. Our approach, Latent-Posterior BNN (LP-BNN), is compatible with the recent BatchEnsemble method, leading to highly efficient ({in terms of computation and} memory during both training and testing) ensembles. LP-BNN s attain competitive results across multiple metrics in several challenging benchmarks for image classification, semantic segmentation and out-of-distribution detection.

One Versus all for deep Neural Network Incertitude quantification

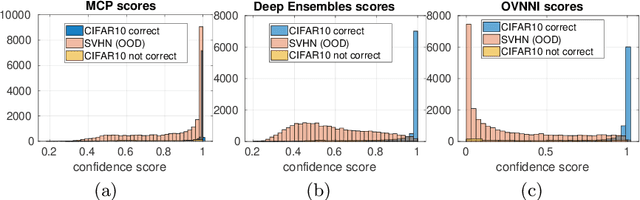
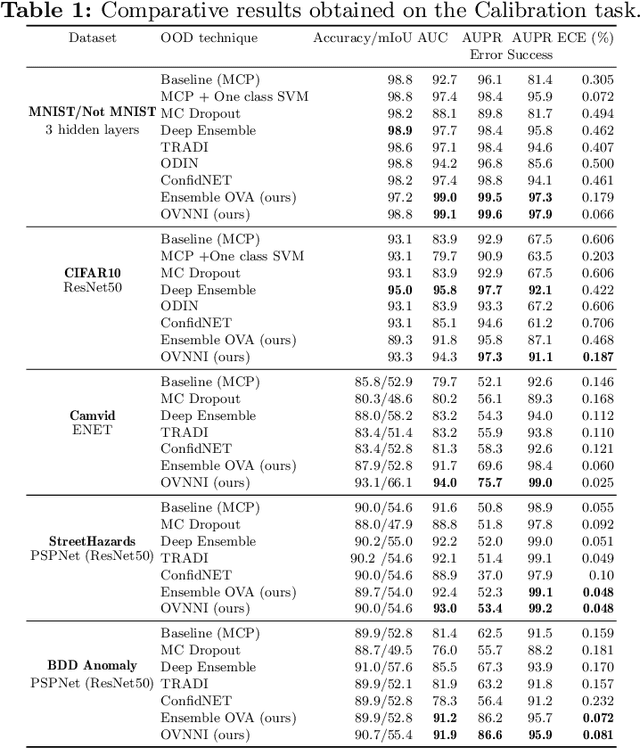
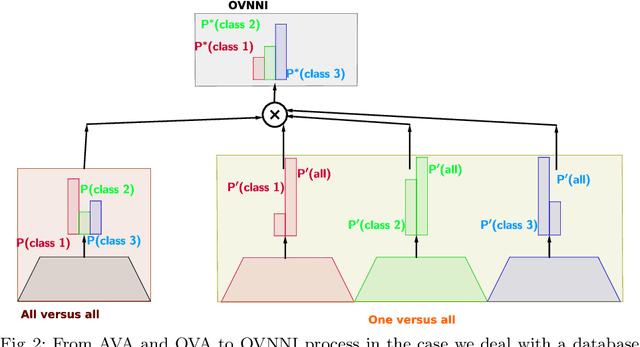
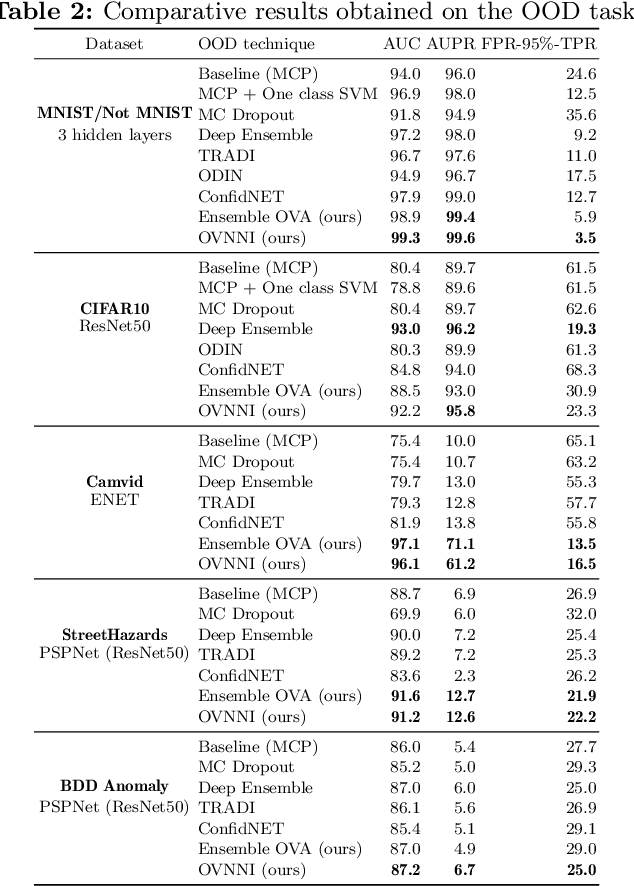
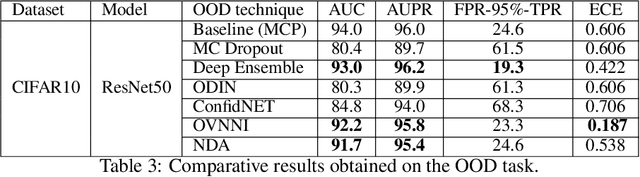
Deep neural networks (DNNs) are powerful learning models yet their results are not always reliable. This is due to the fact that modern DNNs are usually uncalibrated and we cannot characterize their epistemic uncertainty. In this work, we propose a new technique to quantify the epistemic uncertainty of data easily. This method consists in mixing the predictions of an ensemble of DNNs trained to classify One class vs All the other classes (OVA) with predictions from a standard DNN trained to perform All vs All (AVA) classification. On the one hand, the adjustment provided by the AVA DNN to the score of the base classifiers allows for a more fine-grained inter-class separation. On the other hand, the two types of classifiers enforce mutually their detection of out-of-distribution (OOD) samples, circumventing entirely the requirement of using such samples during training. Our method achieves state of the art performance in quantifying OOD data across multiple datasets and architectures while requiring little hyper-parameter tuning.

TRADI: Tracking deep neural network weight distributions

During training, the weights of a Deep Neural Network (DNN) are optimized from a random initialization towards a nearly optimum value minimizing a loss function. Only this final state of the weights is typically kept for testing, while the wealth of information on the geometry of the weight space, accumulated over the descent towards the minimum is discarded. In this work we propose to make use of this knowledge and leverage it for computing the distributions of the weights of the DNN. This can be further used for estimating the epistemic uncertainty of the DNN by sampling an ensemble of networks from these distributions. To this end we introduce a method for tracking the trajectory of the weights during optimization, that does not require any changes in the architecture nor on the training procedure. We evaluate our method on standard classification and regression benchmarks, and on out-of-distribution detection for classification and semantic segmentation. We achieve competitive results, while preserving computational efficiency in comparison to other popular approaches.