Efficient Video Face Enhancement with Enhanced Spatial-Temporal Consistency

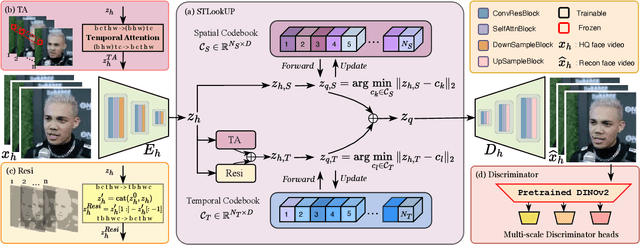
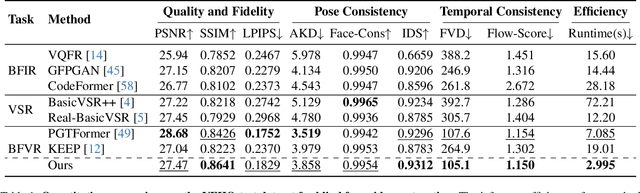
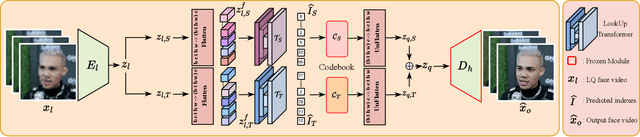
As a very common type of video, face videos often appear in movies, talk shows, live broadcasts, and other scenes. Real-world online videos are often plagued by degradations such as blurring and quantization noise, due to the high compression ratio caused by high communication costs and limited transmission bandwidth. These degradations have a particularly serious impact on face videos because the human visual system is highly sensitive to facial details. Despite the significant advancement in video face enhancement, current methods still suffer from $i)$ long processing time and $ii)$ inconsistent spatial-temporal visual effects (e.g., flickering). This study proposes a novel and efficient blind video face enhancement method to overcome the above two challenges, restoring high-quality videos from their compressed low-quality versions with an effective de-flickering mechanism. In particular, the proposed method develops upon a 3D-VQGAN backbone associated with spatial-temporal codebooks recording high-quality portrait features and residual-based temporal information. We develop a two-stage learning framework for the model. In Stage \Rmnum{1}, we learn the model with a regularizer mitigating the codebook collapse problem. In Stage \Rmnum{2}, we learn two transformers to lookup code from the codebooks and further update the encoder of low-quality videos. Experiments conducted on the VFHQ-Test dataset demonstrate that our method surpasses the current state-of-the-art blind face video restoration and de-flickering methods on both efficiency and effectiveness. Code is available at \url{https://github.com/Dixin-Lab/BFVR-STC}.

Generalizable Face Landmarking Guided by Conditional Face Warping

As a significant step for human face modeling, editing, and generation, face landmarking aims at extracting facial keypoints from images. A generalizable face landmarker is required in practice because real-world facial images, e.g., the avatars in animations and games, are often stylized in various ways. However, achieving generalizable face landmarking is challenging due to the diversity of facial styles and the scarcity of labeled stylized faces. In this study, we propose a simple but effective paradigm to learn a generalizable face landmarker based on labeled real human faces and unlabeled stylized faces. Our method learns the face landmarker as the key module of a conditional face warper. Given a pair of real and stylized facial images, the conditional face warper predicts a warping field from the real face to the stylized one, in which the face landmarker predicts the ending points of the warping field and provides us with high-quality pseudo landmarks for the corresponding stylized facial images. Applying an alternating optimization strategy, we learn the face landmarker to minimize $i)$ the discrepancy between the stylized faces and the warped real ones and $ii)$ the prediction errors of both real and pseudo landmarks. Experiments on various datasets show that our method outperforms existing state-of-the-art domain adaptation methods in face landmarking tasks, leading to a face landmarker with better generalizability. Code is available at https://plustwo0.github.io/project-face-landmarker}{https://plustwo0.github.io/project-face-landmarker.

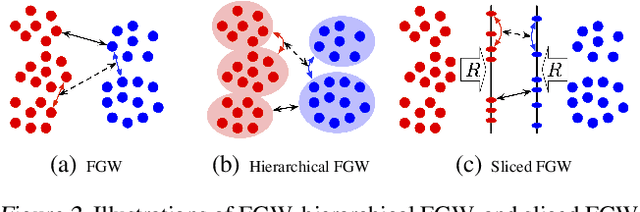
DHOT-GM: Robust Graph Matching Using A Differentiable Hierarchical Optimal Transport Framework

Graph matching is one of the most significant graph analytic tasks in practice, which aims to find the node correspondence across different graphs. Most existing approaches rely on adjacency matrices or node embeddings when matching graphs, whose performances are often sub-optimal because of not fully leveraging the multi-modal information hidden in graphs, such as node attributes, subgraph structures, etc. In this study, we propose a novel and effective graph matching method based on a differentiable hierarchical optimal transport (HOT) framework, called DHOT-GM. Essentially, our method represents each graph as a set of relational matrices corresponding to the information of different modalities. Given two graphs, we enumerate all relational matrix pairs and obtain their matching results, and accordingly, infer the node correspondence by the weighted averaging of the matching results. This method can be implemented as computing the HOT distance between the two graphs -- each matching result is an optimal transport plan associated with the Gromov-Wasserstein (GW) distance between two relational matrices, and the weights of all matching results are the elements of an upper-level optimal transport plan defined on the matrix sets. We propose a bi-level optimization algorithm to compute the HOT distance in a differentiable way, making the significance of the relational matrices adjustable. Experiments on various graph matching tasks demonstrate the superiority and robustness of our method compared to state-of-the-art approaches.

Learning Graphon Autoencoders for Generative Graph Modeling

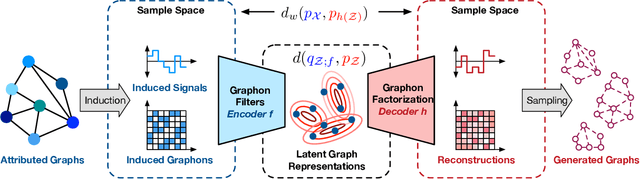
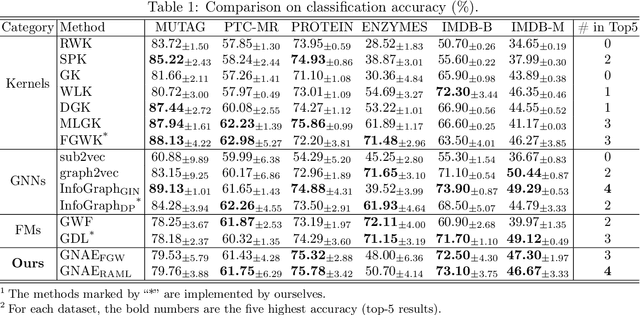
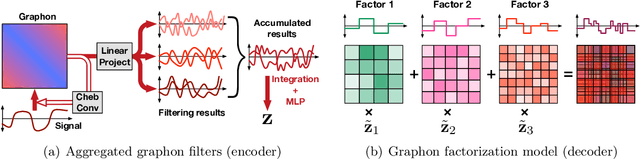
Graphon is a nonparametric model that generates graphs with arbitrary sizes and can be induced from graphs easily. Based on this model, we propose a novel algorithmic framework called \textit{graphon autoencoder} to build an interpretable and scalable graph generative model. This framework treats observed graphs as induced graphons in functional space and derives their latent representations by an encoder that aggregates Chebshev graphon filters. A linear graphon factorization model works as a decoder, leveraging the latent representations to reconstruct the induced graphons (and the corresponding observed graphs). We develop an efficient learning algorithm to learn the encoder and the decoder, minimizing the Wasserstein distance between the model and data distributions. This algorithm takes the KL divergence of the graph distributions conditioned on different graphons as the underlying distance and leads to a reward-augmented maximum likelihood estimation. The graphon autoencoder provides a new paradigm to represent and generate graphs, which has good generalizability and transferability.

Hawkes Processes on Graphons

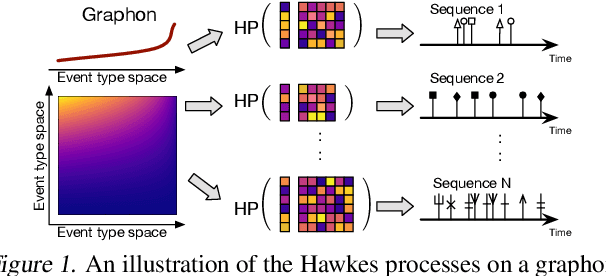
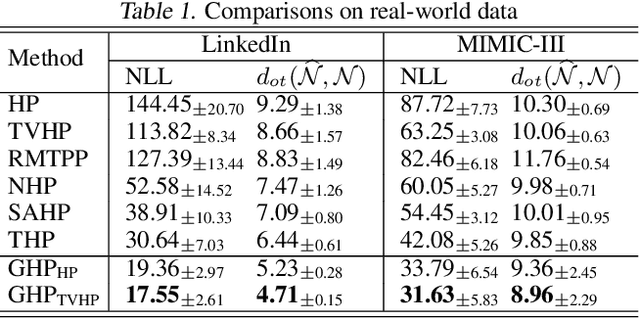
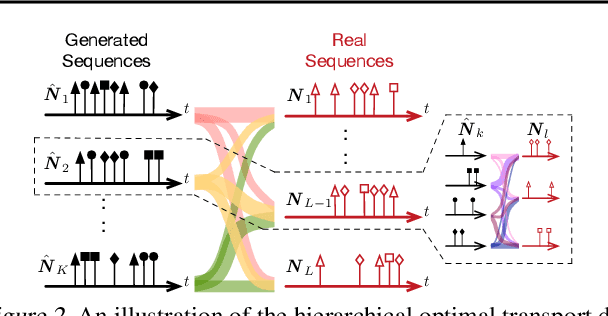
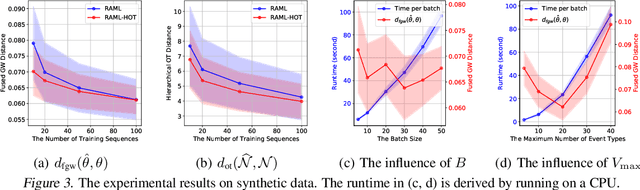
We propose a novel framework for modeling multiple multivariate point processes, each with heterogeneous event types that share an underlying space and obey the same generative mechanism. Focusing on Hawkes processes and their variants that are associated with Granger causality graphs, our model leverages an uncountable event type space and samples the graphs with different sizes from a nonparametric model called {\it graphon}. Given those graphs, we can generate the corresponding Hawkes processes and simulate event sequences. Learning this graphon-based Hawkes process model helps to 1) infer the underlying relations shared by different Hawkes processes; and 2) simulate event sequences with different event types but similar dynamics. We learn the proposed model by minimizing the hierarchical optimal transport distance between the generated event sequences and the observed ones, leading to a novel reward-augmented maximum likelihood estimation method. We analyze the properties of our model in-depth and demonstrate its rationality and effectiveness in both theory and experiments.

Learning Graphons via Structured Gromov-Wasserstein Barycenters

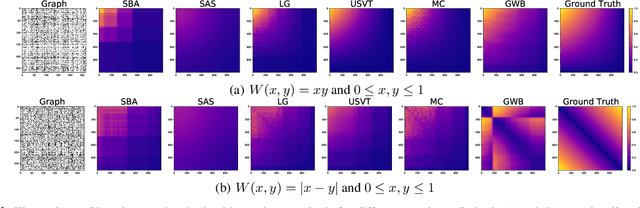
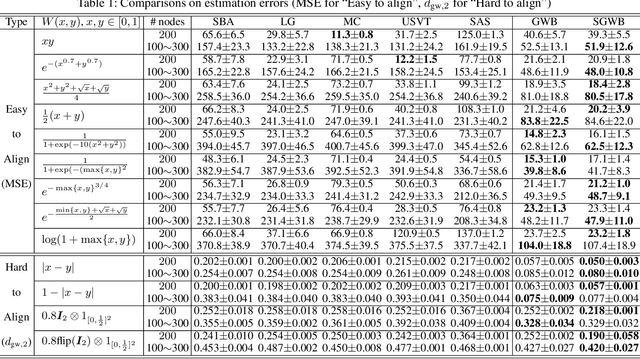
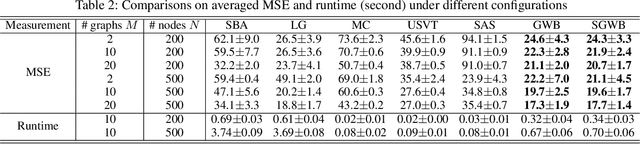
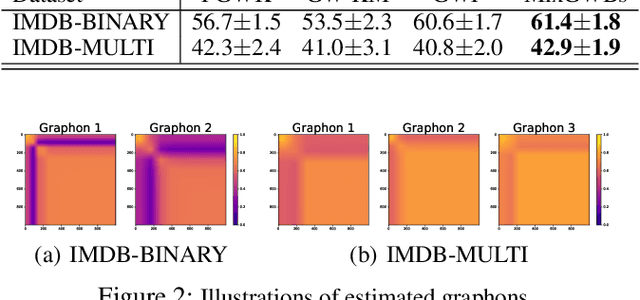
We propose a novel and principled method to learn a nonparametric graph model called graphon, which is defined in an infinite-dimensional space and represents arbitrary-size graphs. Based on the weak regularity lemma from the theory of graphons, we leverage a step function to approximate a graphon. We show that the cut distance of graphons can be relaxed to the Gromov-Wasserstein distance of their step functions. Accordingly, given a set of graphs generated by an underlying graphon, we learn the corresponding step function as the Gromov-Wasserstein barycenter of the given graphs. Furthermore, we develop several enhancements and extensions of the basic algorithm, $e.g.$, the smoothed Gromov-Wasserstein barycenter for guaranteeing the continuity of the learned graphons and the mixed Gromov-Wasserstein barycenters for learning multiple structured graphons. The proposed approach overcomes drawbacks of prior state-of-the-art methods, and outperforms them on both synthetic and real-world data. The code is available at https://github.com/HongtengXu/SGWB-Graphon.

Hierarchical Optimal Transport for Robust Multi-View Learning

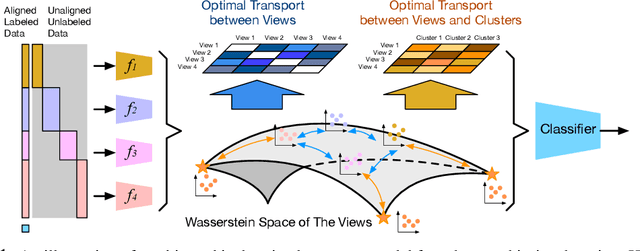
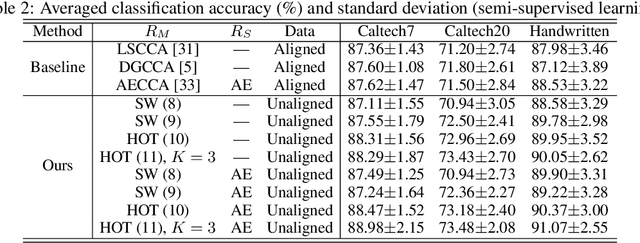
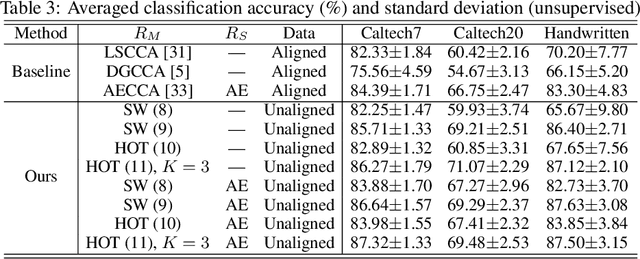
Traditional multi-view learning methods often rely on two assumptions: ($i$) the samples in different views are well-aligned, and ($ii$) their representations in latent space obey the same distribution. Unfortunately, these two assumptions may be questionable in practice, which limits the application of multi-view learning. In this work, we propose a hierarchical optimal transport (HOT) method to mitigate the dependency on these two assumptions. Given unaligned multi-view data, the HOT method penalizes the sliced Wasserstein distance between the distributions of different views. These sliced Wasserstein distances are used as the ground distance to calculate the entropic optimal transport across different views, which explicitly indicates the clustering structure of the views. The HOT method is applicable to both unsupervised and semi-supervised learning, and experimental results show that it performs robustly on both synthetic and real-world tasks.

Learning Autoencoders with Relational Regularization

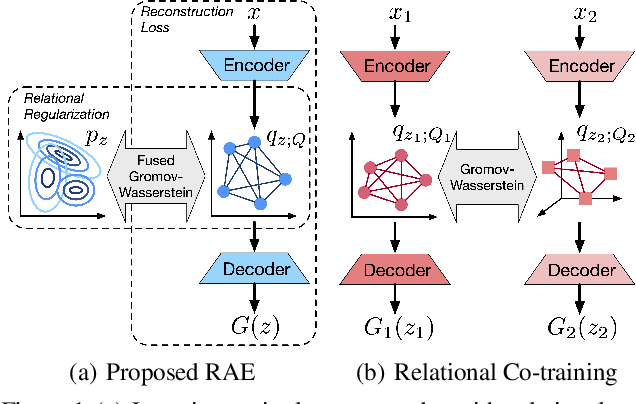
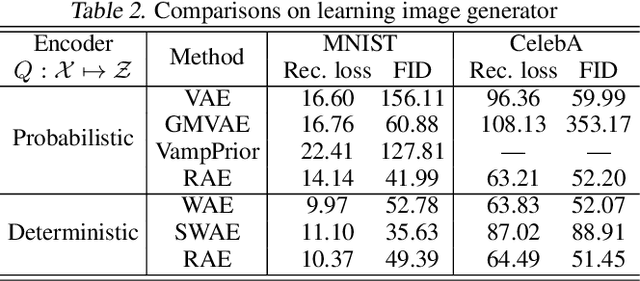
A new algorithmic framework is proposed for learning autoencoders of data distributions. We minimize the discrepancy between the model and target distributions, with a \emph{relational regularization} on the learnable latent prior. This regularization penalizes the fused Gromov-Wasserstein (FGW) distance between the latent prior and its corresponding posterior, allowing one to flexibly learn a structured prior distribution associated with the generative model. Moreover, it helps co-training of multiple autoencoders even if they have heterogeneous architectures and incomparable latent spaces. We implement the framework with two scalable algorithms, making it applicable for both probabilistic and deterministic autoencoders. Our relational regularized autoencoder (RAE) outperforms existing methods, $e.g.$, the variational autoencoder, Wasserstein autoencoder, and their variants, on generating images. Additionally, our relational co-training strategy for autoencoders achieves encouraging results in both synthesis and real-world multi-view learning tasks.

Fused Gromov-Wasserstein Alignment for Hawkes Processes

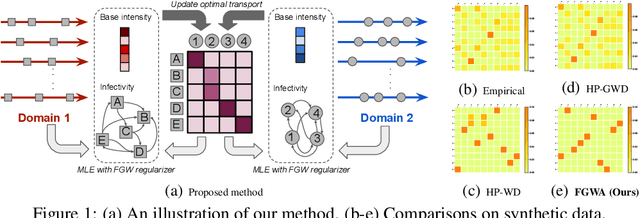
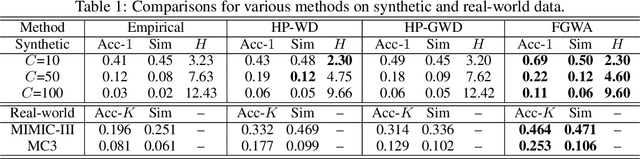
We propose a novel fused Gromov-Wasserstein alignment method to jointly learn the Hawkes processes in different event spaces, and align their event types. Given two Hawkes processes, we use fused Gromov-Wasserstein discrepancy to measure their dissimilarity, which considers both the Wasserstein discrepancy based on their base intensities and the Gromov-Wasserstein discrepancy based on their infectivity matrices. Accordingly, the learned optimal transport reflects the correspondence between the event types of these two Hawkes processes. The Hawkes processes and their optimal transport are learned jointly via maximum likelihood estimation, with a fused Gromov-Wasserstein regularizer. Experimental results show that the proposed method works well on synthetic and real-world data.

Adversarial Self-Paced Learning for Mixture Models of Hawkes Processes

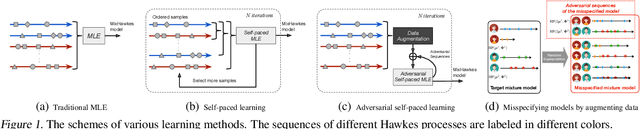
We propose a novel adversarial learning strategy for mixture models of Hawkes processes, leveraging data augmentation techniques of Hawkes process in the framework of self-paced learning. Instead of learning a mixture model directly from a set of event sequences drawn from different Hawkes processes, the proposed method learns the target model iteratively, which generates "easy" sequences and uses them in an adversarial and self-paced manner. In each iteration, we first generate a set of augmented sequences from original observed sequences. Based on the fact that an easy sample of the target model can be an adversarial sample of a misspecified model, we apply a maximum likelihood estimation with an adversarial self-paced mechanism. In this manner the target model is updated, and the augmented sequences that obey it are employed for the next learning iteration. Experimental results show that the proposed method outperforms traditional methods consistently.