Learning Graphon Autoencoders for Generative Graph Modeling
Paper and Code
May 29, 2021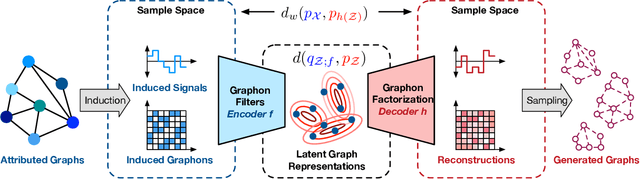
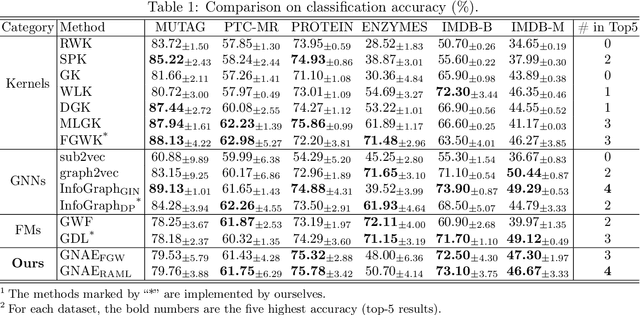
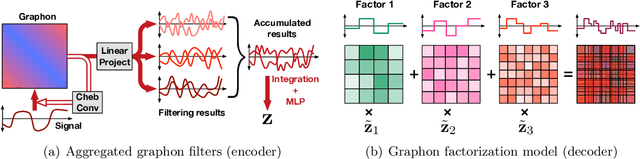

Graphon is a nonparametric model that generates graphs with arbitrary sizes and can be induced from graphs easily. Based on this model, we propose a novel algorithmic framework called \textit{graphon autoencoder} to build an interpretable and scalable graph generative model. This framework treats observed graphs as induced graphons in functional space and derives their latent representations by an encoder that aggregates Chebshev graphon filters. A linear graphon factorization model works as a decoder, leveraging the latent representations to reconstruct the induced graphons (and the corresponding observed graphs). We develop an efficient learning algorithm to learn the encoder and the decoder, minimizing the Wasserstein distance between the model and data distributions. This algorithm takes the KL divergence of the graph distributions conditioned on different graphons as the underlying distance and leads to a reward-augmented maximum likelihood estimation. The graphon autoencoder provides a new paradigm to represent and generate graphs, which has good generalizability and transferability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge