Fused Gromov-Wasserstein Alignment for Hawkes Processes
Paper and Code
Oct 04, 2019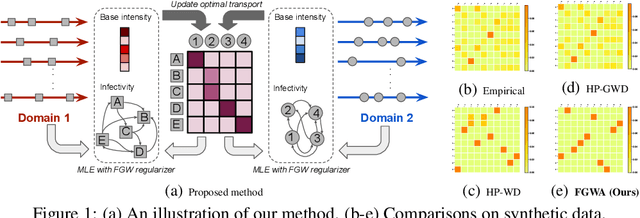
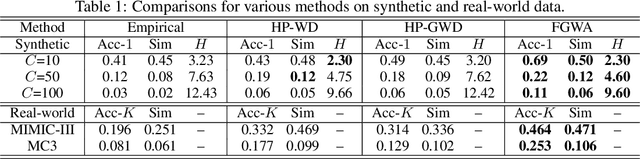
We propose a novel fused Gromov-Wasserstein alignment method to jointly learn the Hawkes processes in different event spaces, and align their event types. Given two Hawkes processes, we use fused Gromov-Wasserstein discrepancy to measure their dissimilarity, which considers both the Wasserstein discrepancy based on their base intensities and the Gromov-Wasserstein discrepancy based on their infectivity matrices. Accordingly, the learned optimal transport reflects the correspondence between the event types of these two Hawkes processes. The Hawkes processes and their optimal transport are learned jointly via maximum likelihood estimation, with a fused Gromov-Wasserstein regularizer. Experimental results show that the proposed method works well on synthetic and real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge