Learning Autoencoders with Relational Regularization

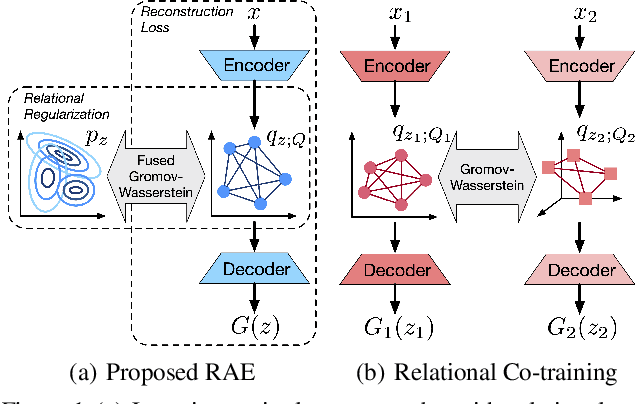
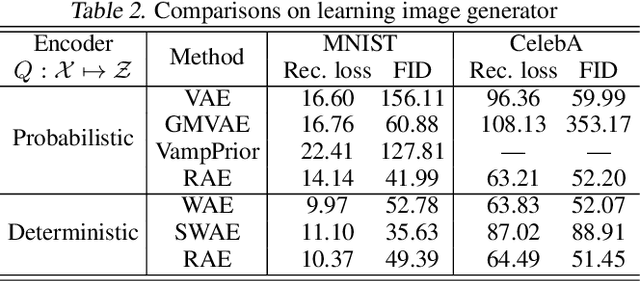
A new algorithmic framework is proposed for learning autoencoders of data distributions. We minimize the discrepancy between the model and target distributions, with a \emph{relational regularization} on the learnable latent prior. This regularization penalizes the fused Gromov-Wasserstein (FGW) distance between the latent prior and its corresponding posterior, allowing one to flexibly learn a structured prior distribution associated with the generative model. Moreover, it helps co-training of multiple autoencoders even if they have heterogeneous architectures and incomparable latent spaces. We implement the framework with two scalable algorithms, making it applicable for both probabilistic and deterministic autoencoders. Our relational regularized autoencoder (RAE) outperforms existing methods, $e.g.$, the variational autoencoder, Wasserstein autoencoder, and their variants, on generating images. Additionally, our relational co-training strategy for autoencoders achieves encouraging results in both synthesis and real-world multi-view learning tasks.