Wasserstein Flow Matching: Generative modeling over families of distributions

Generative modeling typically concerns the transport of a single source distribution to a single target distribution by learning (i.e., regressing onto) simple probability flows. However, in modern data-driven fields such as computer graphics and single-cell genomics, samples (say, point-clouds) from datasets can themselves be viewed as distributions (as, say, discrete measures). In these settings, the standard generative modeling paradigm of flow matching would ignore the relevant geometry of the samples. To remedy this, we propose \emph{Wasserstein flow matching} (WFM), which appropriately lifts flow matching onto families of distributions by appealing to the Riemannian nature of the Wasserstein geometry. Our algorithm leverages theoretical and computational advances in (entropic) optimal transport, as well as the attention mechanism in our neural network architecture. We present two novel algorithmic contributions. First, we demonstrate how to perform generative modeling over Gaussian distributions, where we generate representations of granular cell states from single-cell genomics data. Secondly, we show that WFM can learn flows between high-dimensional and variable sized point-clouds and synthesize cellular microenvironments from spatial transcriptomics datasets. Code is available at [WassersteinFlowMatching](https://github.com/DoronHav/WassersteinFlowMatching).

Wasserstein Wormhole: Scalable Optimal Transport Distance with Transformers

Optimal transport (OT) and the related Wasserstein metric (W) are powerful and ubiquitous tools for comparing distributions. However, computing pairwise Wasserstein distances rapidly becomes intractable as cohort size grows. An attractive alternative would be to find an embedding space in which pairwise Euclidean distances map to OT distances, akin to standard multidimensional scaling (MDS). We present Wasserstein Wormhole, a transformer-based autoencoder that embeds empirical distributions into a latent space wherein Euclidean distances approximate OT distances. Extending MDS theory, we show that our objective function implies a bound on the error incurred when embedding non-Euclidean distances. Empirically, distances between Wormhole embeddings closely match Wasserstein distances, enabling linear time computation of OT distances. Along with an encoder that maps distributions to embeddings, Wasserstein Wormhole includes a decoder that maps embeddings back to distributions, allowing for operations in the embedding space to generalize to OT spaces, such as Wasserstein barycenter estimation and OT interpolation. By lending scalability and interpretability to OT approaches, Wasserstein Wormhole unlocks new avenues for data analysis in the fields of computational geometry and single-cell biology.

Gradient Estimation for Binary Latent Variables via Gradient Variance Clipping

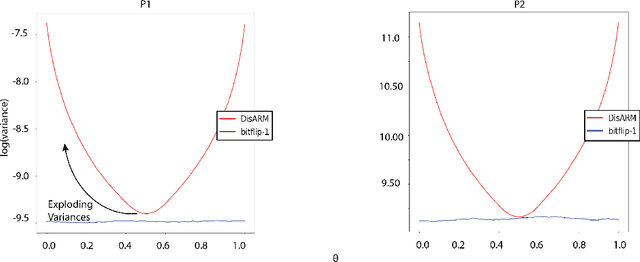
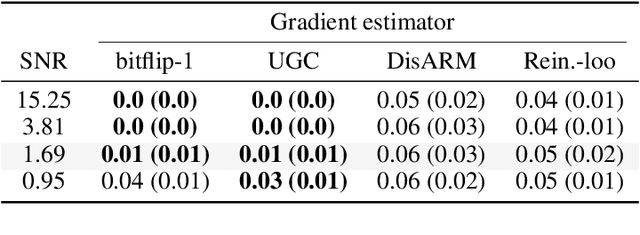
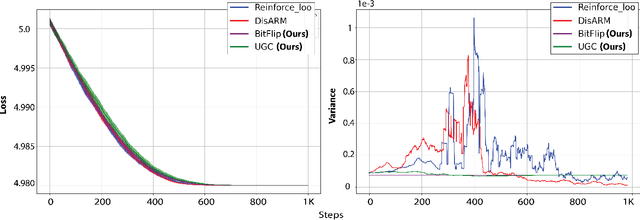
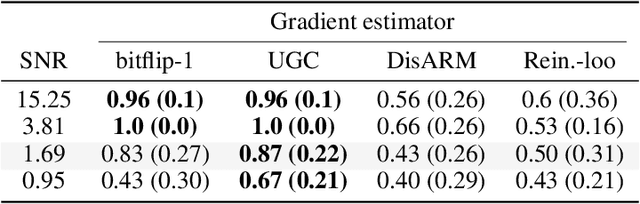
Gradient estimation is often necessary for fitting generative models with discrete latent variables, in contexts such as reinforcement learning and variational autoencoder (VAE) training. The DisARM estimator (Yin et al. 2020; Dong, Mnih, and Tucker 2020) achieves state of the art gradient variance for Bernoulli latent variable models in many contexts. However, DisARM and other estimators have potentially exploding variance near the boundary of the parameter space, where solutions tend to lie. To ameliorate this issue, we propose a new gradient estimator \textit{bitflip}-1 that has lower variance at the boundaries of the parameter space. As bitflip-1 has complementary properties to existing estimators, we introduce an aggregated estimator, \textit{unbiased gradient variance clipping} (UGC) that uses either a bitflip-1 or a DisARM gradient update for each coordinate. We theoretically prove that UGC has uniformly lower variance than DisARM. Empirically, we observe that UGC achieves the optimal value of the optimization objectives in toy experiments, discrete VAE training, and in a best subset selection problem.

MITI Minimum Information guidelines for highly multiplexed tissue images

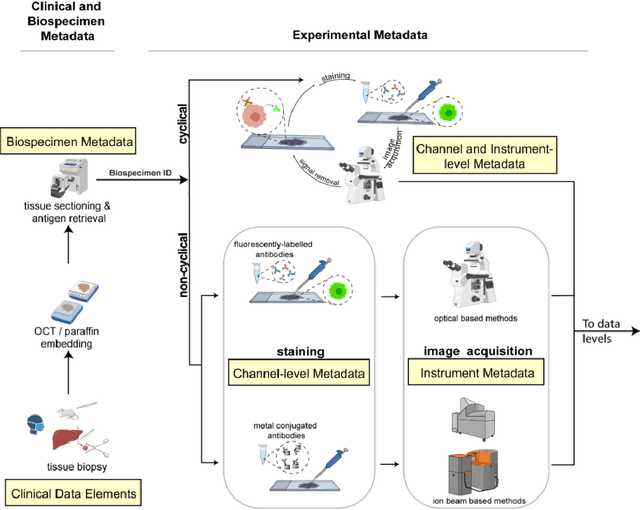
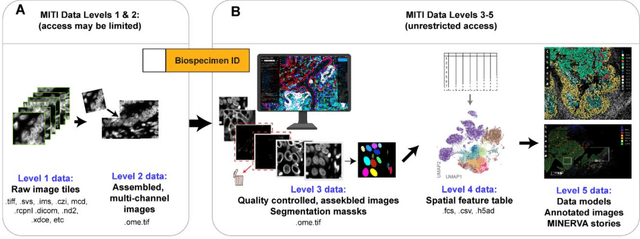
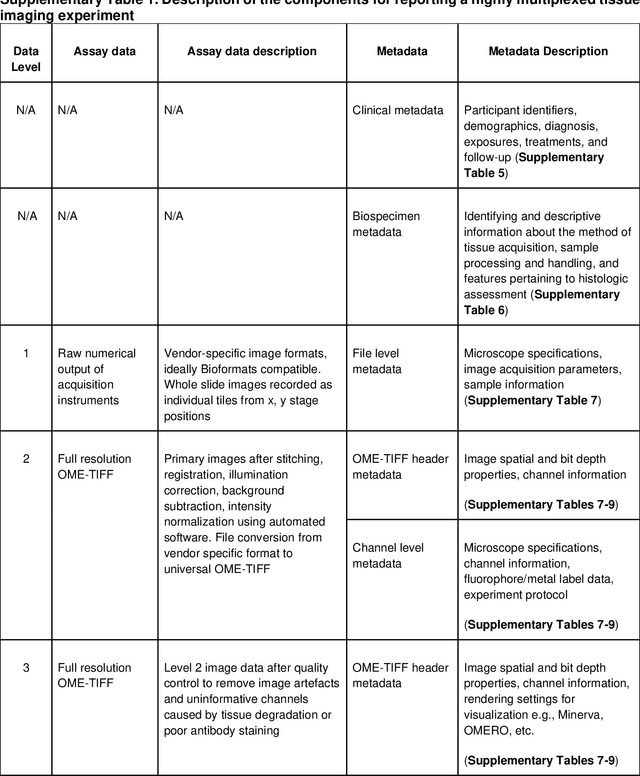
The imminent release of atlases combining highly multiplexed tissue imaging with single cell sequencing and other omics data from human tissues and tumors creates an urgent need for data and metadata standards compliant with emerging and traditional approaches to histology. We describe the development of a Minimum Information about highly multiplexed Tissue Imaging (MITI) standard that draws on best practices from genomics and microscopy of cultured cells and model organisms.

A Nonparametric Multi-view Model for Estimating Cell Type-Specific Gene Regulatory Networks

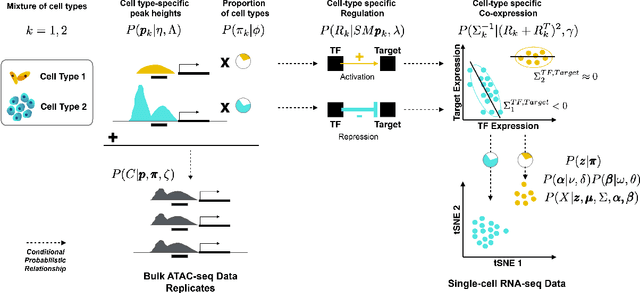
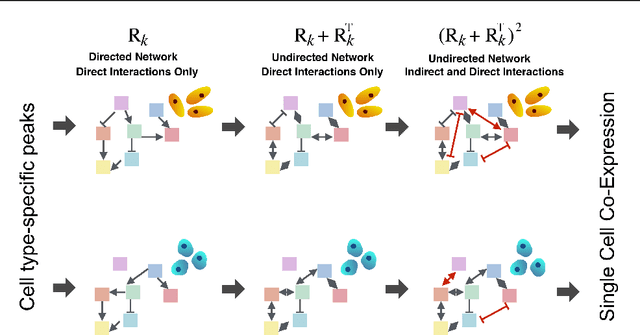
We present a Bayesian hierarchical multi-view mixture model termed Symphony that simultaneously learns clusters of cells representing cell types and their underlying gene regulatory networks by integrating data from two views: single-cell gene expression data and paired epigenetic data, which is informative of gene-gene interactions. This model improves interpretation of clusters as cell types with similar expression patterns as well as regulatory networks driving expression, by explaining gene-gene covariances with the biological machinery regulating gene expression. We show the theoretical advantages of the multi-view learning approach and present a Variational EM inference procedure. We demonstrate superior performance on both synthetic data and real genomic data with subtypes of peripheral blood cells compared to other methods.

Learning Bayesian Network Structure from Massive Datasets: The "Sparse Candidate" Algorithm

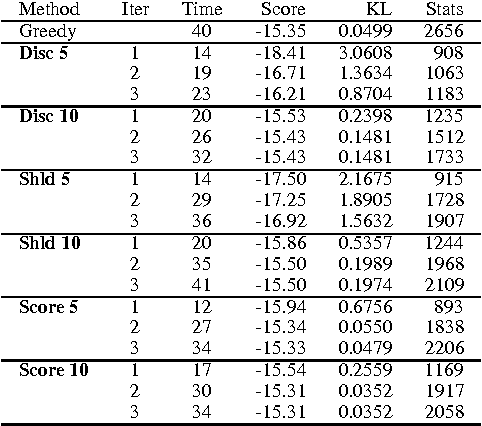
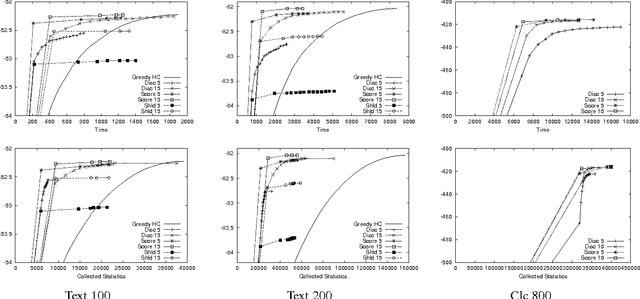
Learning Bayesian networks is often cast as an optimization problem, where the computational task is to find a structure that maximizes a statistically motivated score. By and large, existing learning tools address this optimization problem using standard heuristic search techniques. Since the search space is extremely large, such search procedures can spend most of the time examining candidates that are extremely unreasonable. This problem becomes critical when we deal with data sets that are large either in the number of instances, or the number of attributes. In this paper, we introduce an algorithm that achieves faster learning by restricting the search space. This iterative algorithm restricts the parents of each variable to belong to a small subset of candidates. We then search for a network that satisfies these constraints. The learned network is then used for selecting better candidates for the next iteration. We evaluate this algorithm both on synthetic and real-life data. Our results show that it is significantly faster than alternative search procedures without loss of quality in the learned structures.

Learning Module Networks

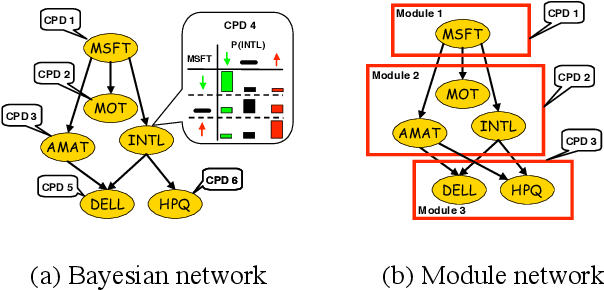
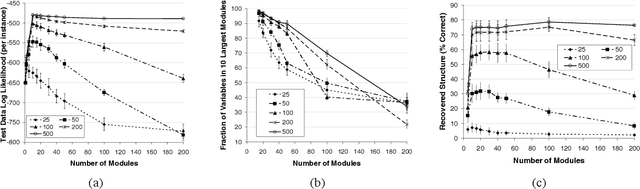
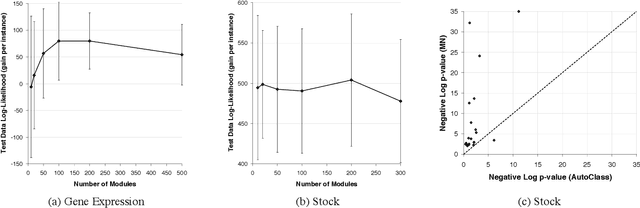
Methods for learning Bayesian network structure can discover dependency structure between observed variables, and have been shown to be useful in many applications. However, in domains that involve a large number of variables, the space of possible network structures is enormous, making it difficult, for both computational and statistical reasons, to identify a good model. In this paper, we consider a solution to this problem, suitable for domains where many variables have similar behavior. Our method is based on a new class of models, which we call module networks. A module network explicitly represents the notion of a module - a set of variables that have the same parents in the network and share the same conditional probability distribution. We define the semantics of module networks, and describe an algorithm that learns a module network from data. The algorithm learns both the partitioning of the variables into modules and the dependency structure between the variables. We evaluate our algorithm on synthetic data, and on real data in the domains of gene expression and the stock market. Our results show that module networks generalize better than Bayesian networks, and that the learned module network structure reveals regularities that are obscured in learned Bayesian networks.