Learning Bayesian Network Structure from Massive Datasets: The "Sparse Candidate" Algorithm

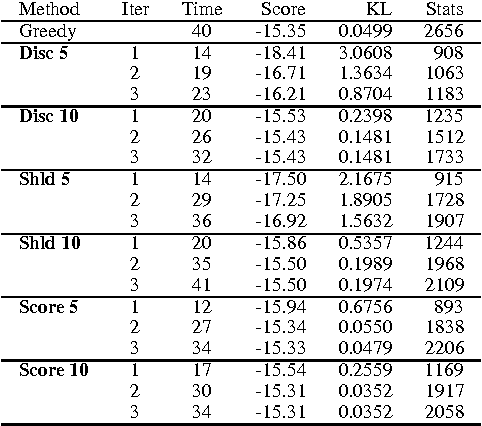
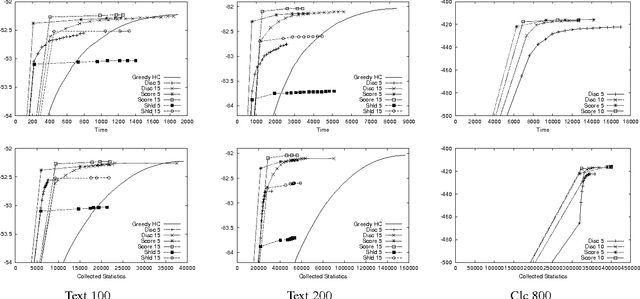
Learning Bayesian networks is often cast as an optimization problem, where the computational task is to find a structure that maximizes a statistically motivated score. By and large, existing learning tools address this optimization problem using standard heuristic search techniques. Since the search space is extremely large, such search procedures can spend most of the time examining candidates that are extremely unreasonable. This problem becomes critical when we deal with data sets that are large either in the number of instances, or the number of attributes. In this paper, we introduce an algorithm that achieves faster learning by restricting the search space. This iterative algorithm restricts the parents of each variable to belong to a small subset of candidates. We then search for a network that satisfies these constraints. The learned network is then used for selecting better candidates for the next iteration. We evaluate this algorithm both on synthetic and real-life data. Our results show that it is significantly faster than alternative search procedures without loss of quality in the learned structures.

Gaussian Process Networks

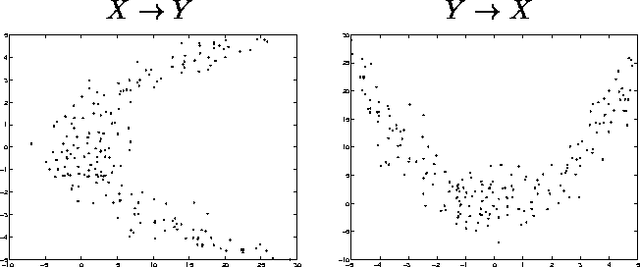
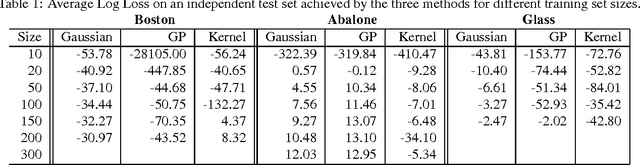
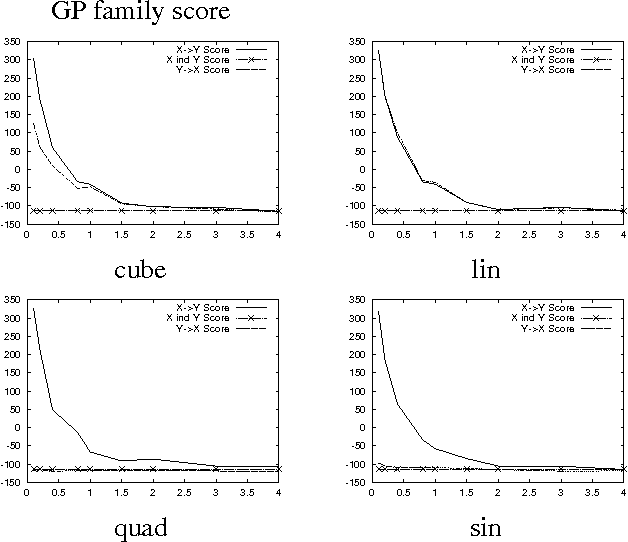
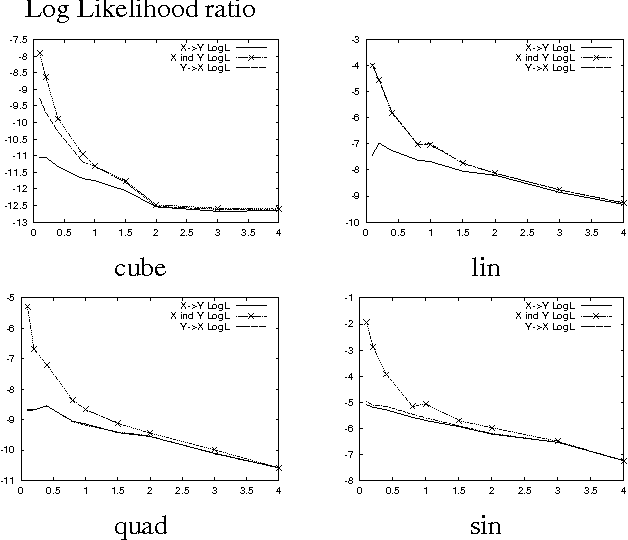
In this paper we address the problem of learning the structure of a Bayesian network in domains with continuous variables. This task requires a procedure for comparing different candidate structures. In the Bayesian framework, this is done by evaluating the {em marginal likelihood/} of the data given a candidate structure. This term can be computed in closed-form for standard parametric families (e.g., Gaussians), and can be approximated, at some computational cost, for some semi-parametric families (e.g., mixtures of Gaussians). We present a new family of continuous variable probabilistic networks that are based on {em Gaussian Process/} priors. These priors are semi-parametric in nature and can learn almost arbitrary noisy functional relations. Using these priors, we can directly compute marginal likelihoods for structure learning. The resulting method can discover a wide range of functional dependencies in multivariate data. We develop the Bayesian score of Gaussian Process Networks and describe how to learn them from data. We present empirical results on artificial data as well as on real-life domains with non-linear dependencies.

"Ideal Parent" Structure Learning for Continuous Variable Networks

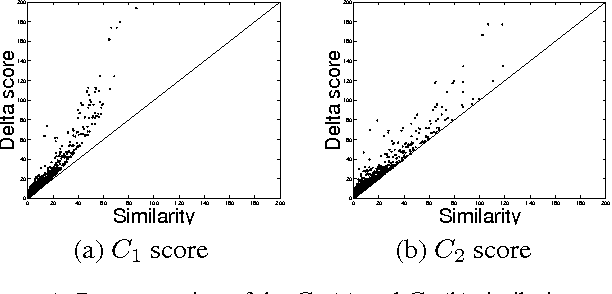
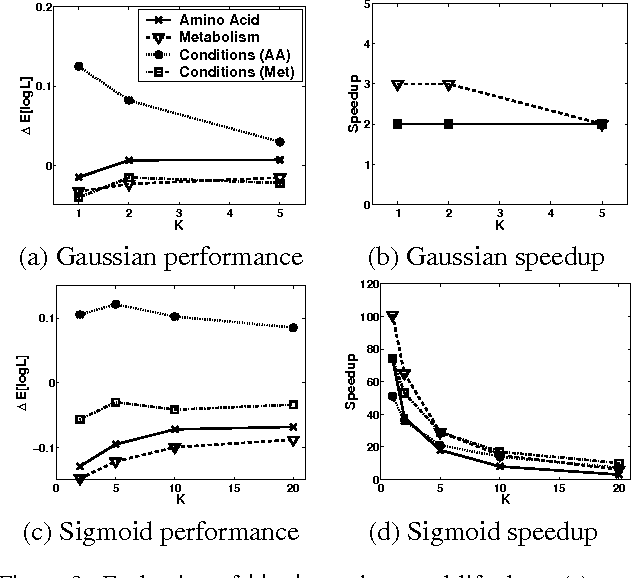
In recent years, there is a growing interest in learning Bayesian networks with continuous variables. Learning the structure of such networks is a computationally expensive procedure, which limits most applications to parameter learning. This problem is even more acute when learning networks with hidden variables. We present a general method for significantly speeding the structure search algorithm for continuous variable networks with common parametric distributions. Importantly, our method facilitates the addition of new hidden variables into the network structure efficiently. We demonstrate the method on several data sets, both for learning structure on fully observable data, and for introducing new hidden variables during structure search.