Learning Module Networks
Paper and Code
Oct 19, 2012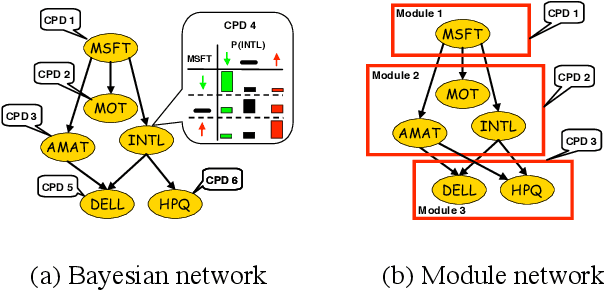
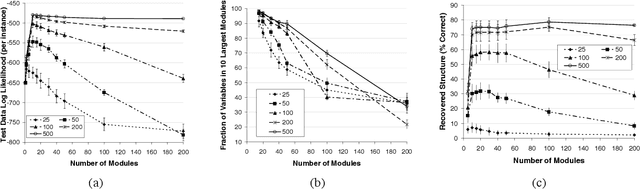
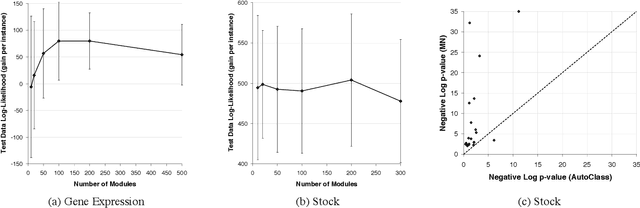
Methods for learning Bayesian network structure can discover dependency structure between observed variables, and have been shown to be useful in many applications. However, in domains that involve a large number of variables, the space of possible network structures is enormous, making it difficult, for both computational and statistical reasons, to identify a good model. In this paper, we consider a solution to this problem, suitable for domains where many variables have similar behavior. Our method is based on a new class of models, which we call module networks. A module network explicitly represents the notion of a module - a set of variables that have the same parents in the network and share the same conditional probability distribution. We define the semantics of module networks, and describe an algorithm that learns a module network from data. The algorithm learns both the partitioning of the variables into modules and the dependency structure between the variables. We evaluate our algorithm on synthetic data, and on real data in the domains of gene expression and the stock market. Our results show that module networks generalize better than Bayesian networks, and that the learned module network structure reveals regularities that are obscured in learned Bayesian networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge