Local Reactive Control for Mobile Manipulators with Whole-Body Safety in Complex Environments

Mobile manipulators typically encounter significant challenges in navigating narrow, cluttered environments due to their high-dimensional state spaces and complex kinematics. While reactive methods excel in dynamic settings, they struggle to efficiently incorporate complex, coupled constraints across the entire state space. In this work, we present a novel local reactive controller that reformulates the time-domain single-step problem into a multi-step optimization problem in the spatial domain, leveraging the propagation of a serial kinematic chain. This transformation facilitates the formulation of customized, decoupled link-specific constraints, which is further solved efficiently with augmented Lagrangian differential dynamic programming (AL-DDP). Our approach naturally absorbs spatial kinematic propagation in the forward pass and processes all link-specific constraints simultaneously during the backward pass, enhancing both constraint management and computational efficiency. Notably, in this framework, we formulate collision avoidance constraints for each link using accurate geometric models with extracted free regions, and this improves the maneuverability of the mobile manipulator in narrow, cluttered spaces. Experimental results showcase significant improvements in safety, efficiency, and task completion rates. These findings underscore the robustness of the proposed method, particularly in narrow, cluttered environments where conventional approaches could falter. The open-source project can be found at https://github.com/Chunx1nZHENG/MM-with-Whole-Body-Safety-Release.git.

FRTree Planner: Robot Navigation in Cluttered and Unknown Environments with Tree of Free Regions

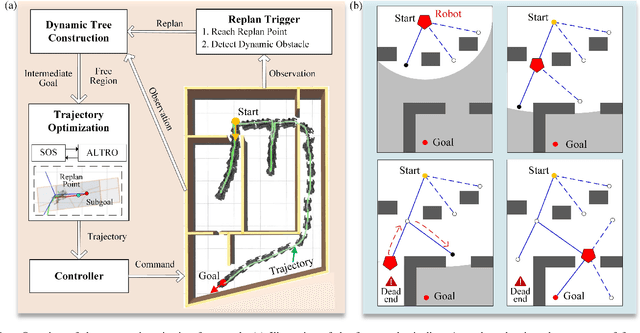
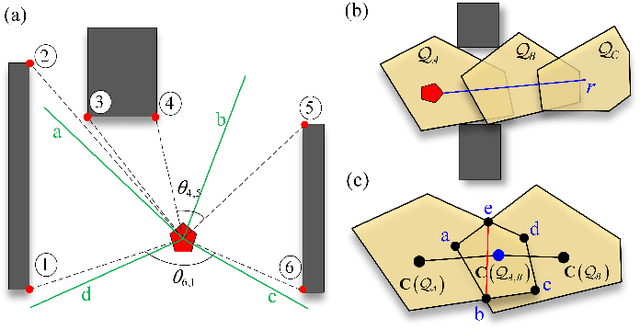
In this work, we present FRTree planner, a novel robot navigation framework that leverages a tree structure of free regions, specifically designed for navigation in cluttered and unknown environments with narrow passages. The framework continuously incorporates real-time perceptive information to identify distinct navigation options and dynamically expands the tree toward explorable and traversable directions. This dynamically constructed tree incrementally encodes the geometric and topological information of the collision-free space, enabling efficient selection of the intermediate goals, navigating around dead-end situations, and avoidance of dynamic obstacles without a prior map. Crucially, our method performs a comprehensive analysis of the geometric relationship between free regions and the robot during online replanning. In particular, the planner assesses the accessibility of candidate passages based on the robot's geometries, facilitating the effective selection of the most viable intermediate goals through accessible narrow passages while minimizing unnecessary detours. By combining the free region information with a bi-level trajectory optimization tailored for robots with specific geometries, our approach generates robust and adaptable obstacle avoidance strategies in confined spaces. Through extensive simulations and real-world experiments, FRTree demonstrates its superiority over benchmark methods in generating safe, efficient motion plans through highly cluttered and unknown terrains with narrow gaps.

Collision-Free Trajectory Optimization in Cluttered Environments with Sums-of-Squares Programming

In this work, we propose a trajectory optimization approach for robot navigation in cluttered 3D environments. We represent the robot's geometry as a semialgebraic set defined by polynomial inequalities such that robots with general shapes can be suitably characterized. To address the robot navigation task in obstacle-dense environments, we exploit the free space directly to construct a sequence of free regions, and allocate each waypoint on the trajectory to a specific region. Then, we incorporate a uniform scaling factor for each free region, and formulate a Sums-of-Squares (SOS) optimization problem that renders the containment relationship between the robot and the free space computationally tractable. The SOS optimization problem is further reformulated to a semidefinite program (SDP), and the collision-free constraints are shown to be equivalent to limiting the scaling factor along the entire trajectory. In this context, the robot at a specific configuration is tailored to stay within the free region. Next, to solve the trajectory optimization problem with the proposed safety constraints (which are implicitly dependent on the robot configurations), we derive the analytical solution to the gradient of the minimum scaling factor with respect to the robot configuration. As a result, this seamlessly facilitates the use of gradient-based methods in efficient solving of the trajectory optimization problem. Through a series of simulations and real-world experiments, the proposed trajectory optimization approach is validated in various challenging scenarios, and the results demonstrate its effectiveness in generating collision-free trajectories in dense and intricate environments populated with obstacles.

Geometry-Aware Safety-Critical Local Reactive Controller for Robot Navigation in Unknown and Cluttered Environments

This work proposes a safety-critical local reactive controller that enables the robot to navigate in unknown and cluttered environments. In particular, the trajectory tracking task is formulated as a constrained polynomial optimization problem. Then, safety constraints are imposed on the control variables invoking the notion of polynomial positivity certificates in conjunction with their Sum-of-Squares (SOS) approximation, thereby confining the robot motion inside the locally extracted convex free region. It is noteworthy that, in the process of devising the proposed safety constraints, the geometry of the robot can be approximated using any shape that can be characterized with a set of polynomial functions. The optimization problem is further convexified into a semidefinite program (SDP) leveraging truncated multi-sequences (tms) and moment relaxation, which favorably facilitates the effective use of off-the-shelf conic programming solvers, such that real-time performance is attainable. Various robot navigation tasks are investigated to demonstrate the effectiveness of the proposed approach in terms of safety and tracking performance.