Thought-Augmented Policy Optimization: Bridging External Guidance and Internal Capabilities

Reinforcement learning (RL) has emerged as an effective method for training reasoning models. However, existing RL approaches typically bias the model's output distribution toward reward-maximizing paths without introducing external knowledge. This limits their exploration capacity and results in a narrower reasoning capability boundary compared to base models. To address this limitation, we propose TAPO (Thought-Augmented Policy Optimization), a novel framework that augments RL by incorporating external high-level guidance ("thought patterns"). By adaptively integrating structured thoughts during training, TAPO effectively balances model-internal exploration and external guidance exploitation. Extensive experiments show that our approach significantly outperforms GRPO by 99% on AIME, 41% on AMC, and 17% on Minerva Math. Notably, these high-level thought patterns, abstracted from only 500 prior samples, generalize effectively across various tasks and models. This highlights TAPO's potential for broader applications across multiple tasks and domains. Our further analysis reveals that introducing external guidance produces powerful reasoning models with superior explainability of inference behavior and enhanced output readability.

Exploring Forgetting in Large Language Model Pre-Training

Catastrophic forgetting remains a formidable obstacle to building an omniscient model in large language models (LLMs). Despite the pioneering research on task-level forgetting in LLM fine-tuning, there is scant focus on forgetting during pre-training. We systematically explored the existence and measurement of forgetting in pre-training, questioning traditional metrics such as perplexity (PPL) and introducing new metrics to better detect entity memory retention. Based on our revised assessment of forgetting metrics, we explored low-cost, straightforward methods to mitigate forgetting during the pre-training phase. Further, we carefully analyzed the learning curves, offering insights into the dynamics of forgetting. Extensive evaluations and analyses on forgetting of pre-training could facilitate future research on LLMs.

Improving Discriminative Multi-Modal Learning with Large-Scale Pre-Trained Models

This paper investigates how to better leverage large-scale pre-trained uni-modal models to further enhance discriminative multi-modal learning. Even when fine-tuned with only uni-modal data, these models can outperform previous multi-modal models in certain tasks. It's clear that their incorporation into multi-modal learning would significantly improve performance. However, multi-modal learning with these models still suffers from insufficient learning of uni-modal features, which weakens the resulting multi-modal model's generalization ability. While fine-tuning uni-modal models separately and then aggregating their predictions is straightforward, it doesn't allow for adequate adaptation between modalities, also leading to sub-optimal results. To this end, we introduce Multi-Modal Low-Rank Adaptation learning (MMLoRA). By freezing the weights of uni-modal fine-tuned models, adding extra trainable rank decomposition matrices to them, and subsequently performing multi-modal joint training, our method enhances adaptation between modalities and boosts overall performance. We demonstrate the effectiveness of MMLoRA on three dataset categories: audio-visual (e.g., AVE, Kinetics-Sound, CREMA-D), vision-language (e.g., MM-IMDB, UPMC Food101), and RGB-Optical Flow (UCF101).

Zero-Label Prompt Selection

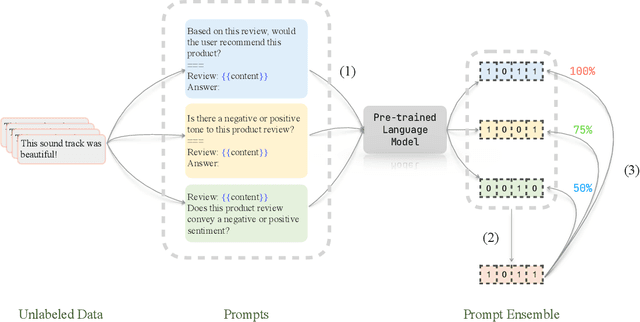
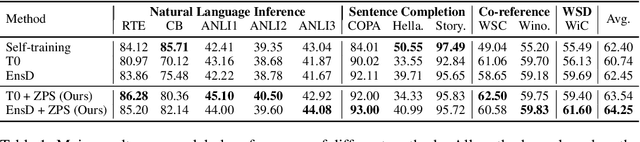
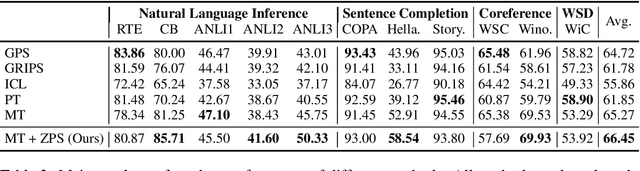
Natural language prompts have been shown to facilitate cross-task generalization for large language models. However, with no or limited labeled examples, the cross-task performance is highly sensitive to the choice of prompts, while selecting a high-performing prompt is challenging given the scarcity of labels. To address the issue, we propose a Zero-Label Prompt Selection (ZPS) method that selects prompts without any labeled data or gradient update. Specifically, given the candidate human-written prompts for a task, ZPS labels a set of unlabeled data with a prompt ensemble and uses the pseudo-labels for prompt selection. Experiments show that ZPS improves over prior methods by a sizeable margin in zero-label performance. We also extend ZPS to a few-shot setting and show its advantages over strong baselines such as prompt tuning and model tuning.

Locally Differentially Private Reinforcement Learning for Linear Mixture Markov Decision Processes

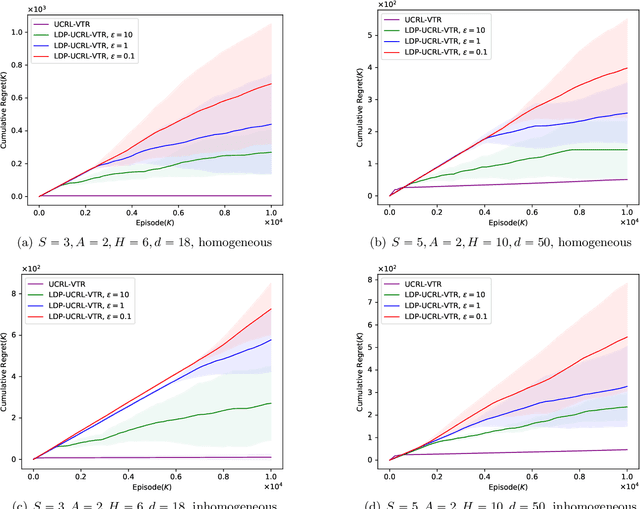
Reinforcement learning (RL) algorithms can be used to provide personalized services, which rely on users' private and sensitive data. To protect the users' privacy, privacy-preserving RL algorithms are in demand. In this paper, we study RL with linear function approximation and local differential privacy (LDP) guarantees. We propose a novel $(\varepsilon, \delta)$-LDP algorithm for learning a class of Markov decision processes (MDPs) dubbed linear mixture MDPs, and obtains an $\tilde{\mathcal{O}}( d^{5/4}H^{7/4}T^{3/4}\left(\log(1/\delta)\right)^{1/4}\sqrt{1/\varepsilon})$ regret, where $d$ is the dimension of feature mapping, $H$ is the length of the planning horizon, and $T$ is the number of interactions with the environment. We also prove a lower bound $\Omega(dH\sqrt{T}/\left(e^{\varepsilon}(e^{\varepsilon}-1)\right))$ for learning linear mixture MDPs under $\varepsilon$-LDP constraint. Experiments on synthetic datasets verify the effectiveness of our algorithm. To the best of our knowledge, this is the first provable privacy-preserving RL algorithm with linear function approximation.