Locally Differentially Private Reinforcement Learning for Linear Mixture Markov Decision Processes
Paper and Code
Oct 19, 2021
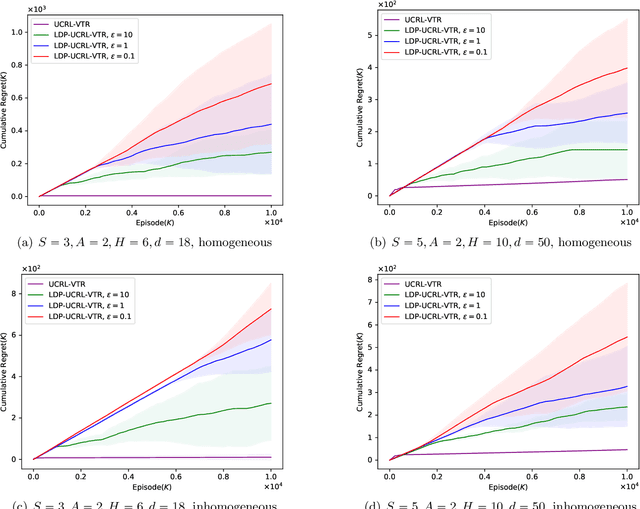
Reinforcement learning (RL) algorithms can be used to provide personalized services, which rely on users' private and sensitive data. To protect the users' privacy, privacy-preserving RL algorithms are in demand. In this paper, we study RL with linear function approximation and local differential privacy (LDP) guarantees. We propose a novel $(\varepsilon, \delta)$-LDP algorithm for learning a class of Markov decision processes (MDPs) dubbed linear mixture MDPs, and obtains an $\tilde{\mathcal{O}}( d^{5/4}H^{7/4}T^{3/4}\left(\log(1/\delta)\right)^{1/4}\sqrt{1/\varepsilon})$ regret, where $d$ is the dimension of feature mapping, $H$ is the length of the planning horizon, and $T$ is the number of interactions with the environment. We also prove a lower bound $\Omega(dH\sqrt{T}/\left(e^{\varepsilon}(e^{\varepsilon}-1)\right))$ for learning linear mixture MDPs under $\varepsilon$-LDP constraint. Experiments on synthetic datasets verify the effectiveness of our algorithm. To the best of our knowledge, this is the first provable privacy-preserving RL algorithm with linear function approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge