Generating and designing DNA with deep generative models

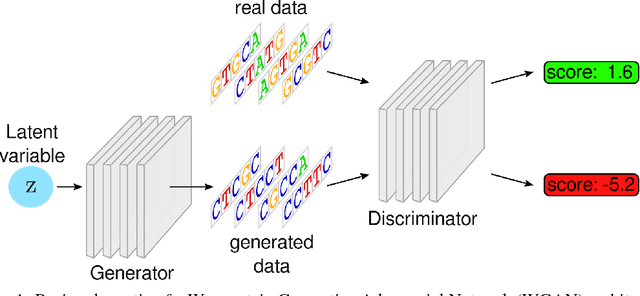
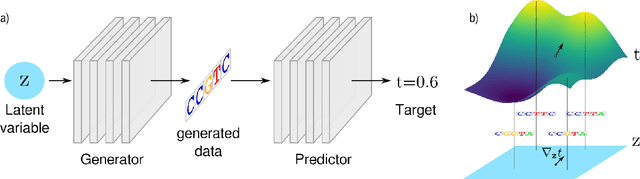
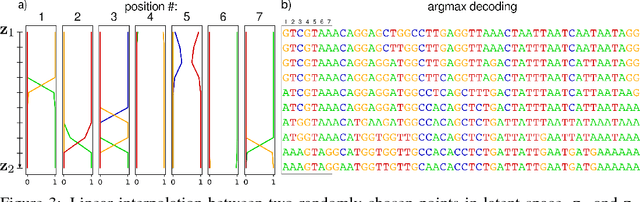
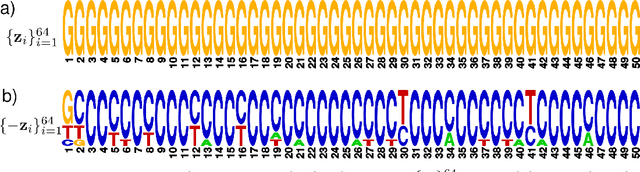
We propose generative neural network methods to generate DNA sequences and tune them to have desired properties. We present three approaches: creating synthetic DNA sequences using a generative adversarial network; a DNA-based variant of the activation maximization ("deep dream") design method; and a joint procedure which combines these two approaches together. We show that these tools capture important structures of the data and, when applied to designing probes for protein binding microarrays, allow us to generate new sequences whose properties are estimated to be superior to those found in the training data. We believe that these results open the door for applying deep generative models to advance genomics research.

Variational Learning in Mixed-State Dynamic Graphical Models

Many real-valued stochastic time-series are locally linear (Gassian), but globally non-linear. For example, the trajectory of a human hand gesture can be viewed as a linear dynamic system driven by a nonlinear dynamic system that represents muscle actions. We present a mixed-state dynamic graphical model in which a hidden Markov model drives a linear dynamic system. This combination allows us to model both the discrete and continuous causes of trajectories such as human gestures. The number of computations needed for exact inference is exponential in the sequence length, so we derive an approximate variational inference technique that can also be used to learn the parameters of the discrete and continuous models. We show how the mixed-state model and the variational technique can be used to classify human hand gestures made with a computer mouse.

Learning Graphical Models of Images, Videos and Their Spatial Transformations

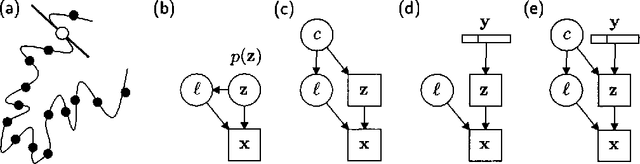
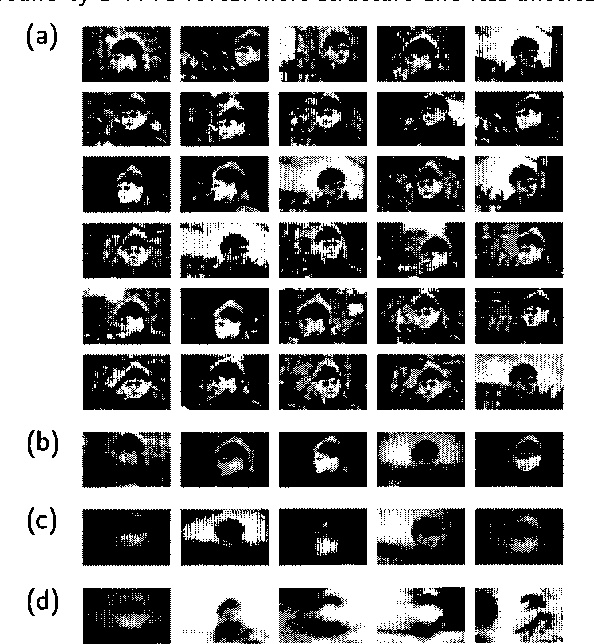
Mixtures of Gaussians, factor analyzers (probabilistic PCA) and hidden Markov models are staples of static and dynamic data modeling and image and video modeling in particular. We show how topographic transformations in the input, such as translation and shearing in images, can be accounted for in these models by including a discrete transformation variable. The resulting models perform clustering, dimensionality reduction and time-series analysis in a way that is invariant to transformations in the input. Using the EM algorithm, these transformation-invariant models can be fit to static data and time series. We give results on filtering microscopy images, face and facial pose clustering, handwritten digit modeling and recognition, video clustering, object tracking, and removal of distractions from video sequences.

A Factorized Variational Technique for Phase Unwrapping in Markov Random Fields

Some types of medical and topographic imaging device produce images in which the pixel values are "phase-wrapped", i.e. measured modulus a known scalar. Phase unwrapping can be viewed as the problem of inferring the number of shifts between each and every pair of neighboring pixels, subject to an a priori preference for smooth surfaces, and subject to a zero curl constraint, which requires that the shifts must sum to 0 around every loop. We formulate phase unwrapping as a mean field inference problem in a Markov network, where the prior favors the zero curl constraint. We compare our mean field technique with the least squares method on a synthetic 100x100 image, and give results on a 512x512 synthetic aperture radar image from Sandia National Laboratories.<Long Text>

Learning Generative Models of Similarity Matrices

We describe a probabilistic (generative) view of affinity matrices along with inference algorithms for a subclass of problems associated with data clustering. This probabilistic view is helpful in understanding different models and algorithms that are based on affinity functions OF the data. IN particular, we show how(greedy) inference FOR a specific probabilistic model IS equivalent TO the spectral clustering algorithm.It also provides a framework FOR developing new algorithms AND extended models. AS one CASE, we present new generative data clustering models that allow us TO infer the underlying distance measure suitable for the clustering problem at hand. These models seem to perform well in a larger class of problems for which other clustering algorithms (including spectral clustering) usually fail. Experimental evaluation was performed in a variety point data sets, showing excellent performance.

Extending Factor Graphs so as to Unify Directed and Undirected Graphical Models

The two most popular types of graphical model are directed models (Bayesian networks) and undirected models (Markov random fields, or MRFs). Directed and undirected models offer complementary properties in model construction, expressing conditional independencies, expressing arbitrary factorizations of joint distributions, and formulating message-passing inference algorithms. We show that the strengths of these two representations can be combined in a single type of graphical model called a 'factor graph'. Every Bayesian network or MRF can be easily converted to a factor graph that expresses the same conditional independencies, expresses the same factorization of the joint distribution, and can be used for probabilistic inference through application of a single, simple message-passing algorithm. In contrast to chain graphs, where message-passing is implemented on a hypergraph, message-passing can be directly implemented on the factor graph. We describe a modified 'Bayes-ball' algorithm for establishing conditional independence in factor graphs, and we show that factor graphs form a strict superset of Bayesian networks and MRFs. In particular, we give an example of a commonly-used 'mixture of experts' model fragment, whose independencies cannot be represented in a Bayesian network or an MRF, but can be represented in a factor graph. We finish by giving examples of real-world problems that are not well suited to representation in Bayesian networks and MRFs, but are well-suited to representation in factor graphs.

Fast Exact Inference for Recursive Cardinality Models

Cardinality potentials are a generally useful class of high order potential that affect probabilities based on how many of D binary variables are active. Maximum a posteriori (MAP) inference for cardinality potential models is well-understood, with efficient computations taking O(DlogD) time. Yet efficient marginalization and sampling have not been addressed as thoroughly in the machine learning community. We show that there exists a simple algorithm for computing marginal probabilities and drawing exact joint samples that runs in O(Dlog2 D) time, and we show how to frame the algorithm as efficient belief propagation in a low order tree-structured model that includes additional auxiliary variables. We then develop a new, more general class of models, termed Recursive Cardinality models, which take advantage of this efficiency. Finally, we show how to do efficient exact inference in models composed of a tree structure and a cardinality potential. We explore the expressive power of Recursive Cardinality models and empirically demonstrate their utility.

Convolutional Factor Graphs as Probabilistic Models

Based on a recent development in the area of error control coding, we introduce the notion of convolutional factor graphs (CFGs) as a new class of probabilistic graphical models. In this context, the conventional factor graphs are referred to as multiplicative factor graphs (MFGs). This paper shows that CFGs are natural models for probability functions when summation of independent latent random variables is involved. In particular, CFGs capture a large class of linear models, where the linearity is in the sense that the observed variables are obtained as a linear ransformation of the latent variables taking arbitrary distributions. We use Gaussian models and independent factor models as examples to emonstrate the use of CFGs. The requirement of a linear transformation between latent variables (with certain independence restriction) and the bserved variables, to an extent, limits the modelling flexibility of CFGs. This structural restriction however provides a powerful analytic tool to the framework of CFGs; that is, upon taking the Fourier transform of the function represented by the CFG, the resulting function is represented by a FG with identical structure. This Fourier transform duality allows inference problems on a CFG to be solved on the corresponding dual MFG.

Matrix Tile Analysis

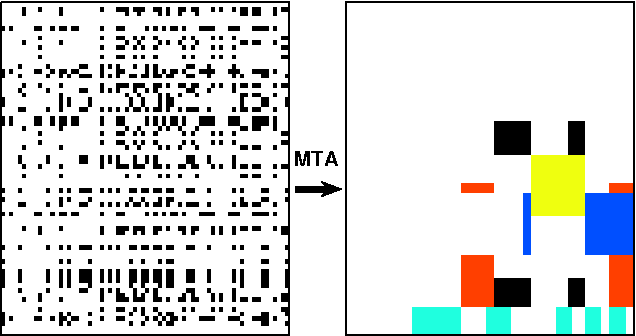
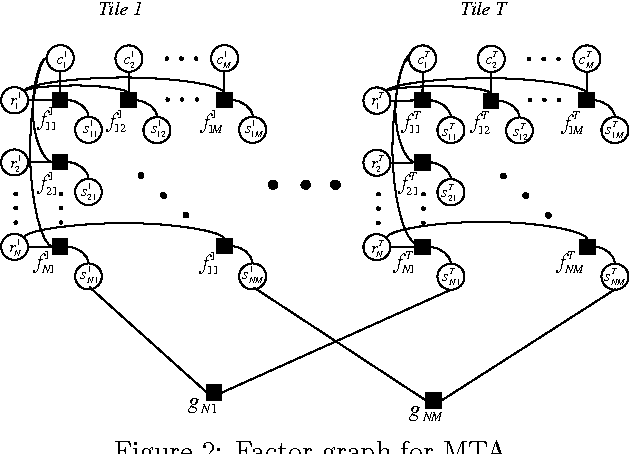
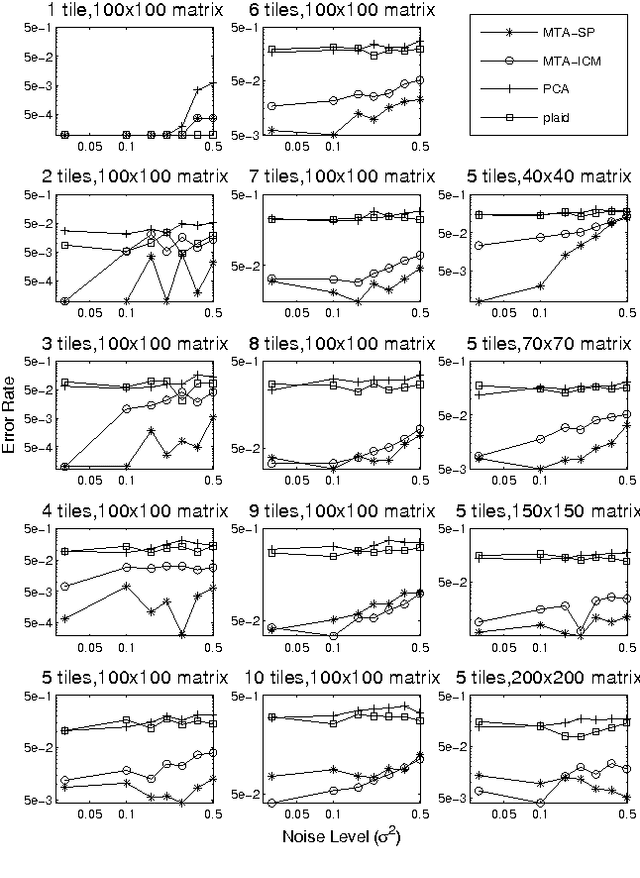
Many tasks require finding groups of elements in a matrix of numbers, symbols or class likelihoods. One approach is to use efficient bi- or tri-linear factorization techniques including PCA, ICA, sparse matrix factorization and plaid analysis. These techniques are not appropriate when addition and multiplication of matrix elements are not sensibly defined. More directly, methods like bi-clustering can be used to classify matrix elements, but these methods make the overly-restrictive assumption that the class of each element is a function of a row class and a column class. We introduce a general computational problem, `matrix tile analysis' (MTA), which consists of decomposing a matrix into a set of non-overlapping tiles, each of which is defined by a subset of usually nonadjacent rows and columns. MTA does not require an algebra for combining tiles, but must search over discrete combinations of tile assignments. Exact MTA is a computationally intractable integer programming problem, but we describe an approximate iterative technique and a computationally efficient sum-product relaxation of the integer program. We compare the effectiveness of these methods to PCA and plaid on hundreds of randomly generated tasks. Using double-gene-knockout data, we show that MTA finds groups of interacting yeast genes that have biologically-related functions.

Flexible Priors for Exemplar-based Clustering

Exemplar-based clustering methods have been shown to produce state-of-the-art results on a number of synthetic and real-world clustering problems. They are appealing because they offer computational benefits over latent-mean models and can handle arbitrary pairwise similarity measures between data points. However, when trying to recover underlying structure in clustering problems, tailored similarity measures are often not enough; we also desire control over the distribution of cluster sizes. Priors such as Dirichlet process priors allow the number of clusters to be unspecified while expressing priors over data partitions. To our knowledge, they have not been applied to exemplar-based models. We show how to incorporate priors, including Dirichlet process priors, into the recently introduced affinity propagation algorithm. We develop an efficient maxproduct belief propagation algorithm for our new model and demonstrate experimentally how the expanded range of clustering priors allows us to better recover true clusterings in situations where we have some information about the generating process.