Learning Linear Programs from Optimal Decisions

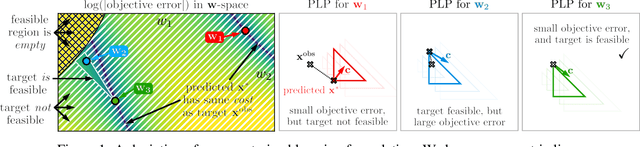
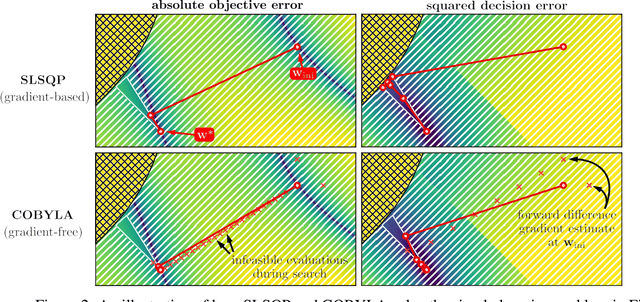
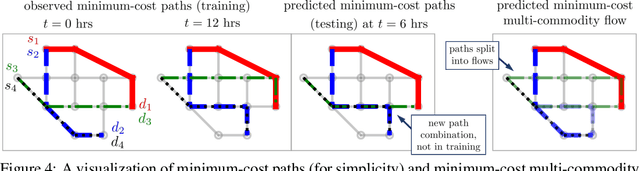
We propose a flexible gradient-based framework for learning linear programs from optimal decisions. Linear programs are often specified by hand, using prior knowledge of relevant costs and constraints. In some applications, linear programs must instead be learned from observations of optimal decisions. Learning from optimal decisions is a particularly challenging bi-level problem, and much of the related inverse optimization literature is dedicated to special cases. We tackle the general problem, learning all parameters jointly while allowing flexible parametrizations of costs, constraints, and loss functions. We also address challenges specific to learning linear programs, such as empty feasible regions and non-unique optimal decisions. Experiments show that our method successfully learns synthetic linear programs and minimum-cost multi-commodity flow instances for which previous methods are not directly applicable. We also provide a fast batch-mode PyTorch implementation of the homogeneous interior point algorithm, which supports gradients by implicit differentiation or backpropagation.

Deep Inverse Optimization

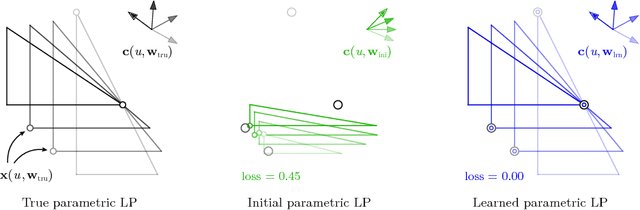
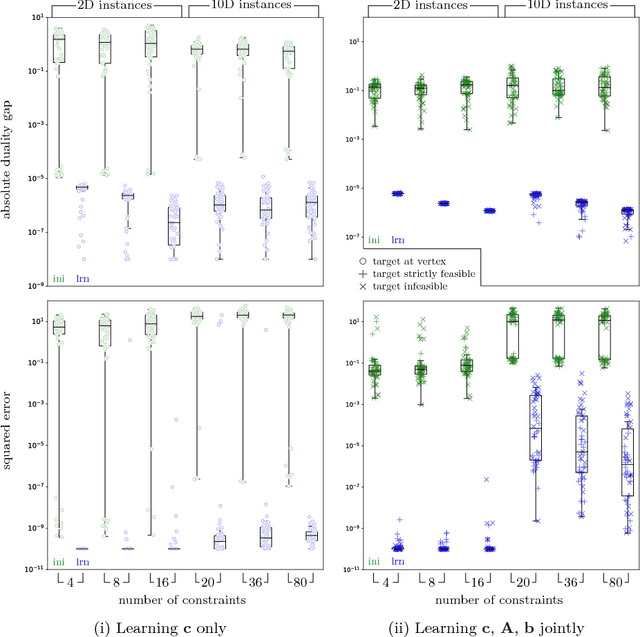
Given a set of observations generated by an optimization process, the goal of inverse optimization is to determine likely parameters of that process. We cast inverse optimization as a form of deep learning. Our method, called deep inverse optimization, is to unroll an iterative optimization process and then use backpropagation to learn parameters that generate the observations. We demonstrate that by backpropagating through the interior point algorithm we can learn the coefficients determining the cost vector and the constraints, independently or jointly, for both non-parametric and parametric linear programs, starting from one or multiple observations. With this approach, inverse optimization can leverage concepts and algorithms from deep learning.

Generating and designing DNA with deep generative models

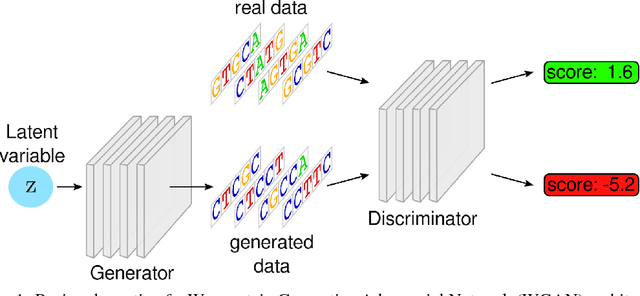
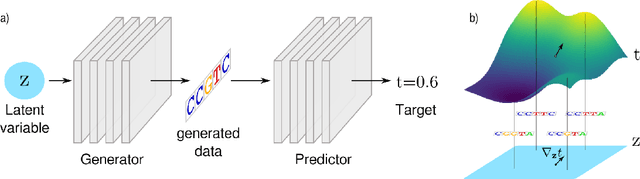
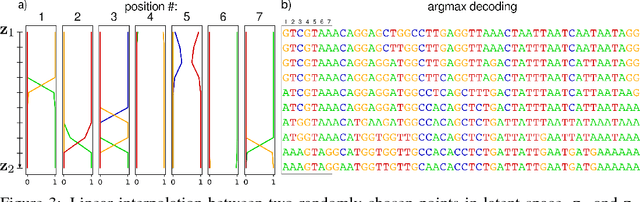
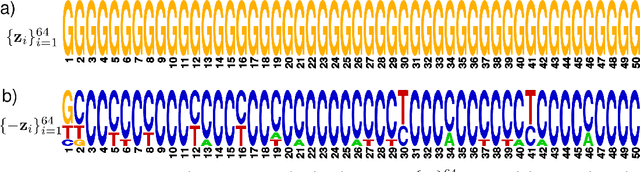
We propose generative neural network methods to generate DNA sequences and tune them to have desired properties. We present three approaches: creating synthetic DNA sequences using a generative adversarial network; a DNA-based variant of the activation maximization ("deep dream") design method; and a joint procedure which combines these two approaches together. We show that these tools capture important structures of the data and, when applied to designing probes for protein binding microarrays, allow us to generate new sequences whose properties are estimated to be superior to those found in the training data. We believe that these results open the door for applying deep generative models to advance genomics research.

Submodularization for Quadratic Pseudo-Boolean Optimization

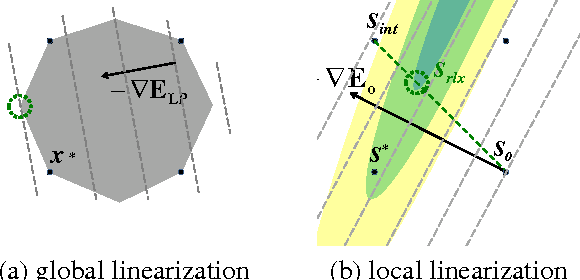
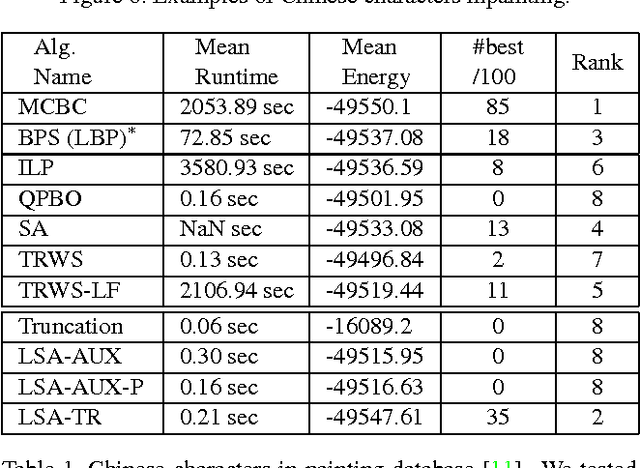
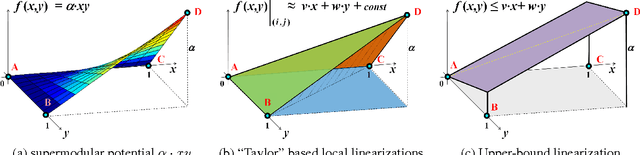
Many computer vision problems require optimization of binary non-submodular energies. We propose a general optimization framework based on local submodular approximations (LSA). Unlike standard LP relaxation methods that linearize the whole energy globally, our approach iteratively approximates the energies locally. On the other hand, unlike standard local optimization methods (e.g. gradient descent or projection techniques) we use non-linear submodular approximations and optimize them without leaving the domain of integer solutions. We discuss two specific LSA algorithms based on "trust region" and "auxiliary function" principles, LSA-TR and LSA-AUX. These methods obtain state-of-the-art results on a wide range of applications outperforming many standard techniques such as LBP, QPBO, and TRWS. While our paper is focused on pairwise energies, our ideas extend to higher-order problems. The code is available online (http://vision.csd.uwo.ca/code/).