Learning Linear Programs from Optimal Decisions

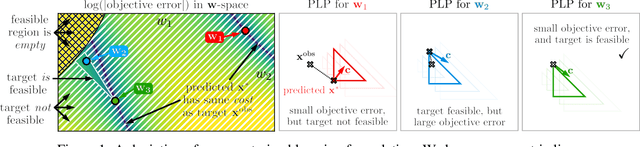
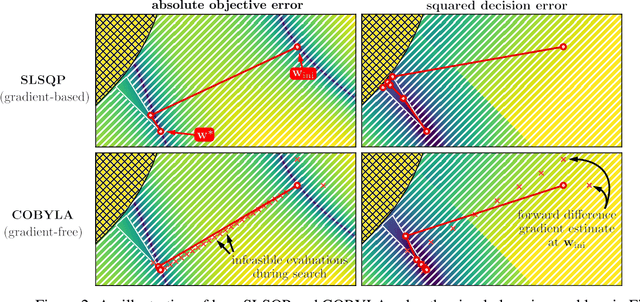
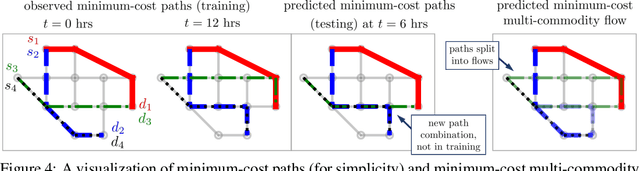
We propose a flexible gradient-based framework for learning linear programs from optimal decisions. Linear programs are often specified by hand, using prior knowledge of relevant costs and constraints. In some applications, linear programs must instead be learned from observations of optimal decisions. Learning from optimal decisions is a particularly challenging bi-level problem, and much of the related inverse optimization literature is dedicated to special cases. We tackle the general problem, learning all parameters jointly while allowing flexible parametrizations of costs, constraints, and loss functions. We also address challenges specific to learning linear programs, such as empty feasible regions and non-unique optimal decisions. Experiments show that our method successfully learns synthetic linear programs and minimum-cost multi-commodity flow instances for which previous methods are not directly applicable. We also provide a fast batch-mode PyTorch implementation of the homogeneous interior point algorithm, which supports gradients by implicit differentiation or backpropagation.

Deep Inverse Optimization

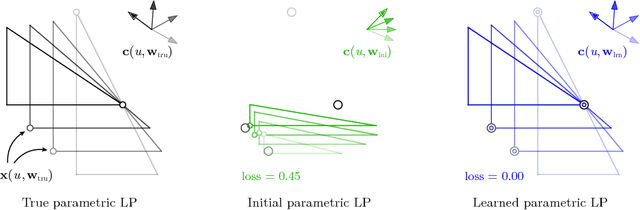
Given a set of observations generated by an optimization process, the goal of inverse optimization is to determine likely parameters of that process. We cast inverse optimization as a form of deep learning. Our method, called deep inverse optimization, is to unroll an iterative optimization process and then use backpropagation to learn parameters that generate the observations. We demonstrate that by backpropagating through the interior point algorithm we can learn the coefficients determining the cost vector and the constraints, independently or jointly, for both non-parametric and parametric linear programs, starting from one or multiple observations. With this approach, inverse optimization can leverage concepts and algorithms from deep learning.

A Constraint Programming Approach for Solving a Queueing Control Problem

In a facility with front room and back room operations, it is useful to switch workers between the rooms in order to cope with changing customer demand. Assuming stochastic customer arrival and service times, we seek a policy for switching workers such that the expected customer waiting time is minimized while the expected back room staffing is sufficient to perform all work. Three novel constraint programming models and several shaving procedures for these models are presented. Experimental results show that a model based on closed-form expressions together with a combination of shaving procedures is the most efficient. This model is able to find and prove optimal solutions for many problem instances within a reasonable run-time. Previously, the only available approach was a heuristic algorithm. Furthermore, a hybrid method combining the heuristic and the best constraint programming method is shown to perform as well as the heuristic in terms of solution quality over time, while achieving the same performance in terms of proving optimality as the pure constraint programming model. This is the first work of which we are aware that solves such queueing-based problems with constraint programming.