Domain-Independent Dynamic Programming

For combinatorial optimization problems, model-based paradigms such as mixed-integer programming (MIP) and constraint programming (CP) aim to decouple modeling and solving a problem: the `holy grail' of declarative problem solving. We propose domain-independent dynamic programming (DIDP), a new model-based paradigm based on dynamic programming (DP). While DP is not new, it has typically been implemented as a problem-specific method. We introduce Dynamic Programming Description Language (DyPDL), a formalism to define DP models based on a state transition system, inspired by AI planning. We show that heuristic search algorithms can be used to solve DyPDL models and propose seven DIDP solvers. We experimentally compare our DIDP solvers with commercial MIP and CP solvers (solving MIP and CP models, respectively) on common benchmark instances of eleven combinatorial optimization problem classes. We show that DIDP outperforms MIP in nine problem classes, CP also in nine problem classes, and both MIP and CP in seven.

PRP Rebooted: Advancing the State of the Art in FOND Planning

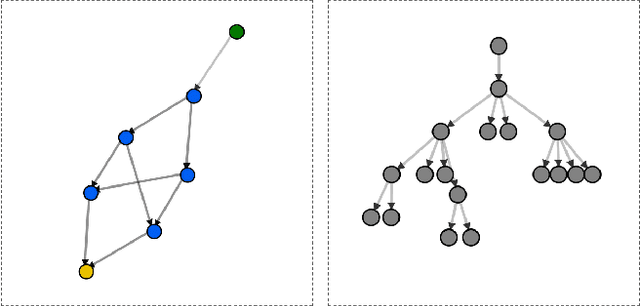
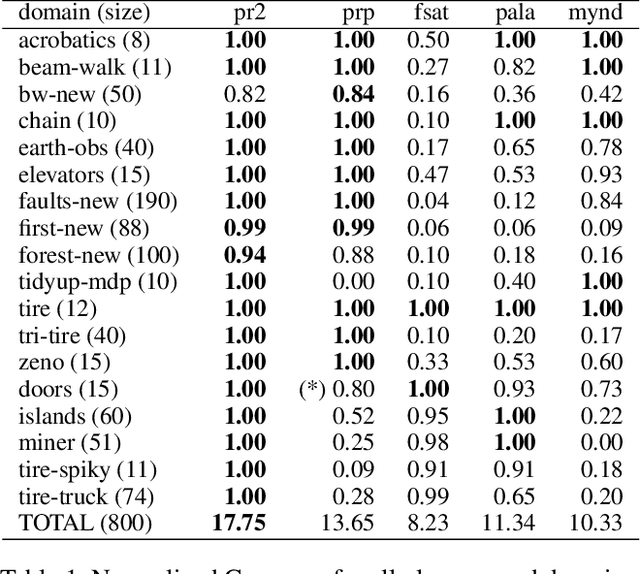
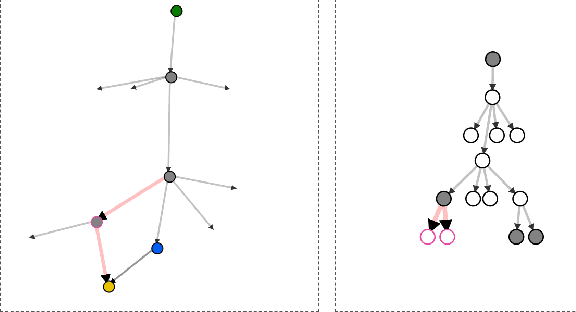
Fully Observable Non-Deterministic (FOND) planning is a variant of classical symbolic planning in which actions are nondeterministic, with an action's outcome known only upon execution. It is a popular planning paradigm with applications ranging from robot planning to dialogue-agent design and reactive synthesis. Over the last 20 years, a number of approaches to FOND planning have emerged. In this work, we establish a new state of the art, following in the footsteps of some of the most powerful FOND planners to date. Our planner, PR2, decisively outperforms the four leading FOND planners, at times by a large margin, in 17 of 18 domains that represent a comprehensive benchmark suite. Ablation studies demonstrate the impact of various techniques we introduce, with the largest improvement coming from our novel FOND-aware heuristic.

Domain-Independent Dynamic Programming: Generic State Space Search for Combinatorial Optimization

For combinatorial optimization problems, model-based approaches such as mixed-integer programming (MIP) and constraint programming (CP) aim to decouple modeling and solving a problem: the 'holy grail' of declarative problem solving. We propose domain-independent dynamic programming (DIDP), a new model-based paradigm based on dynamic programming (DP). While DP is not new, it has typically been implemented as a problem-specific method. We propose Dynamic Programming Description Language (DyPDL), a formalism to define DP models, and develop Cost-Algebraic A* Solver for DyPDL (CAASDy), a generic solver for DyPDL using state space search. We formalize existing problem-specific DP and state space search methods for combinatorial optimization problems as DP models in DyPDL. Using CAASDy and commercial MIP and CP solvers, we experimentally compare the DP models with existing MIP and CP models, showing that, despite its nascent nature, CAASDy outperforms MIP and CP on a number of common problem classes.

Comparing and Integrating Constraint Programming and Temporal Planning for Quantum Circuit Compilation

Recently, the makespan-minimization problem of compiling a general class of quantum algorithms into near-term quantum processors has been introduced to the AI community. The research demonstrated that temporal planning is a strong approach for a class of quantum circuit compilation (QCC) problems. In this paper, we explore the use of constraint programming (CP) as an alternative and complementary approach to temporal planning. We extend previous work by introducing two new problem variations that incorporate important characteristics identified by the quantum computing community. We apply temporal planning and CP to the baseline and extended QCC problems as both stand-alone and hybrid approaches. Our hybrid methods use solutions found by temporal planning to warm start CP, leveraging the ability of the former to find satisficing solutions to problems with a high degree of task optionality, an area that CP typically struggles with. The CP model, benefiting from inferred bounds on planning horizon length and task counts provided by the warm start, is then used to find higher quality solutions. Our empirical evaluation indicates that while stand-alone CP is only competitive for the smallest problems, CP in our hybridization with temporal planning out-performs stand-alone temporal planning in the majority of problem classes.

Scheduling a Dynamic Aircraft Repair Shop with Limited Repair Resources

We address a dynamic repair shop scheduling problem in the context of military aircraft fleet management where the goal is to maintain a full complement of aircraft over the long-term. A number of flights, each with a requirement for a specific number and type of aircraft, are already scheduled over a long horizon. We need to assign aircraft to flights and schedule repair activities while considering the flights requirements, repair capacity, and aircraft failures. The number of aircraft awaiting repair dynamically changes over time due to failures and it is therefore necessary to rebuild the repair schedule online. To solve the problem, we view the dynamic repair shop as successive static repair scheduling sub-problems over shorter time periods. We propose a complete approach based on the logic-based Benders decomposition to solve the static sub-problems, and design different rescheduling policies to schedule the dynamic repair shop. Computational experiments demonstrate that the Benders model is able to find and prove optimal solutions on average four times faster than a mixed integer programming model. The rescheduling approach having both aspects of scheduling over a longer horizon and quickly adjusting the schedule increases aircraft available in the long term by 10% compared to the approaches having either one of the aspects alone.

A Constraint Programming Approach for Solving a Queueing Control Problem

In a facility with front room and back room operations, it is useful to switch workers between the rooms in order to cope with changing customer demand. Assuming stochastic customer arrival and service times, we seek a policy for switching workers such that the expected customer waiting time is minimized while the expected back room staffing is sufficient to perform all work. Three novel constraint programming models and several shaving procedures for these models are presented. Experimental results show that a model based on closed-form expressions together with a combination of shaving procedures is the most efficient. This model is able to find and prove optimal solutions for many problem instances within a reasonable run-time. Previously, the only available approach was a heuristic algorithm. Furthermore, a hybrid method combining the heuristic and the best constraint programming method is shown to perform as well as the heuristic in terms of solution quality over time, while achieving the same performance in terms of proving optimality as the pure constraint programming model. This is the first work of which we are aware that solves such queueing-based problems with constraint programming.