Anomaly Detection in Aeronautics Data with Quantum-compatible Discrete Deep Generative Model

Deep generative learning cannot only be used for generating new data with statistical characteristics derived from input data but also for anomaly detection, by separating nominal and anomalous instances based on their reconstruction quality. In this paper, we explore the performance of three unsupervised deep generative models -- variational autoencoders (VAEs) with Gaussian, Bernoulli, and Boltzmann priors -- in detecting anomalies in flight-operations data of commercial flights consisting of multivariate time series. We devised two VAE models with discrete latent variables (DVAEs), one with a factorized Bernoulli prior and one with a restricted Boltzmann machine (RBM) as prior, because of the demand for discrete-variable models in machine-learning applications and because the integration of quantum devices based on two-level quantum systems requires such models. The DVAE with RBM prior, using a relatively simple -- and classically or quantum-mechanically enhanceable -- sampling technique for the evolution of the RBM's negative phase, performed better than the Bernoulli DVAE and on par with the Gaussian model, which has a continuous latent space. Our studies demonstrate the competitiveness of a discrete deep generative model with its Gaussian counterpart on anomaly-detection tasks. Moreover, the DVAE model with RBM prior can be easily integrated with quantum sampling by outsourcing its generative process to measurements of quantum states obtained from a quantum annealer or gate-model device.

High-Dimensional Similarity Search with Quantum-Assisted Variational Autoencoder

Recent progress in quantum algorithms and hardware indicates the potential importance of quantum computing in the near future. However, finding suitable application areas remains an active area of research. Quantum machine learning is touted as a potential approach to demonstrate quantum advantage within both the gate-model and the adiabatic schemes. For instance, the Quantum-assisted Variational Autoencoder has been proposed as a quantum enhancement to the discrete VAE. We extend on previous work and study the real-world applicability of a QVAE by presenting a proof-of-concept for similarity search in large-scale high-dimensional datasets. While exact and fast similarity search algorithms are available for low dimensional datasets, scaling to high-dimensional data is non-trivial. We show how to construct a space-efficient search index based on the latent space representation of a QVAE. Our experiments show a correlation between the Hamming distance in the embedded space and the Euclidean distance in the original space on the Moderate Resolution Imaging Spectroradiometer (MODIS) dataset. Further, we find real-world speedups compared to linear search and demonstrate memory-efficient scaling to half a billion data points.

Planning for Compilation of a Quantum Algorithm for Graph Coloring

The problem of compiling general quantum algorithms for implementation on near-term quantum processors has been introduced to the AI community. Previous work demonstrated that temporal planning is an attractive approach for part of this compilationtask, specifically, the routing of circuits that implement the Quantum Alternating Operator Ansatz (QAOA) applied to the MaxCut problem on a quantum processor architecture. In this paper, we extend the earlier work to route circuits that implement QAOA for Graph Coloring problems. QAOA for coloring requires execution of more, and more complex, operations on the chip, which makes routing a more challenging problem. We evaluate the approach on state-of-the-art hardware architectures from leading quantum computing companies. Additionally, we apply a planning approach to qubit initialization. Our empirical evaluation shows that temporal planning compares well to reasonable analytic upper bounds, and that solving qubit initialization with a classical planner generally helps temporal planners in finding shorter-makespan compilations for QAOA for Graph Coloring. These advances suggest that temporal planning can be an effective approach for more complex quantum computing algorithms and architectures.

Optimizing quantum heuristics with meta-learning

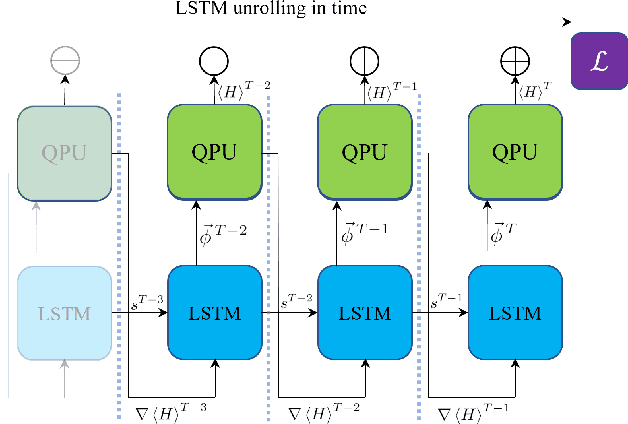
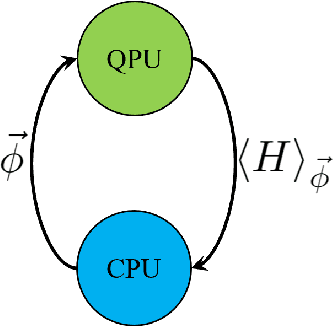
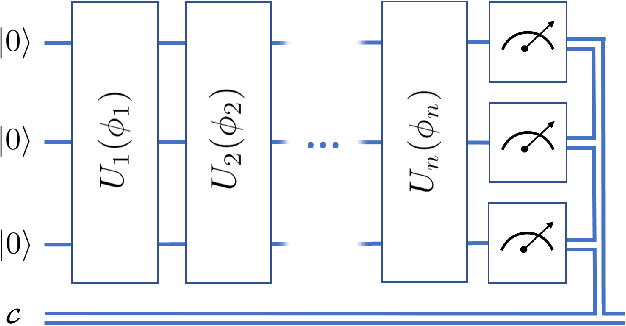
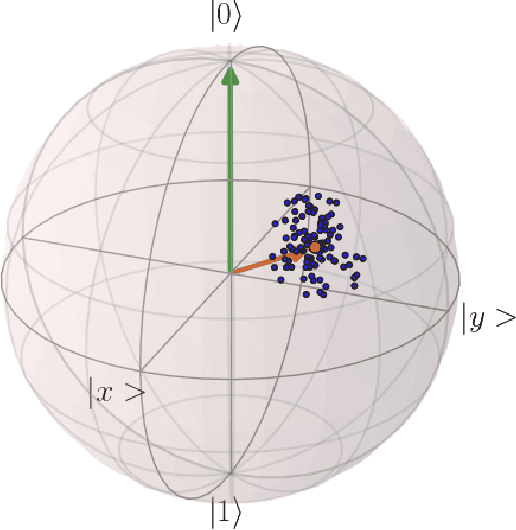
Variational quantum algorithms, a class of quantum heuristics, are promising candidates for the demonstration of useful quantum computation. Finding the best way to amplify the performance of these methods on hardware is an important task. Here, we evaluate the optimization of quantum heuristics with an existing class of techniques called `meta-learners'. We compare the performance of a meta-learner to Bayesian optimization, evolutionary strategies, L-BFGS-B and Nelder-Mead approaches, for two quantum heuristics (quantum alternating operator ansatz and variational quantum eigensolver), on three problems, in three simulation environments. We show that the meta-learner comes near to the global optima more frequently than all other optimizers we tested in a noisy parameter setting environment. We also find that the meta-learner is generally more resistant to noise, for example seeing a smaller reduction in performance in Noisy and Sampling environments and performs better on average by a `gain' metric than its closest comparable competitor L-BFGS-B. These results are an important indication that meta-learning and associated machine learning methods will be integral to the useful application of noisy near-term quantum computers.

Quantum-assisted associative adversarial network: Applying quantum annealing in deep learning

We present an algorithm for learning a latent variable generative model via generative adversarial learning where the canonical uniform noise input is replaced by samples from a graphical model. This graphical model is learned by a Boltzmann machine which learns low-dimensional feature representation of data extracted by the discriminator. A quantum annealer, the D-Wave 2000Q, is used to sample from this model. This algorithm joins a growing family of algorithms that use a quantum annealing subroutine in deep learning, and provides a framework to test the advantages of quantum-assisted learning in GANs. Fully connected, symmetric bipartite and Chimera graph topologies are compared on a reduced stochastically binarized MNIST dataset, for both classical and quantum annealing sampling methods. The quantum-assisted associative adversarial network successfully learns a generative model of the MNIST dataset for all topologies, and is also applied to the LSUN dataset bedrooms class for the Chimera topology. Evaluated using the Fr\'{e}chet inception distance and inception score, the quantum and classical versions of the algorithm are found to have equivalent performance for learning an implicit generative model of the MNIST dataset.

Comparing and Integrating Constraint Programming and Temporal Planning for Quantum Circuit Compilation

Recently, the makespan-minimization problem of compiling a general class of quantum algorithms into near-term quantum processors has been introduced to the AI community. The research demonstrated that temporal planning is a strong approach for a class of quantum circuit compilation (QCC) problems. In this paper, we explore the use of constraint programming (CP) as an alternative and complementary approach to temporal planning. We extend previous work by introducing two new problem variations that incorporate important characteristics identified by the quantum computing community. We apply temporal planning and CP to the baseline and extended QCC problems as both stand-alone and hybrid approaches. Our hybrid methods use solutions found by temporal planning to warm start CP, leveraging the ability of the former to find satisficing solutions to problems with a high degree of task optionality, an area that CP typically struggles with. The CP model, benefiting from inferred bounds on planning horizon length and task counts provided by the warm start, is then used to find higher quality solutions. Our empirical evaluation indicates that while stand-alone CP is only competitive for the smallest problems, CP in our hybridization with temporal planning out-performs stand-alone temporal planning in the majority of problem classes.

Compiling quantum circuits to realistic hardware architectures using temporal planners

To run quantum algorithms on emerging gate-model quantum hardware, quantum circuits must be compiled to take into account constraints on the hardware. For near-term hardware, with only limited means to mitigate decoherence, it is critical to minimize the duration of the circuit. We investigate the application of temporal planners to the problem of compiling quantum circuits to newly emerging quantum hardware. While our approach is general, we focus on compiling to superconducting hardware architectures with nearest neighbor constraints. Our initial experiments focus on compiling Quantum Alternating Operator Ansatz (QAOA) circuits whose high number of commuting gates allow great flexibility in the order in which the gates can be applied. That freedom makes it more challenging to find optimal compilations but also means there is a greater potential win from more optimized compilation than for less flexible circuits. We map this quantum circuit compilation problem to a temporal planning problem, and generated a test suite of compilation problems for QAOA circuits of various sizes to a realistic hardware architecture. We report compilation results from several state-of-the-art temporal planners on this test set. This early empirical evaluation demonstrates that temporal planning is a viable approach to quantum circuit compilation.