High-Dimensional Similarity Search with Quantum-Assisted Variational Autoencoder

Recent progress in quantum algorithms and hardware indicates the potential importance of quantum computing in the near future. However, finding suitable application areas remains an active area of research. Quantum machine learning is touted as a potential approach to demonstrate quantum advantage within both the gate-model and the adiabatic schemes. For instance, the Quantum-assisted Variational Autoencoder has been proposed as a quantum enhancement to the discrete VAE. We extend on previous work and study the real-world applicability of a QVAE by presenting a proof-of-concept for similarity search in large-scale high-dimensional datasets. While exact and fast similarity search algorithms are available for low dimensional datasets, scaling to high-dimensional data is non-trivial. We show how to construct a space-efficient search index based on the latent space representation of a QVAE. Our experiments show a correlation between the Hamming distance in the embedded space and the Euclidean distance in the original space on the Moderate Resolution Imaging Spectroradiometer (MODIS) dataset. Further, we find real-world speedups compared to linear search and demonstrate memory-efficient scaling to half a billion data points.

Optimizing quantum heuristics with meta-learning

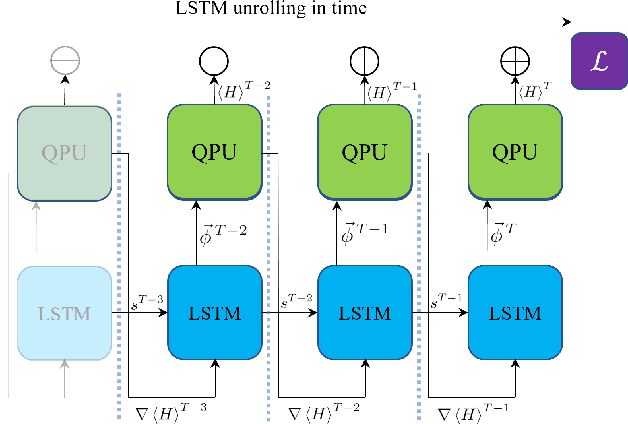
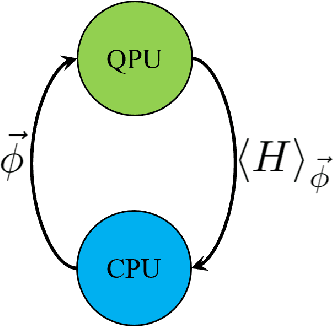
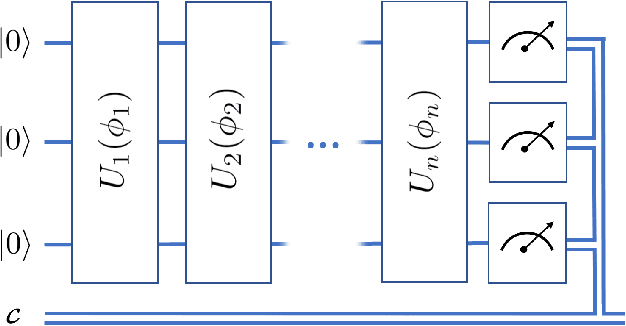
Variational quantum algorithms, a class of quantum heuristics, are promising candidates for the demonstration of useful quantum computation. Finding the best way to amplify the performance of these methods on hardware is an important task. Here, we evaluate the optimization of quantum heuristics with an existing class of techniques called `meta-learners'. We compare the performance of a meta-learner to Bayesian optimization, evolutionary strategies, L-BFGS-B and Nelder-Mead approaches, for two quantum heuristics (quantum alternating operator ansatz and variational quantum eigensolver), on three problems, in three simulation environments. We show that the meta-learner comes near to the global optima more frequently than all other optimizers we tested in a noisy parameter setting environment. We also find that the meta-learner is generally more resistant to noise, for example seeing a smaller reduction in performance in Noisy and Sampling environments and performs better on average by a `gain' metric than its closest comparable competitor L-BFGS-B. These results are an important indication that meta-learning and associated machine learning methods will be integral to the useful application of noisy near-term quantum computers.

Quantum-assisted associative adversarial network: Applying quantum annealing in deep learning

We present an algorithm for learning a latent variable generative model via generative adversarial learning where the canonical uniform noise input is replaced by samples from a graphical model. This graphical model is learned by a Boltzmann machine which learns low-dimensional feature representation of data extracted by the discriminator. A quantum annealer, the D-Wave 2000Q, is used to sample from this model. This algorithm joins a growing family of algorithms that use a quantum annealing subroutine in deep learning, and provides a framework to test the advantages of quantum-assisted learning in GANs. Fully connected, symmetric bipartite and Chimera graph topologies are compared on a reduced stochastically binarized MNIST dataset, for both classical and quantum annealing sampling methods. The quantum-assisted associative adversarial network successfully learns a generative model of the MNIST dataset for all topologies, and is also applied to the LSUN dataset bedrooms class for the Chimera topology. Evaluated using the Fr\'{e}chet inception distance and inception score, the quantum and classical versions of the algorithm are found to have equivalent performance for learning an implicit generative model of the MNIST dataset.