Classical symmetries and QAOA

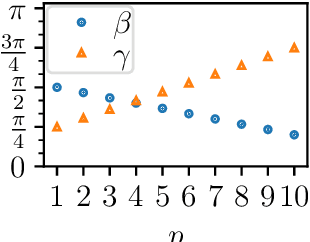
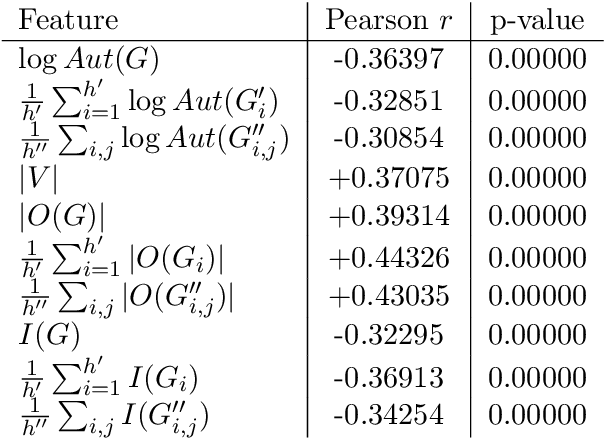
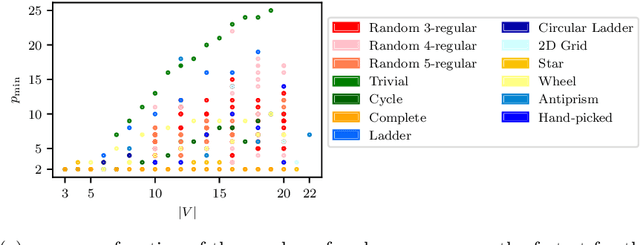
We study the relationship between the Quantum Approximate Optimization Algorithm (QAOA) and the underlying symmetries of the objective function to be optimized. Our approach formalizes the connection between quantum symmetry properties of the QAOA dynamics and the group of classical symmetries of the objective function. The connection is general and includes but is not limited to problems defined on graphs. We show a series of results exploring the connection and highlight examples of hard problem classes where a nontrivial symmetry subgroup can be obtained efficiently. In particular we show how classical objective function symmetries lead to invariant measurement outcome probabilities across states connected by such symmetries, independent of the choice of algorithm parameters or number of layers. To illustrate the power of the developed connection, we apply machine learning techniques towards predicting QAOA performance based on symmetry considerations. We provide numerical evidence that a small set of graph symmetry properties suffices to predict the minimum QAOA depth required to achieve a target approximation ratio on the MaxCut problem, in a practically important setting where QAOA parameter schedules are constrained to be linear and hence easier to optimize.

Optimizing quantum heuristics with meta-learning

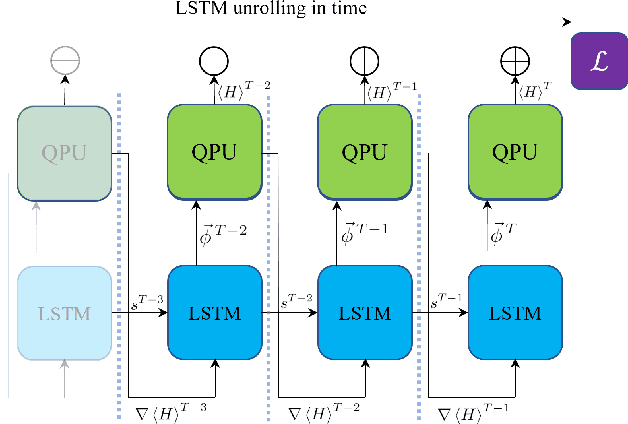
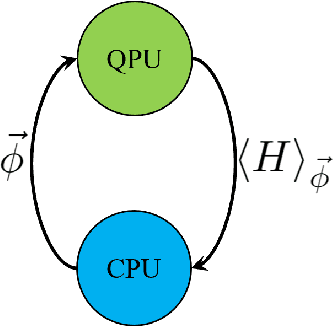
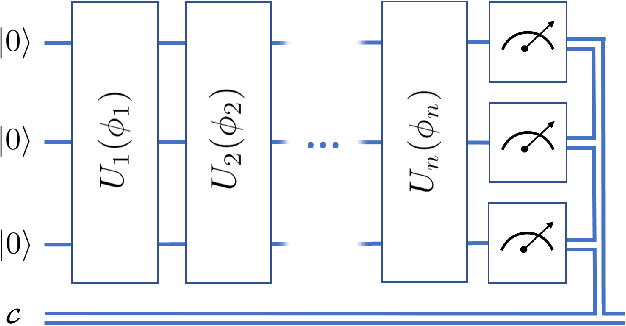
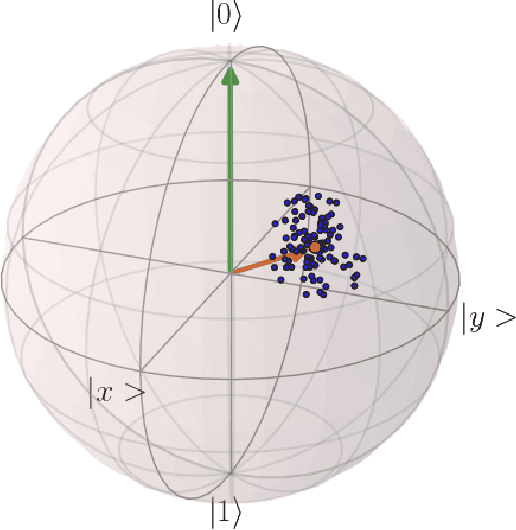
Variational quantum algorithms, a class of quantum heuristics, are promising candidates for the demonstration of useful quantum computation. Finding the best way to amplify the performance of these methods on hardware is an important task. Here, we evaluate the optimization of quantum heuristics with an existing class of techniques called `meta-learners'. We compare the performance of a meta-learner to Bayesian optimization, evolutionary strategies, L-BFGS-B and Nelder-Mead approaches, for two quantum heuristics (quantum alternating operator ansatz and variational quantum eigensolver), on three problems, in three simulation environments. We show that the meta-learner comes near to the global optima more frequently than all other optimizers we tested in a noisy parameter setting environment. We also find that the meta-learner is generally more resistant to noise, for example seeing a smaller reduction in performance in Noisy and Sampling environments and performs better on average by a `gain' metric than its closest comparable competitor L-BFGS-B. These results are an important indication that meta-learning and associated machine learning methods will be integral to the useful application of noisy near-term quantum computers.