Matrix Tile Analysis
Paper and Code
Jun 27, 2012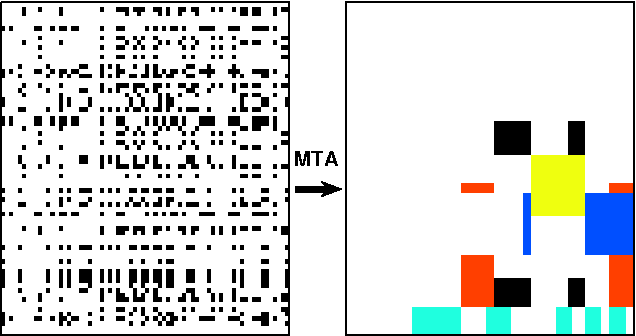
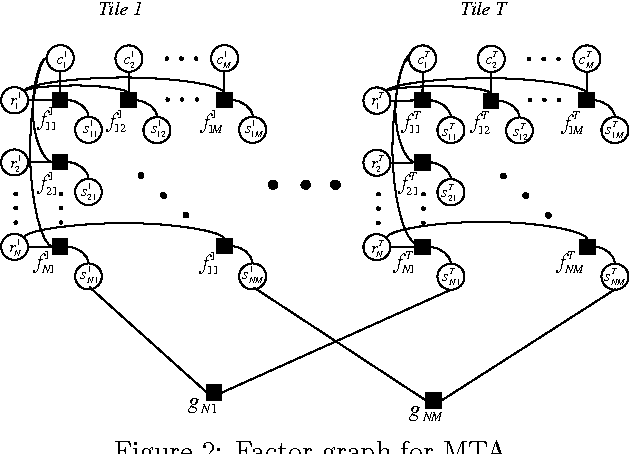
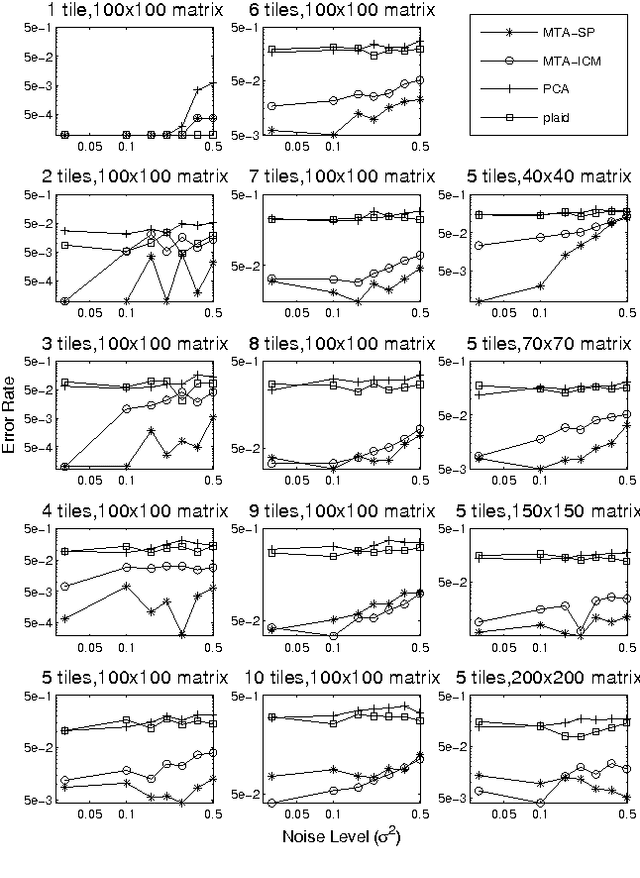

Many tasks require finding groups of elements in a matrix of numbers, symbols or class likelihoods. One approach is to use efficient bi- or tri-linear factorization techniques including PCA, ICA, sparse matrix factorization and plaid analysis. These techniques are not appropriate when addition and multiplication of matrix elements are not sensibly defined. More directly, methods like bi-clustering can be used to classify matrix elements, but these methods make the overly-restrictive assumption that the class of each element is a function of a row class and a column class. We introduce a general computational problem, `matrix tile analysis' (MTA), which consists of decomposing a matrix into a set of non-overlapping tiles, each of which is defined by a subset of usually nonadjacent rows and columns. MTA does not require an algebra for combining tiles, but must search over discrete combinations of tile assignments. Exact MTA is a computationally intractable integer programming problem, but we describe an approximate iterative technique and a computationally efficient sum-product relaxation of the integer program. We compare the effectiveness of these methods to PCA and plaid on hundreds of randomly generated tasks. Using double-gene-knockout data, we show that MTA finds groups of interacting yeast genes that have biologically-related functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge