Matrix Tile Analysis

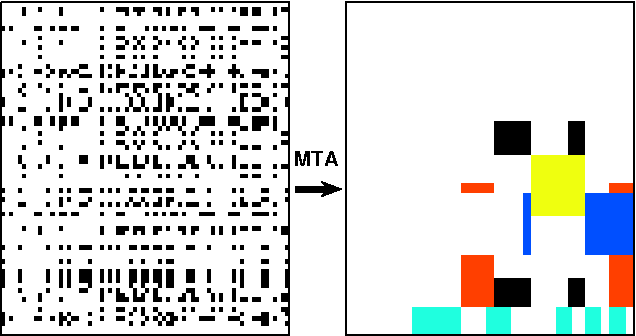
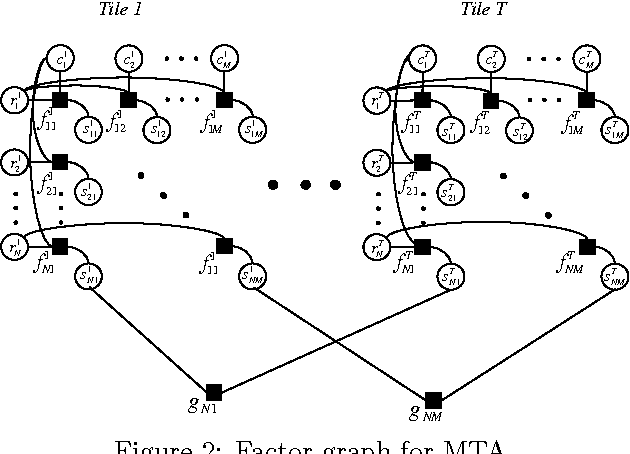
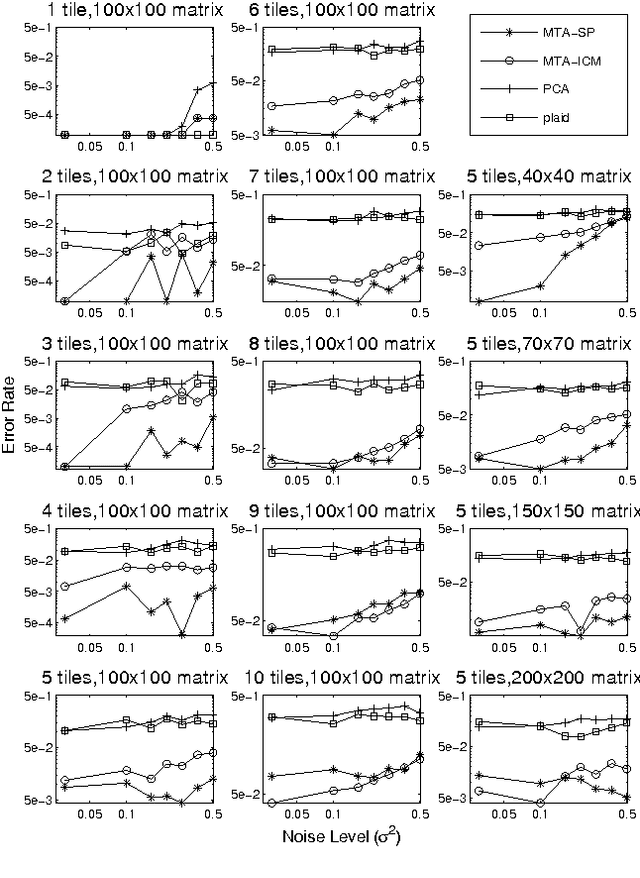
Many tasks require finding groups of elements in a matrix of numbers, symbols or class likelihoods. One approach is to use efficient bi- or tri-linear factorization techniques including PCA, ICA, sparse matrix factorization and plaid analysis. These techniques are not appropriate when addition and multiplication of matrix elements are not sensibly defined. More directly, methods like bi-clustering can be used to classify matrix elements, but these methods make the overly-restrictive assumption that the class of each element is a function of a row class and a column class. We introduce a general computational problem, `matrix tile analysis' (MTA), which consists of decomposing a matrix into a set of non-overlapping tiles, each of which is defined by a subset of usually nonadjacent rows and columns. MTA does not require an algebra for combining tiles, but must search over discrete combinations of tile assignments. Exact MTA is a computationally intractable integer programming problem, but we describe an approximate iterative technique and a computationally efficient sum-product relaxation of the integer program. We compare the effectiveness of these methods to PCA and plaid on hundreds of randomly generated tasks. Using double-gene-knockout data, we show that MTA finds groups of interacting yeast genes that have biologically-related functions.

Hierarchical Affinity Propagation

Affinity propagation is an exemplar-based clustering algorithm that finds a set of data-points that best exemplify the data, and associates each datapoint with one exemplar. We extend affinity propagation in a principled way to solve the hierarchical clustering problem, which arises in a variety of domains including biology, sensor networks and decision making in operational research. We derive an inference algorithm that operates by propagating information up and down the hierarchy, and is efficient despite the high-order potentials required for the graphical model formulation. We demonstrate that our method outperforms greedy techniques that cluster one layer at a time. We show that on an artificial dataset designed to mimic the HIV-strain mutation dynamics, our method outperforms related methods. For real HIV sequences, where the ground truth is not available, we show our method achieves better results, in terms of the underlying objective function, and show the results correspond meaningfully to geographical location and strain subtypes. Finally we report results on using the method for the analysis of mass spectra, showing it performs favorably compared to state-of-the-art methods.