From Interpretation to Correction: A Decentralized Optimization Framework for Exact Convergence in Federated Learning

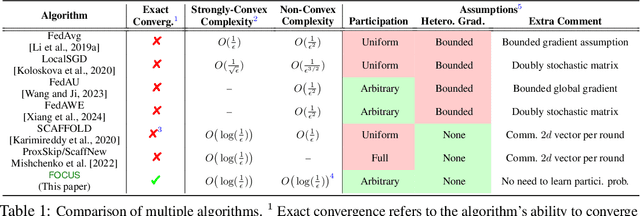
This work introduces a novel decentralized framework to interpret federated learning (FL) and, consequently, correct the biases introduced by arbitrary client participation and data heterogeneity, which are two typical traits in practical FL. Specifically, we first reformulate the core processes of FedAvg - client participation, local updating, and model aggregation - as stochastic matrix multiplications. This reformulation allows us to interpret FedAvg as a decentralized algorithm. Leveraging the decentralized optimization framework, we are able to provide a concise analysis to quantify the impact of arbitrary client participation and data heterogeneity on FedAvg's convergence point. This insight motivates the development of Federated Optimization with Exact Convergence via Push-pull Strategy (FOCUS), a novel algorithm inspired by the decentralized algorithm that eliminates these biases and achieves exact convergence without requiring the bounded heterogeneity assumption. Furthermore, we theoretically prove that FOCUS exhibits linear convergence (exponential decay) for both strongly convex and non-convex functions satisfying the Polyak-Lojasiewicz condition, regardless of the arbitrary nature of client participation.

Achieving Dimension-Free Communication in Federated Learning via Zeroth-Order Optimization

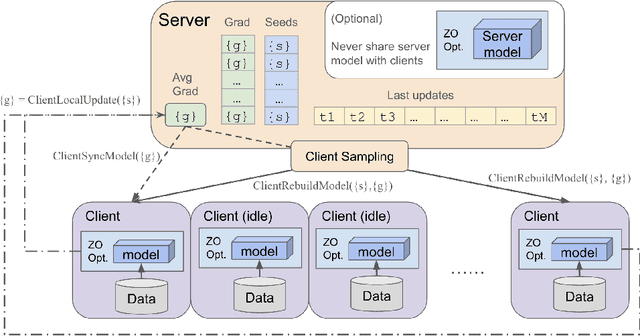
Federated Learning (FL) offers a promising framework for collaborative and privacy-preserving machine learning across distributed data sources. However, the substantial communication costs associated with FL pose a significant challenge to its efficiency. Specifically, in each communication round, the communication costs scale linearly with the model's dimension, which presents a formidable obstacle, especially in large model scenarios. Despite various communication efficient strategies, the intrinsic dimension-dependent communication cost remains a major bottleneck for current FL implementations. In this paper, we introduce a novel dimension-free communication strategy for FL, leveraging zero-order optimization techniques. We propose a new algorithm, FedDisco, which facilitates the transmission of only a constant number of scalar values between clients and the server in each communication round, thereby reducing the communication cost from $\mathscr{O}(d)$ to $\mathscr{O}(1)$, where $d$ is the dimension of the model parameters. Theoretically, in non-convex functions, we prove that our algorithm achieves state-of-the-art rates, which show a linear speedup of the number of clients and local steps under standard assumptions and dimension-free rate for low effective rank scenarios. Empirical evaluations through classic deep learning training and large language model fine-tuning substantiate significant reductions in communication overhead compared to traditional FL approaches.

DSGD-CECA: Decentralized SGD with Communication-Optimal Exact Consensus Algorithm

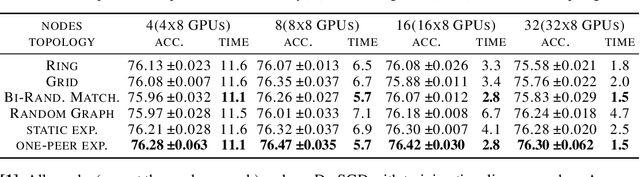
Decentralized Stochastic Gradient Descent (SGD) is an emerging neural network training approach that enables multiple agents to train a model collaboratively and simultaneously. Rather than using a central parameter server to collect gradients from all the agents, each agent keeps a copy of the model parameters and communicates with a small number of other agents to exchange model updates. Their communication, governed by the communication topology and gossip weight matrices, facilitates the exchange of model updates. The state-of-the-art approach uses the dynamic one-peer exponential-2 topology, achieving faster training times and improved scalability than the ring, grid, torus, and hypercube topologies. However, this approach requires a power-of-2 number of agents, which is impractical at scale. In this paper, we remove this restriction and propose \underline{D}ecentralized \underline{SGD} with \underline{C}ommunication-optimal \underline{E}xact \underline{C}onsensus \underline{A}lgorithm (DSGD-CECA), which works for any number of agents while still achieving state-of-the-art properties. In particular, DSGD-CECA incurs a unit per-iteration communication overhead and an $\tilde{O}(n^3)$ transient iteration complexity. Our proof is based on newly discovered properties of gossip weight matrices and a novel approach to combine them with DSGD's convergence analysis. Numerical experiments show the efficiency of DSGD-CECA.

BlueFog: Make Decentralized Algorithms Practical for Optimization and Deep Learning

Decentralized algorithm is a form of computation that achieves a global goal through local dynamics that relies on low-cost communication between directly-connected agents. On large-scale optimization tasks involving distributed datasets, decentralized algorithms have shown strong, sometimes superior, performance over distributed algorithms with a central node. Recently, developing decentralized algorithms for deep learning has attracted great attention. They are considered as low-communication-overhead alternatives to those using a parameter server or the Ring-Allreduce protocol. However, the lack of an easy-to-use and efficient software package has kept most decentralized algorithms merely on paper. To fill the gap, we introduce BlueFog, a python library for straightforward, high-performance implementations of diverse decentralized algorithms. Based on a unified abstraction of various communication operations, BlueFog offers intuitive interfaces to implement a spectrum of decentralized algorithms, from those using a static, undirected graph for synchronous operations to those using dynamic and directed graphs for asynchronous operations. BlueFog also adopts several system-level acceleration techniques to further optimize the performance on the deep learning tasks. On mainstream DNN training tasks, BlueFog reaches a much higher throughput and achieves an overall $1.2\times \sim 1.8\times$ speedup over Horovod, a state-of-the-art distributed deep learning package based on Ring-Allreduce. BlueFog is open source at https://github.com/Bluefog-Lib/bluefog.

Exponential Graph is Provably Efficient for Decentralized Deep Training

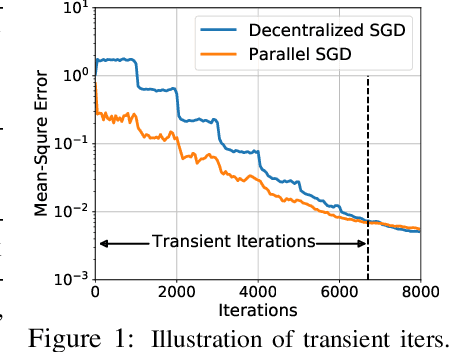
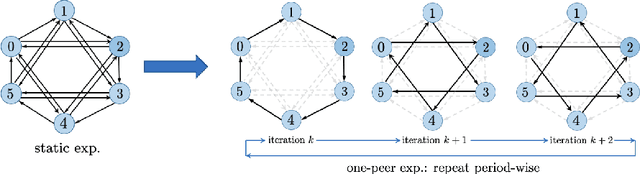
Decentralized SGD is an emerging training method for deep learning known for its much less (thus faster) communication per iteration, which relaxes the averaging step in parallel SGD to inexact averaging. The less exact the averaging is, however, the more the total iterations the training needs to take. Therefore, the key to making decentralized SGD efficient is to realize nearly-exact averaging using little communication. This requires a skillful choice of communication topology, which is an under-studied topic in decentralized optimization. In this paper, we study so-called exponential graphs where every node is connected to $O(\log(n))$ neighbors and $n$ is the total number of nodes. This work proves such graphs can lead to both fast communication and effective averaging simultaneously. We also discover that a sequence of $\log(n)$ one-peer exponential graphs, in which each node communicates to one single neighbor per iteration, can together achieve exact averaging. This favorable property enables one-peer exponential graph to average as effective as its static counterpart but communicates more efficiently. We apply these exponential graphs in decentralized (momentum) SGD to obtain the state-of-the-art balance between per-iteration communication and iteration complexity among all commonly-used topologies. Experimental results on a variety of tasks and models demonstrate that decentralized (momentum) SGD over exponential graphs promises both fast and high-quality training. Our code is implemented through BlueFog and available at https://github.com/Bluefog-Lib/NeurIPS2021-Exponential-Graph.

On the Performance of Exact Diffusion over Adaptive Networks

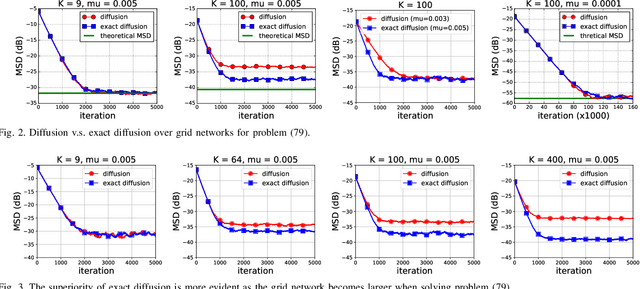
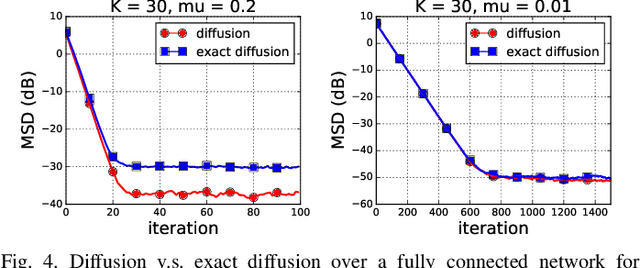
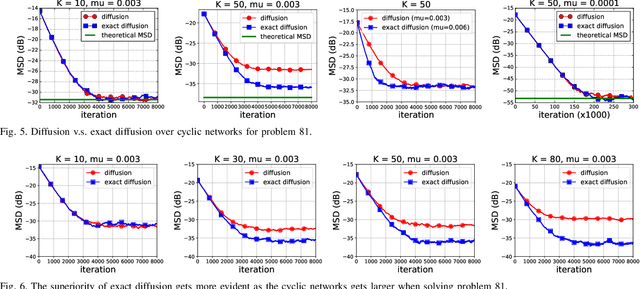
Various bias-correction methods such as EXTRA, DIGing, and exact diffusion have been proposed recently to solve distributed deterministic optimization problems. These methods employ constant step-sizes and converge linearly to the {\em exact} solution under proper conditions. However, their performance under stochastic and adaptive settings remains unclear. It is still unknown whether the bias-correction is necessary over adaptive networks. By studying exact diffusion and examining its steady-state performance under stochastic scenarios, this paper provides affirmative results. It is shown that the correction step in exact diffusion leads to better steady-state performance than traditional methods. It is also analytically shown the superiority of exact diffusion is more evident over badly-connected network topologies.

Stochastic Learning under Random Reshuffling with Constant Step-sizes

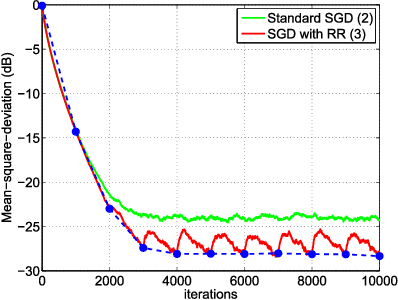
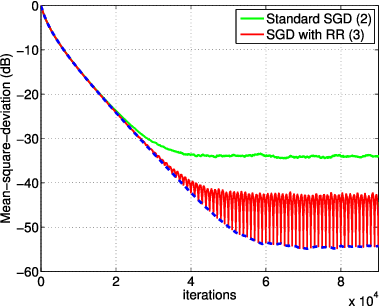
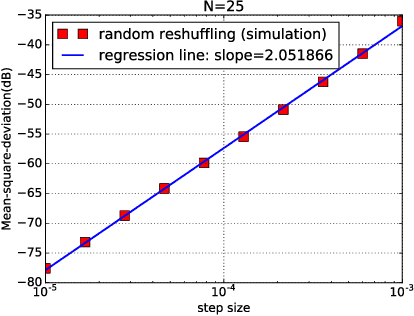
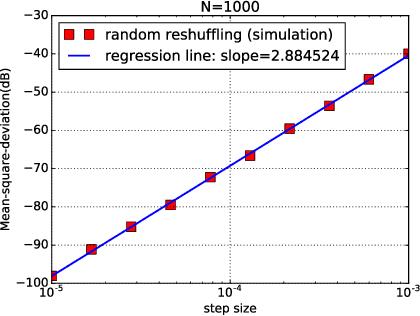
In empirical risk optimization, it has been observed that stochastic gradient implementations that rely on random reshuffling of the data achieve better performance than implementations that rely on sampling the data uniformly. Recent works have pursued justifications for this behavior by examining the convergence rate of the learning process under diminishing step-sizes. This work focuses on the constant step-size case and strongly convex loss function. In this case, convergence is guaranteed to a small neighborhood of the optimizer albeit at a linear rate. The analysis establishes analytically that random reshuffling outperforms uniform sampling by showing explicitly that iterates approach a smaller neighborhood of size $O(\mu^2)$ around the minimizer rather than $O(\mu)$. Furthermore, we derive an analytical expression for the steady-state mean-square-error performance of the algorithm, which helps clarify in greater detail the differences between sampling with and without replacement. We also explain the periodic behavior that is observed in random reshuffling implementations.

Variance-Reduced Stochastic Learning by Networked Agents under Random Reshuffling

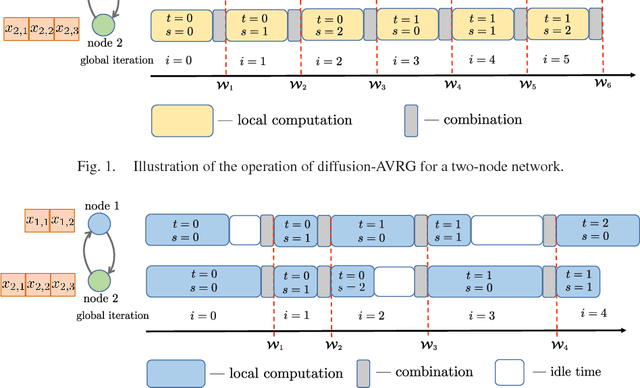
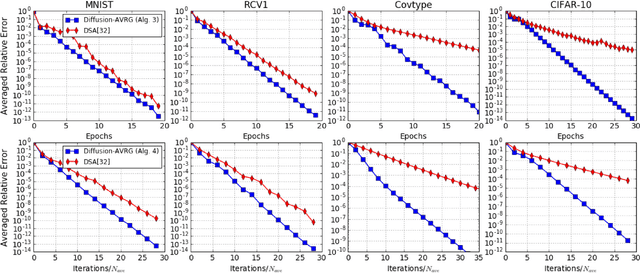
A new amortized variance-reduced gradient (AVRG) algorithm was developed in \cite{ying2017convergence}, which has constant storage requirement in comparison to SAGA and balanced gradient computations in comparison to SVRG. One key advantage of the AVRG strategy is its amenability to decentralized implementations. In this work, we show how AVRG can be extended to the network case where multiple learning agents are assumed to be connected by a graph topology. In this scenario, each agent observes data that is spatially distributed and all agents are only allowed to communicate with direct neighbors. Moreover, the amount of data observed by the individual agents may differ drastically. For such situations, the balanced gradient computation property of AVRG becomes a real advantage in reducing idle time caused by unbalanced local data storage requirements, which is characteristic of other reduced-variance gradient algorithms. The resulting diffusion-AVRG algorithm is shown to have linear convergence to the exact solution, and is much more memory efficient than other alternative algorithms. In addition, we propose a mini-batch strategy to balance the communication and computation efficiency for diffusion-AVRG. When a proper batch size is employed, it is observed in simulations that diffusion-AVRG is more computationally efficient than exact diffusion or EXTRA while maintaining almost the same communication efficiency.

Learning Under Distributed Features

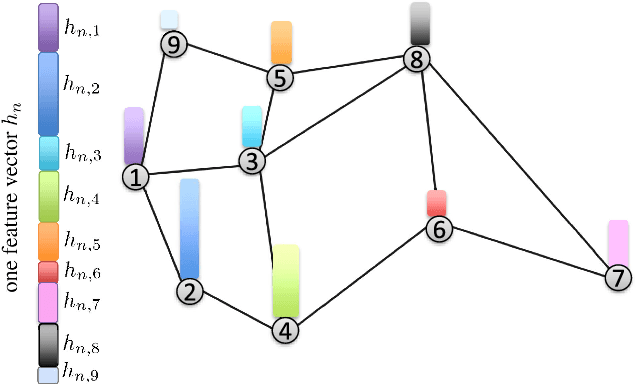
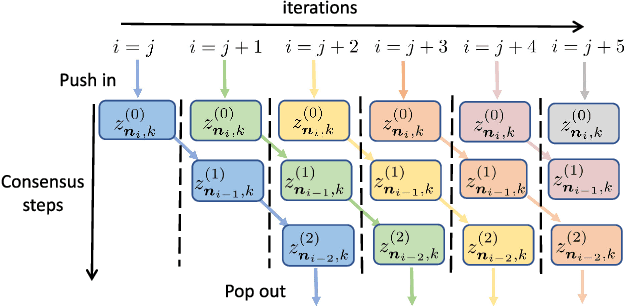
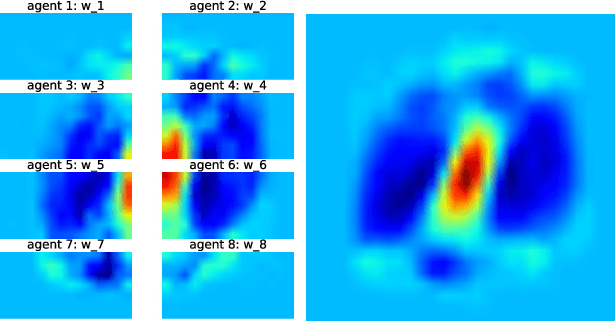
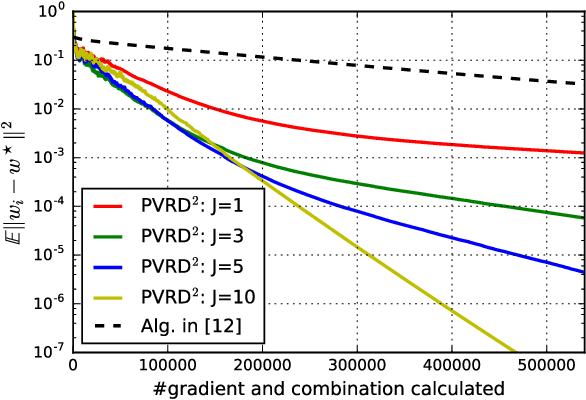
This work studies the problem of learning under both large data and large feature space scenarios. The feature information is assumed to be spread across agents in a network, where each agent observes some of the features. Through local cooperation, the agents are supposed to interact with each other to solve the inference problem and converge towards the global minimizer of the empirical risk. We study this problem exclusively in the primal domain, and propose new and effective distributed solutions with guaranteed convergence to the minimizer. This is achieved by combining a dynamic diffusion construction, a pipeline strategy, and variance-reduced techniques. Simulation results illustrate the conclusions.

Variance-Reduced Stochastic Learning under Random Reshuffling

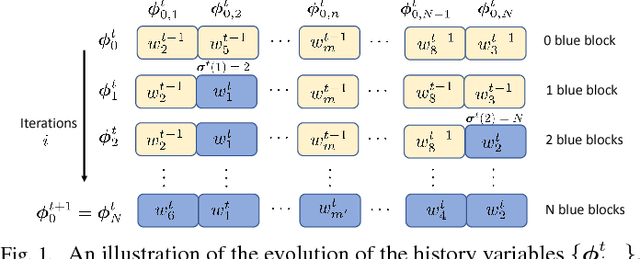
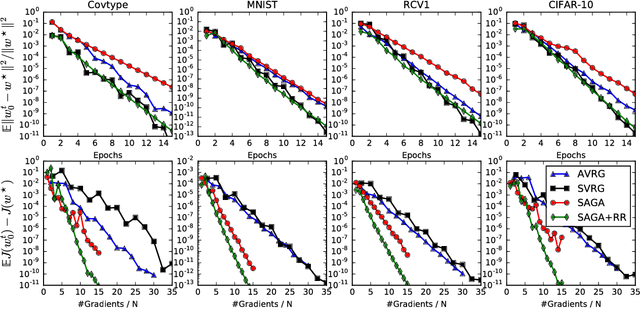
Several useful variance-reduced stochastic gradient algorithms, such as SVRG, SAGA, Finito, and SAG, have been proposed to minimize empirical risks with linear convergence properties to the exact minimizer. The existing convergence results assume uniform data sampling with replacement. However, it has been observed in related works that random reshuffling can deliver superior performance over uniform sampling and, yet, no formal proofs or guarantees of exact convergence exist for variance-reduced algorithms under random reshuffling. This paper makes two contributions. First, it resolves this open issue and provides the first theoretical guarantee of linear convergence under random reshuffling for SAGA; the argument is also adaptable to other variance-reduced algorithms. Second, under random reshuffling, the paper proposes a new amortized variance-reduced gradient (AVRG) algorithm with constant storage requirements compared to SAGA and with balanced gradient computations compared to SVRG. AVRG is also shown analytically to converge linearly.