Learning Under Distributed Features

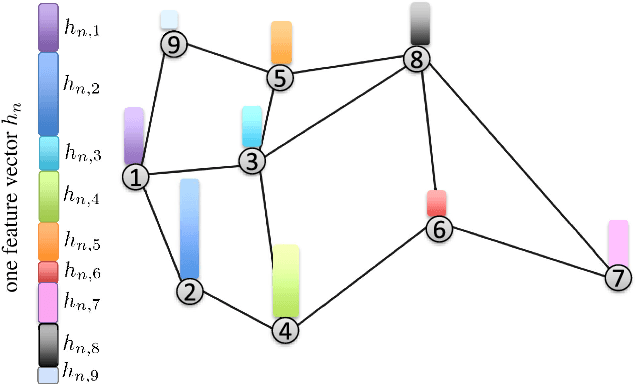
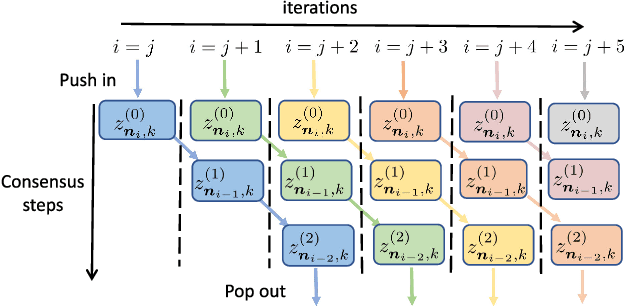
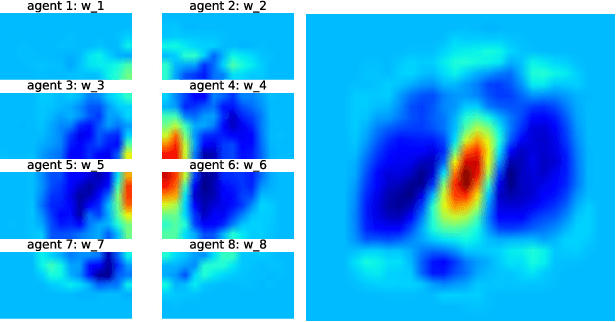
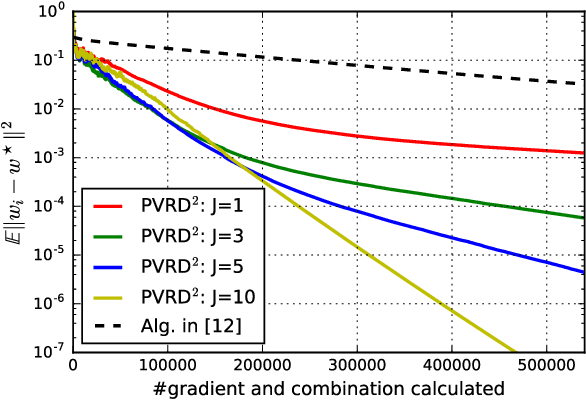
This work studies the problem of learning under both large data and large feature space scenarios. The feature information is assumed to be spread across agents in a network, where each agent observes some of the features. Through local cooperation, the agents are supposed to interact with each other to solve the inference problem and converge towards the global minimizer of the empirical risk. We study this problem exclusively in the primal domain, and propose new and effective distributed solutions with guaranteed convergence to the minimizer. This is achieved by combining a dynamic diffusion construction, a pipeline strategy, and variance-reduced techniques. Simulation results illustrate the conclusions.