Stochastic Learning under Random Reshuffling with Constant Step-sizes
Paper and Code
Oct 09, 2018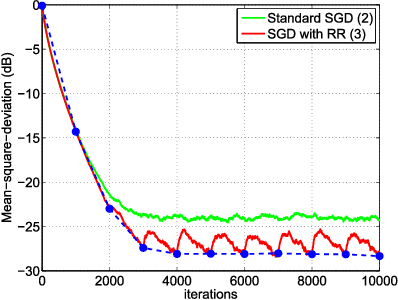
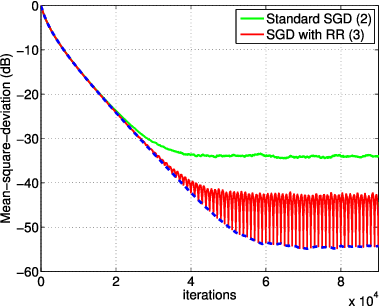
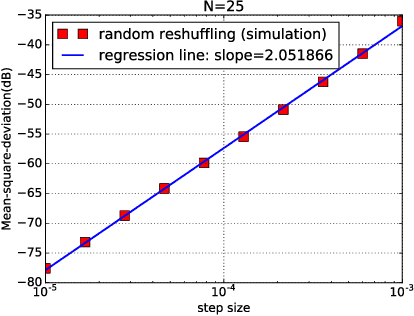
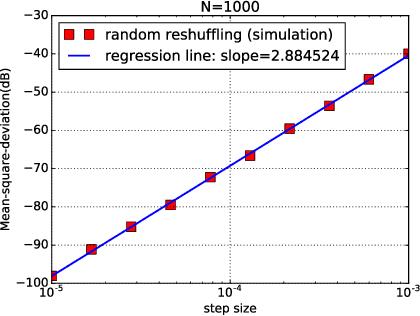
In empirical risk optimization, it has been observed that stochastic gradient implementations that rely on random reshuffling of the data achieve better performance than implementations that rely on sampling the data uniformly. Recent works have pursued justifications for this behavior by examining the convergence rate of the learning process under diminishing step-sizes. This work focuses on the constant step-size case and strongly convex loss function. In this case, convergence is guaranteed to a small neighborhood of the optimizer albeit at a linear rate. The analysis establishes analytically that random reshuffling outperforms uniform sampling by showing explicitly that iterates approach a smaller neighborhood of size $O(\mu^2)$ around the minimizer rather than $O(\mu)$. Furthermore, we derive an analytical expression for the steady-state mean-square-error performance of the algorithm, which helps clarify in greater detail the differences between sampling with and without replacement. We also explain the periodic behavior that is observed in random reshuffling implementations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge