On the Performance of Exact Diffusion over Adaptive Networks
Paper and Code
Mar 26, 2019
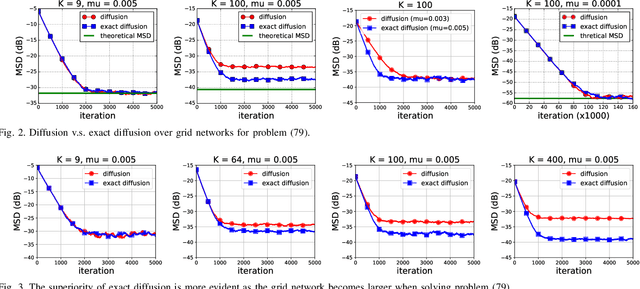
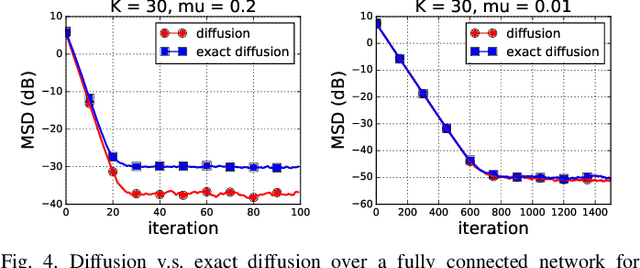
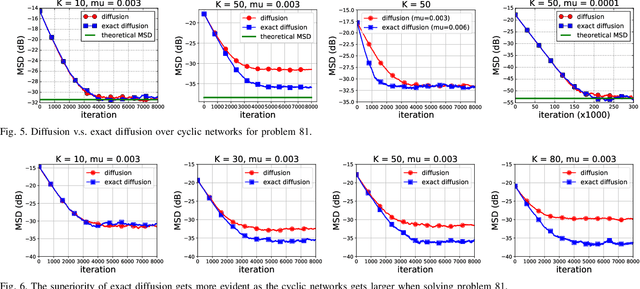
Various bias-correction methods such as EXTRA, DIGing, and exact diffusion have been proposed recently to solve distributed deterministic optimization problems. These methods employ constant step-sizes and converge linearly to the {\em exact} solution under proper conditions. However, their performance under stochastic and adaptive settings remains unclear. It is still unknown whether the bias-correction is necessary over adaptive networks. By studying exact diffusion and examining its steady-state performance under stochastic scenarios, this paper provides affirmative results. It is shown that the correction step in exact diffusion leads to better steady-state performance than traditional methods. It is also analytically shown the superiority of exact diffusion is more evident over badly-connected network topologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge