Variance-Reduced Stochastic Learning by Networked Agents under Random Reshuffling

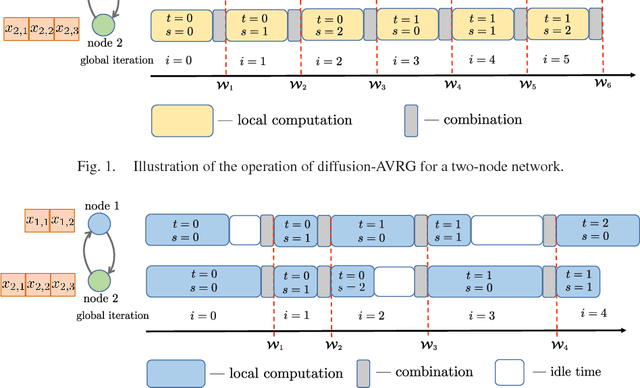
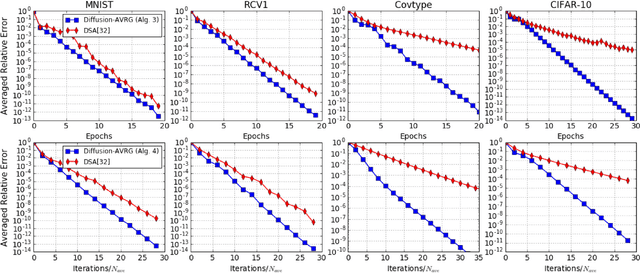
A new amortized variance-reduced gradient (AVRG) algorithm was developed in \cite{ying2017convergence}, which has constant storage requirement in comparison to SAGA and balanced gradient computations in comparison to SVRG. One key advantage of the AVRG strategy is its amenability to decentralized implementations. In this work, we show how AVRG can be extended to the network case where multiple learning agents are assumed to be connected by a graph topology. In this scenario, each agent observes data that is spatially distributed and all agents are only allowed to communicate with direct neighbors. Moreover, the amount of data observed by the individual agents may differ drastically. For such situations, the balanced gradient computation property of AVRG becomes a real advantage in reducing idle time caused by unbalanced local data storage requirements, which is characteristic of other reduced-variance gradient algorithms. The resulting diffusion-AVRG algorithm is shown to have linear convergence to the exact solution, and is much more memory efficient than other alternative algorithms. In addition, we propose a mini-batch strategy to balance the communication and computation efficiency for diffusion-AVRG. When a proper batch size is employed, it is observed in simulations that diffusion-AVRG is more computationally efficient than exact diffusion or EXTRA while maintaining almost the same communication efficiency.