A non-asymptotic theory of Kernel Ridge Regression: deterministic equivalents, test error, and GCV estimator

We consider learning an unknown target function $f_*$ using kernel ridge regression (KRR) given i.i.d. data $(u_i,y_i)$, $i\leq n$, where $u_i \in U$ is a covariate vector and $y_i = f_* (u_i) +\varepsilon_i \in \mathbb{R}$. A recent string of work has empirically shown that the test error of KRR can be well approximated by a closed-form estimate derived from an `equivalent' sequence model that only depends on the spectrum of the kernel operator. However, a theoretical justification for this equivalence has so far relied either on restrictive assumptions -- such as subgaussian independent eigenfunctions -- , or asymptotic derivations for specific kernels in high dimensions. In this paper, we prove that this equivalence holds for a general class of problems satisfying some spectral and concentration properties on the kernel eigendecomposition. Specifically, we establish in this setting a non-asymptotic deterministic approximation for the test error of KRR -- with explicit non-asymptotic bounds -- that only depends on the eigenvalues and the target function alignment to the eigenvectors of the kernel. Our proofs rely on a careful derivation of deterministic equivalents for random matrix functionals in the dimension free regime pioneered by Cheng and Montanari (2022). We apply this setting to several classical examples and show an excellent agreement between theoretical predictions and numerical simulations. These results rely on having access to the eigendecomposition of the kernel operator. Alternatively, we prove that, under this same setting, the generalized cross-validation (GCV) estimator concentrates on the test error uniformly over a range of ridge regularization parameter that includes zero (the interpolating solution). As a consequence, the GCV estimator can be used to estimate from data the test error and optimal regularization parameter for KRR.

Universality of max-margin classifiers

Maximum margin binary classification is one of the most fundamental algorithms in machine learning, yet the role of featurization maps and the high-dimensional asymptotics of the misclassification error for non-Gaussian features are still poorly understood. We consider settings in which we observe binary labels $y_i$ and either $d$-dimensional covariates ${\boldsymbol z}_i$ that are mapped to a $p$-dimension space via a randomized featurization map ${\boldsymbol \phi}:\mathbb{R}^d \to\mathbb{R}^p$, or $p$-dimensional features of non-Gaussian independent entries. In this context, we study two fundamental questions: $(i)$ At what overparametrization ratio $p/n$ do the data become linearly separable? $(ii)$ What is the generalization error of the max-margin classifier? Working in the high-dimensional regime in which the number of features $p$, the number of samples $n$ and the input dimension $d$ (in the nonlinear featurization setting) diverge, with ratios of order one, we prove a universality result establishing that the asymptotic behavior is completely determined by the expected covariance of feature vectors and by the covariance between features and labels. In particular, the overparametrization threshold and generalization error can be computed within a simpler Gaussian model. The main technical challenge lies in the fact that max-margin is not the maximizer (or minimizer) of an empirical average, but the maximizer of a minimum over the samples. We address this by representing the classifier as an average over support vectors. Crucially, we find that in high dimensions, the support vector count is proportional to the number of samples, which ultimately yields universality.

Universality of empirical risk minimization

Consider supervised learning from i.i.d. samples $\{{\boldsymbol x}_i,y_i\}_{i\le n}$ where ${\boldsymbol x}_i \in\mathbb{R}^p$ are feature vectors and ${y} \in \mathbb{R}$ are labels. We study empirical risk minimization over a class of functions that are parameterized by $\mathsf{k} = O(1)$ vectors ${\boldsymbol \theta}_1, . . . , {\boldsymbol \theta}_{\mathsf k} \in \mathbb{R}^p$ , and prove universality results both for the training and test error. Namely, under the proportional asymptotics $n,p\to\infty$, with $n/p = \Theta(1)$, we prove that the training error depends on the random features distribution only through its covariance structure. Further, we prove that the minimum test error over near-empirical risk minimizers enjoys similar universality properties. In particular, the asymptotics of these quantities can be computed $-$to leading order$-$ under a simpler model in which the feature vectors ${\boldsymbol x}_i$ are replaced by Gaussian vectors ${\boldsymbol g}_i$ with the same covariance. Earlier universality results were limited to strongly convex learning procedures, or to feature vectors ${\boldsymbol x}_i$ with independent entries. Our results do not make any of these assumptions. Our assumptions are general enough to include feature vectors ${\boldsymbol x}_i$ that are produced by randomized featurization maps. In particular we explicitly check the assumptions for certain random features models (computing the output of a one-layer neural network with random weights) and neural tangent models (first-order Taylor approximation of two-layer networks).

Causal Structure Discovery from Distributions Arising from Mixtures of DAGs

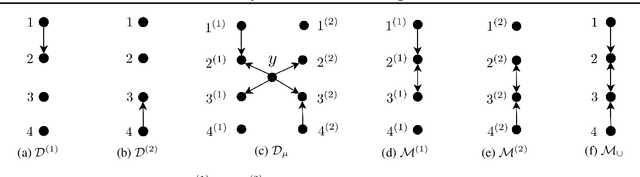
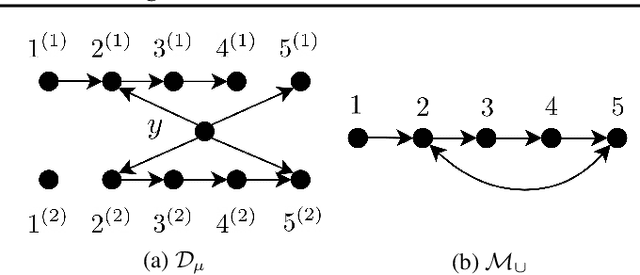
We consider distributions arising from a mixture of causal models, where each model is represented by a directed acyclic graph (DAG). We provide a graphical representation of such mixture distributions and prove that this representation encodes the conditional independence relations of the mixture distribution. We then consider the problem of structure learning based on samples from such distributions. Since the mixing variable is latent, we consider causal structure discovery algorithms such as FCI that can deal with latent variables. We show that such algorithms recover a "union" of the component DAGs and can identify variables whose conditional distribution across the component DAGs vary. We demonstrate our results on synthetic and real data showing that the inferred graph identifies nodes that vary between the different mixture components. As an immediate application, we demonstrate how retrieval of this causal information can be used to cluster samples according to each mixture component.

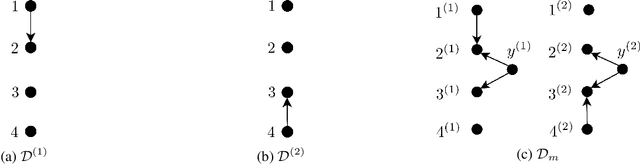
Ordering-Based Causal Structure Learning in the Presence of Latent Variables

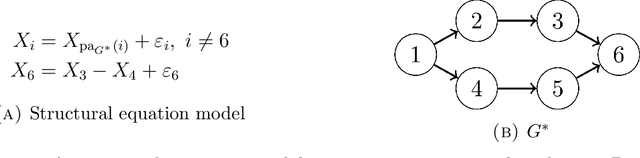
We consider the task of learning a causal graph in the presence of latent confounders given i.i.d.~samples from the model. While current algorithms for causal structure discovery in the presence of latent confounders are constraint-based, we here propose a score-based approach. We prove that under assumptions weaker than faithfulness, any sparsest independence map (IMAP) of the distribution belongs to the Markov equivalence class of the true model. This motivates the \emph{Sparsest Poset} formulation - that posets can be mapped to minimal IMAPs of the true model such that the sparsest of these IMAPs is Markov equivalent to the true model. Motivated by this result, we propose a greedy algorithm over the space of posets for causal structure discovery in the presence of latent confounders and compare its performance to the current state-of-the-art algorithms FCI and FCI+ on synthetic data.

Explaining intuitive difficulty judgments by modeling physical effort and risk

The ability to estimate task difficulty is critical for many real-world decisions such as setting appropriate goals for ourselves or appreciating others' accomplishments. Here we give a computational account of how humans judge the difficulty of a range of physical construction tasks (e.g., moving 10 loose blocks from their initial configuration to their target configuration, such as a vertical tower) by quantifying two key factors that influence construction difficulty: physical effort and physical risk. Physical effort captures the minimal work needed to transport all objects to their final positions, and is computed using a hybrid task-and-motion planner. Physical risk corresponds to stability of the structure, and is computed using noisy physics simulations to capture the costs for precision (e.g., attention, coordination, fine motor movements) required for success. We show that the full effort-risk model captures human estimates of difficulty and construction time better than either component alone.

Physical problem solving: Joint planning with symbolic, geometric, and dynamic constraints

In this paper, we present a new task that investigates how people interact with and make judgments about towers of blocks. In Experiment~1, participants in the lab solved a series of problems in which they had to re-configure three blocks from an initial to a final configuration. We recorded whether they used one hand or two hands to do so. In Experiment~2, we asked participants online to judge whether they think the person in the lab used one or two hands. The results revealed a close correspondence between participants' actions in the lab, and the mental simulations of participants online. To explain participants' actions and mental simulations, we develop a model that plans over a symbolic representation of the situation, executes the plan using a geometric solver, and checks the plan's feasibility by taking into account the physical constraints of the scene. Our model explains participants' actions and judgments to a high degree of quantitative accuracy.