Universality of max-margin classifiers

Maximum margin binary classification is one of the most fundamental algorithms in machine learning, yet the role of featurization maps and the high-dimensional asymptotics of the misclassification error for non-Gaussian features are still poorly understood. We consider settings in which we observe binary labels $y_i$ and either $d$-dimensional covariates ${\boldsymbol z}_i$ that are mapped to a $p$-dimension space via a randomized featurization map ${\boldsymbol \phi}:\mathbb{R}^d \to\mathbb{R}^p$, or $p$-dimensional features of non-Gaussian independent entries. In this context, we study two fundamental questions: $(i)$ At what overparametrization ratio $p/n$ do the data become linearly separable? $(ii)$ What is the generalization error of the max-margin classifier? Working in the high-dimensional regime in which the number of features $p$, the number of samples $n$ and the input dimension $d$ (in the nonlinear featurization setting) diverge, with ratios of order one, we prove a universality result establishing that the asymptotic behavior is completely determined by the expected covariance of feature vectors and by the covariance between features and labels. In particular, the overparametrization threshold and generalization error can be computed within a simpler Gaussian model. The main technical challenge lies in the fact that max-margin is not the maximizer (or minimizer) of an empirical average, but the maximizer of a minimum over the samples. We address this by representing the classifier as an average over support vectors. Crucially, we find that in high dimensions, the support vector count is proportional to the number of samples, which ultimately yields universality.

The generalization error of max-margin linear classifiers: High-dimensional asymptotics in the overparametrized regime

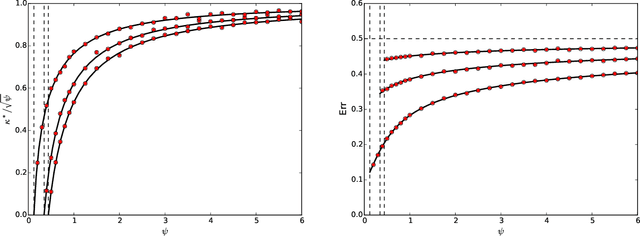
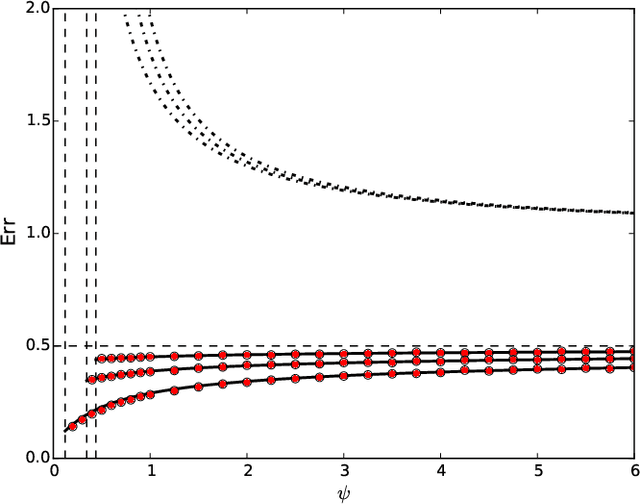
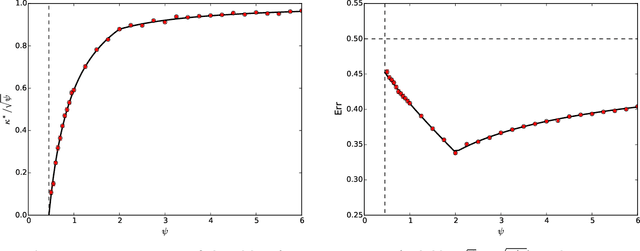
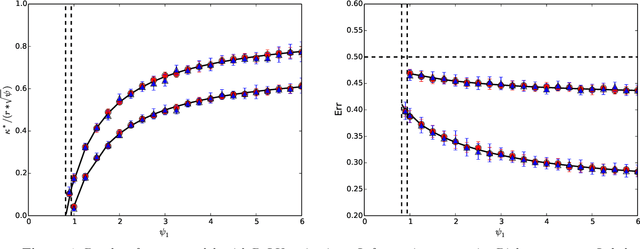
Modern machine learning models are often so complex that they achieve vanishing classification error on the training set. Max-margin linear classifiers are among the simplest classification methods that have zero training error (with linearly separable data). Despite this simplicity, their high-dimensional behavior is not yet completely understood. We assume to be given i.i.d. data $(y_i,{\boldsymbol x}_i)$, $i\le n$ with ${\boldsymbol x}_i\sim {\sf N}({\boldsymbol 0},{\boldsymbol \Sigma})$ a $p$-dimensional Gaussian feature vector, and $y_i \in\{+1,-1\}$ a label whose distribution depends on a linear combination of the covariates $\langle {\boldsymbol \theta}_*,{\boldsymbol x}_i\rangle$. We consider the proportional asymptotics $n,p\to\infty$ with $p/n\to \psi$, and derive exact expressions for the limiting prediction error. Our asymptotic results match simulations already when $n,p$ are of the order of a few hundreds. We explore several choices for the the pair $({\boldsymbol \theta}_*,{\boldsymbol \Sigma})$, and show that the resulting generalization curve (test error error as a function of the overparametrization ratio $\psi=p/n$) is qualitatively different, depending on this choice. In particular we consider a specific structure of $({\boldsymbol \theta}_*,{\boldsymbol \Sigma})$ that captures the behavior of nonlinear random feature models or, equivalently, two-layers neural networks with random first layer weights. In this case, we observe that the test error is monotone decreasing in the number of parameters. This finding agrees with the recently developed `double descent' phenomenology for overparametrized models.