Maximum likelihood thresholds of Gaussian graphical models and graphical lasso

Associated to each graph G is a Gaussian graphical model. Such models are often used in high-dimensional settings, i.e. where there are relatively few data points compared to the number of variables. The maximum likelihood threshold of a graph is the minimum number of data points required to fit the corresponding graphical model using maximum likelihood estimation. Graphical lasso is a method for selecting and fitting a graphical model. In this project, we ask: when graphical lasso is used to select and fit a graphical model on n data points, how likely is it that n is greater than or equal to the maximum likelihood threshold of the corresponding graph? Our results are a series of computational experiments.

Ordering-Based Causal Structure Learning in the Presence of Latent Variables

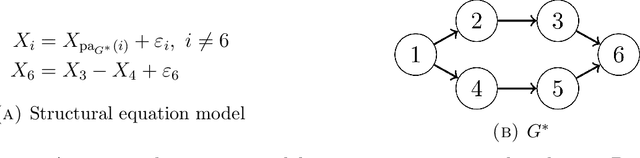
We consider the task of learning a causal graph in the presence of latent confounders given i.i.d.~samples from the model. While current algorithms for causal structure discovery in the presence of latent confounders are constraint-based, we here propose a score-based approach. We prove that under assumptions weaker than faithfulness, any sparsest independence map (IMAP) of the distribution belongs to the Markov equivalence class of the true model. This motivates the \emph{Sparsest Poset} formulation - that posets can be mapped to minimal IMAPs of the true model such that the sparsest of these IMAPs is Markov equivalent to the true model. Motivated by this result, we propose a greedy algorithm over the space of posets for causal structure discovery in the presence of latent confounders and compare its performance to the current state-of-the-art algorithms FCI and FCI+ on synthetic data.