Frequency and Generalisation of Periodic Activation Functions in Reinforcement Learning

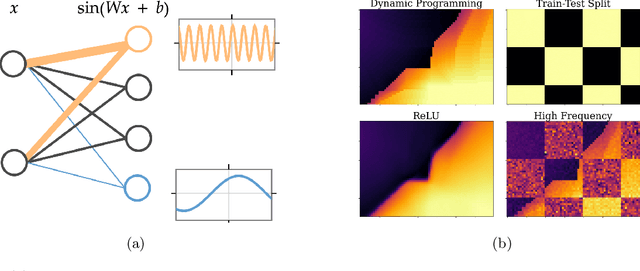
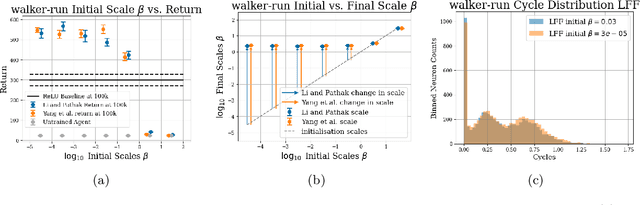
Periodic activation functions, often referred to as learned Fourier features have been widely demonstrated to improve sample efficiency and stability in a variety of deep RL algorithms. Potentially incompatible hypotheses have been made about the source of these improvements. One is that periodic activations learn low frequency representations and as a result avoid overfitting to bootstrapped targets. Another is that periodic activations learn high frequency representations that are more expressive, allowing networks to quickly fit complex value functions. We analyse these claims empirically, finding that periodic representations consistently converge to high frequencies regardless of their initialisation frequency. We also find that while periodic activation functions improve sample efficiency, they exhibit worse generalization on states with added observation noise -- especially when compared to otherwise equivalent networks with ReLU activation functions. Finally, we show that weight decay regularization is able to partially offset the overfitting of periodic activation functions, delivering value functions that learn quickly while also generalizing.

Towards Automated Circuit Discovery for Mechanistic Interpretability

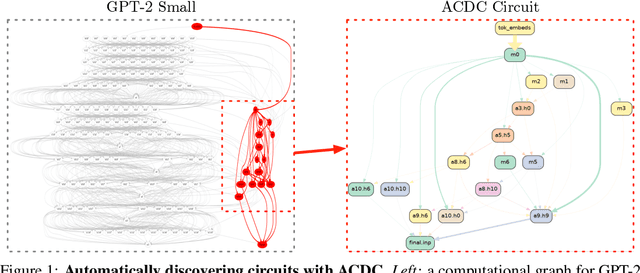
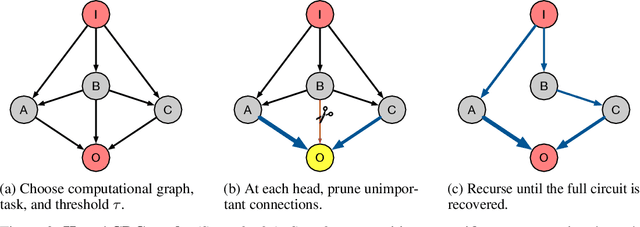
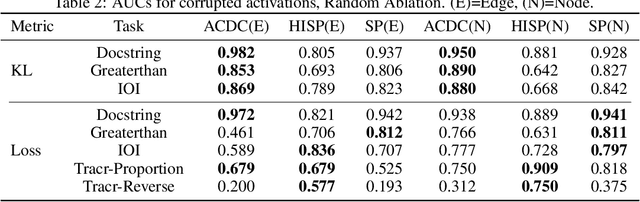
Recent work in mechanistic interpretability has reverse-engineered nontrivial behaviors of transformer models. These contributions required considerable effort and researcher intuition, which makes it difficult to apply the same methods to understand the complex behavior that current models display. At their core however, the workflow for these discoveries is surprisingly similar. Researchers create a data set and metric that elicit the desired model behavior, subdivide the network into appropriate abstract units, replace activations of those units to identify which are involved in the behavior, and then interpret the functions that these units implement. By varying the data set, metric, and units under investigation, researchers can understand the functionality of each neural network region and the circuits they compose. This work proposes a novel algorithm, Automatic Circuit DisCovery (ACDC), to automate the identification of the important units in the network. Given a model's computational graph, ACDC finds subgraphs that explain a behavior of the model. ACDC was able to reproduce a previously identified circuit for Python docstrings in a small transformer, identifying 6/7 important attention heads that compose up to 3 layers deep, while including 91% fewer the connections.

A Simple Approach for State-Action Abstraction using a Learned MDP Homomorphism

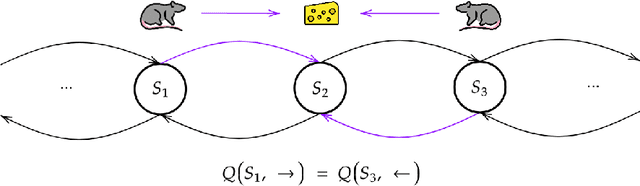
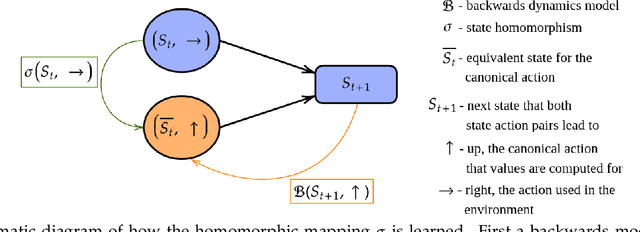
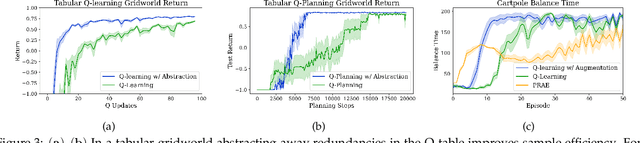
Animals are able to rapidly infer from limited experience when sets of state action pairs have equivalent reward and transition dynamics. On the other hand, modern reinforcement learning systems must painstakingly learn through trial and error that sets of state action pairs are value equivalent -- requiring an often prohibitively large amount of samples from their environment. MDP homomorphisms have been proposed that reduce the observed MDP of an environment to an abstract MDP, which can enable more sample efficient policy learning. Consequently, impressive improvements in sample efficiency have been achieved when a suitable MDP homomorphism can be constructed a priori -- usually by exploiting a practioner's knowledge of environment symmetries. We propose a novel approach to constructing a homomorphism in discrete action spaces, which uses a partial model of environment dynamics to infer which state action pairs lead to the same state -- reducing the size of the state-action space by a factor equal to the cardinality of the action space. We call this method equivalent effect abstraction. In a gridworld setting, we demonstrate empirically that equivalent effect abstraction can improve sample efficiency in a model-free setting and planning efficiency for modelbased approaches. Furthermore, we show on cartpole that our approach outperforms an existing method for learning homomorphisms, while using 33x less training data.

Scattering Networks on the Sphere for Scalable and Rotationally Equivariant Spherical CNNs

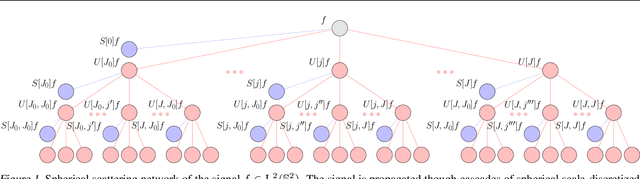
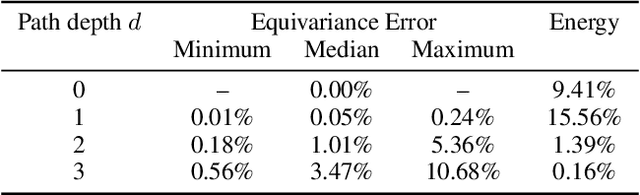
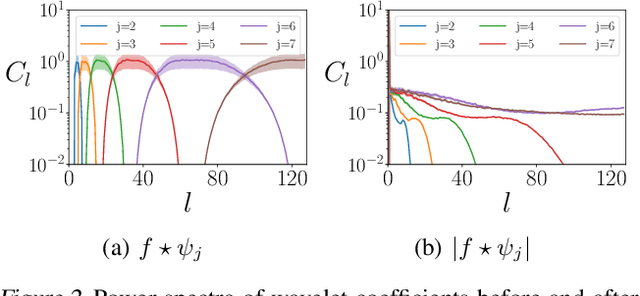
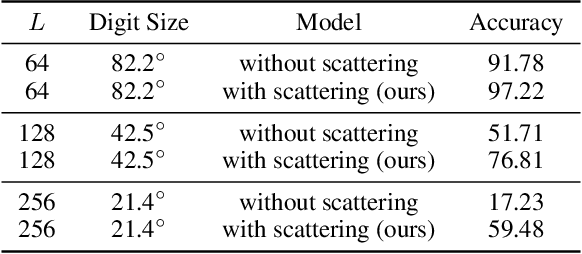
Convolutional neural networks (CNNs) constructed natively on the sphere have been developed recently and shown to be highly effective for the analysis of spherical data. While an efficient framework has been formulated, spherical CNNs are nevertheless highly computationally demanding; typically they cannot scale beyond spherical signals of thousands of pixels. We develop scattering networks constructed natively on the sphere that provide a powerful representational space for spherical data. Spherical scattering networks are computationally scalable and exhibit rotational equivariance, while their representational space is invariant to isometries and provides efficient and stable signal representations. By integrating scattering networks as an additional type of layer in the generalized spherical CNN framework, we show how they can be leveraged to scale spherical CNNs to the high-resolution data typical of many practical applications, with spherical signals of many tens of megapixels and beyond.

Escaping Stochastic Traps with Aleatoric Mapping Agents

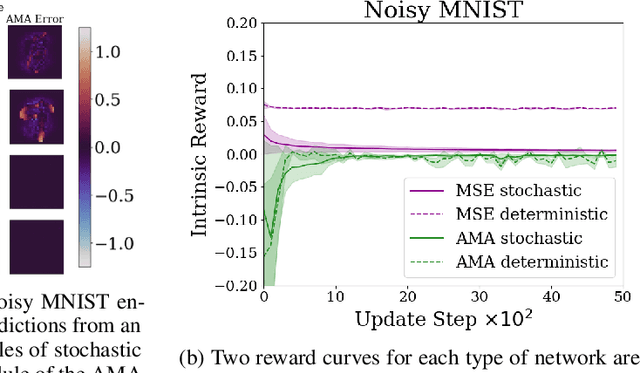
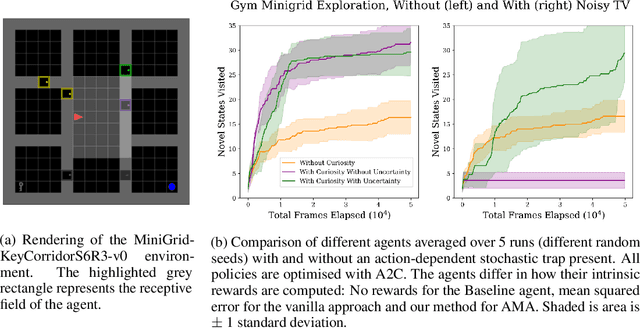
Exploration in environments with sparse rewards is difficult for artificial agents. Curiosity driven learning -- using feed-forward prediction errors as intrinsic rewards -- has achieved some success in these scenarios, but fails when faced with action-dependent noise sources. We present aleatoric mapping agents (AMAs), a neuroscience inspired solution modeled on the cholinergic system of the mammalian brain. AMAs aim to explicitly ascertain which dynamics of the environment are unpredictable, regardless of whether those dynamics are induced by the actions of the agent. This is achieved by generating separate forward predictions for the mean and variance of future states and reducing intrinsic rewards for those transitions with high aleatoric variance. We show AMAs are able to effectively circumvent action-dependent stochastic traps that immobilise conventional curiosity driven agents. The code for all experiments presented in this paper is open sourced: http://github.com/self-supervisor/Escaping-Stochastic-Traps-With-Aleatoric-Mapping-Agents.

Efficient Generalized Spherical CNNs

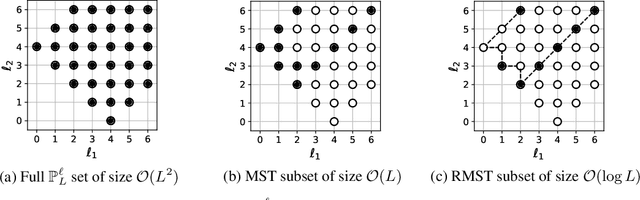
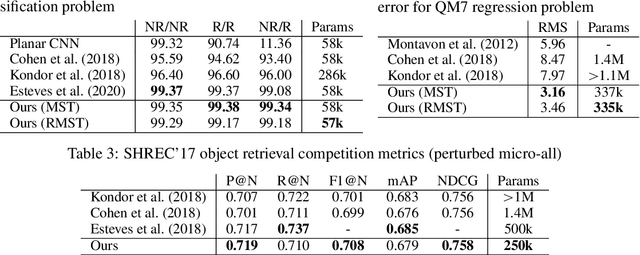
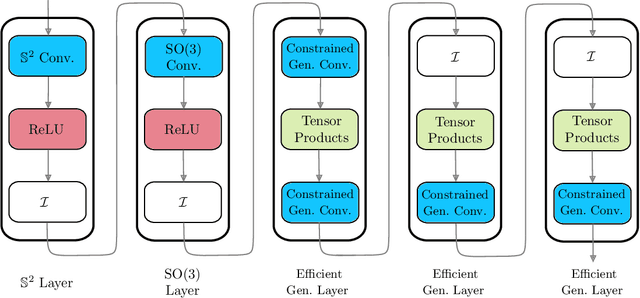
Many problems across computer vision and the natural sciences require the analysis of spherical data, for which representations may be learned efficiently by encoding equivariance to rotational symmetries. We present a generalized spherical CNN framework that encompasses various existing approaches and allows them to be leveraged alongside each other. The only existing non-linear spherical CNN layer that is strictly equivariant has complexity $\mathcal{O}(C^2L^5)$, where $C$ is a measure of representational capacity and $L$ the spherical harmonic bandlimit. Such a high computational cost often prohibits the use of strictly equivariant spherical CNNs. We develop two new strictly equivariant layers with reduced complexity $\mathcal{O}(CL^4)$ and $\mathcal{O}(CL^3 \log L)$, making larger, more expressive models computationally feasible. Moreover, we adopt efficient sampling theory to achieve further computational savings. We show that these developments allow the construction of more expressive hybrid models that achieve state-of-the-art accuracy and parameter efficiency on spherical benchmark problems.