Frequency and Generalisation of Periodic Activation Functions in Reinforcement Learning

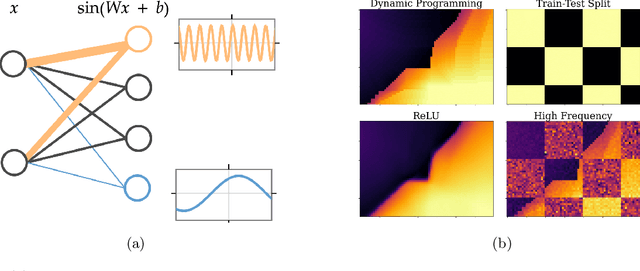
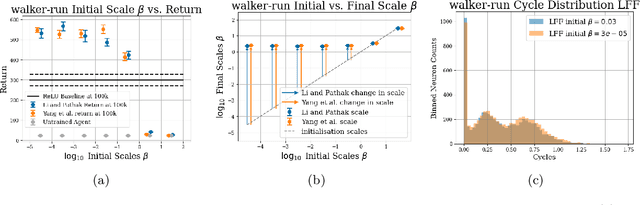
Periodic activation functions, often referred to as learned Fourier features have been widely demonstrated to improve sample efficiency and stability in a variety of deep RL algorithms. Potentially incompatible hypotheses have been made about the source of these improvements. One is that periodic activations learn low frequency representations and as a result avoid overfitting to bootstrapped targets. Another is that periodic activations learn high frequency representations that are more expressive, allowing networks to quickly fit complex value functions. We analyse these claims empirically, finding that periodic representations consistently converge to high frequencies regardless of their initialisation frequency. We also find that while periodic activation functions improve sample efficiency, they exhibit worse generalization on states with added observation noise -- especially when compared to otherwise equivalent networks with ReLU activation functions. Finally, we show that weight decay regularization is able to partially offset the overfitting of periodic activation functions, delivering value functions that learn quickly while also generalizing.

A Boundary Tilting Persepective on the Phenomenon of Adversarial Examples

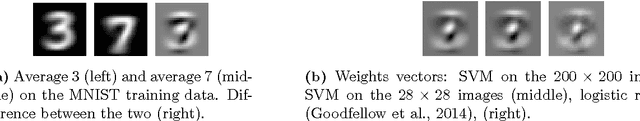
Deep neural networks have been shown to suffer from a surprising weakness: their classification outputs can be changed by small, non-random perturbations of their inputs. This adversarial example phenomenon has been explained as originating from deep networks being "too linear" (Goodfellow et al., 2014). We show here that the linear explanation of adversarial examples presents a number of limitations: the formal argument is not convincing, linear classifiers do not always suffer from the phenomenon, and when they do their adversarial examples are different from the ones affecting deep networks. We propose a new perspective on the phenomenon. We argue that adversarial examples exist when the classification boundary lies close to the submanifold of sampled data, and present a mathematical analysis of this new perspective in the linear case. We define the notion of adversarial strength and show that it can be reduced to the deviation angle between the classifier considered and the nearest centroid classifier. Then, we show that the adversarial strength can be made arbitrarily high independently of the classification performance due to a mechanism that we call boundary tilting. This result leads us to defining a new taxonomy of adversarial examples. Finally, we show that the adversarial strength observed in practice is directly dependent on the level of regularisation used and the strongest adversarial examples, symptomatic of overfitting, can be avoided by using a proper level of regularisation.