CNLL: A Semi-supervised Approach For Continual Noisy Label Learning

The task of continual learning requires careful design of algorithms that can tackle catastrophic forgetting. However, the noisy label, which is inevitable in a real-world scenario, seems to exacerbate the situation. While very few studies have addressed the issue of continual learning under noisy labels, long training time and complicated training schemes limit their applications in most cases. In contrast, we propose a simple purification technique to effectively cleanse the online data stream that is both cost-effective and more accurate. After purification, we perform fine-tuning in a semi-supervised fashion that ensures the participation of all available samples. Training in this fashion helps us learn a better representation that results in state-of-the-art (SOTA) performance. Through extensive experimentation on 3 benchmark datasets, MNIST, CIFAR10 and CIFAR100, we show the effectiveness of our proposed approach. We achieve a 24.8% performance gain for CIFAR10 with 20% noise over previous SOTA methods. Our code is publicly available.

RODD: A Self-Supervised Approach for Robust Out-of-Distribution Detection

Recent studies have addressed the concern of detecting and rejecting the out-of-distribution (OOD) samples as a major challenge in the safe deployment of deep learning (DL) models. It is desired that the DL model should only be confident about the in-distribution (ID) data which reinforces the driving principle of the OOD detection. In this paper, we propose a simple yet effective generalized OOD detection method independent of out-of-distribution datasets. Our approach relies on self-supervised feature learning of the training samples, where the embeddings lie on a compact low-dimensional space. Motivated by the recent studies that show self-supervised adversarial contrastive learning helps robustify the model, we empirically show that a pre-trained model with self-supervised contrastive learning yields a better model for uni-dimensional feature learning in the latent space. The method proposed in this work referred to as RODD outperforms SOTA detection performance on an extensive suite of benchmark datasets on OOD detection tasks. On the CIFAR-100 benchmarks, RODD achieves a 26.97 $\%$ lower false-positive rate (FPR@95) compared to SOTA methods.

Generative Model Adversarial Training for Deep Compressed Sensing

Deep compressed sensing assumes the data has sparse representation in a latent space, i.e., it is intrinsically of low-dimension. The original data is assumed to be mapped from a low-dimensional space through a low-to-high-dimensional generator. In this work, we propound how to design such a low-to-high dimensional deep learning-based generator suiting for compressed sensing, while satisfying robustness to universal adversarial perturbations in the latent domain. We also justify why the noise is considered in the latent space. The work is also buttressed with theoretical analysis on the robustness of the trained generator to adversarial perturbations. Experiments on real-world datasets are provided to substantiate the efficacy of the proposed \emph{generative model adversarial training for deep compressed sensing.}

Two-way Spectrum Pursuit for CUR Decomposition and Its Application in Joint Column/Row Subset Selection

The problem of simultaneous column and row subset selection is addressed in this paper. The column space and row space of a matrix are spanned by its left and right singular vectors, respectively. However, the singular vectors are not within actual columns/rows of the matrix. In this paper, an iterative approach is proposed to capture the most structural information of columns/rows via selecting a subset of actual columns/rows. This algorithm is referred to as two-way spectrum pursuit (TWSP) which provides us with an accurate solution for the CUR matrix decomposition. TWSP is applicable in a wide range of applications since it enjoys a linear complexity w.r.t. number of original columns/rows. We demonstrated the application of TWSP for joint channel and sensor selection in cognitive radio networks, informative users and contents detection, and efficient supervised data reduction.

LSDAT: Low-Rank and Sparse Decomposition for Decision-based Adversarial Attack

We propose LSDAT, an image-agnostic decision-based black-box attack that exploits low-rank and sparse decomposition (LSD) to dramatically reduce the number of queries and achieve superior fooling rates compared to the state-of-the-art decision-based methods under given imperceptibility constraints. LSDAT crafts perturbations in the low-dimensional subspace formed by the sparse component of the input sample and that of an adversarial sample to obtain query-efficiency. The specific perturbation of interest is obtained by traversing the path between the input and adversarial sparse components. It is set forth that the proposed sparse perturbation is the most aligned sparse perturbation with the shortest path from the input sample to the decision boundary for some initial adversarial sample (the best sparse approximation of shortest path, likely to fool the model). Theoretical analyses are provided to justify the functionality of LSDAT. Unlike other dimensionality reduction based techniques aimed at improving query efficiency (e.g, ones based on FFT), LSD works directly in the image pixel domain to guarantee that non-$\ell_2$ constraints, such as sparsity, are satisfied. LSD offers better control over the number of queries and provides computational efficiency as it performs sparse decomposition of the input and adversarial images only once to generate all queries. We demonstrate $\ell_0$, $\ell_2$ and $\ell_\infty$ bounded attacks with LSDAT to evince its efficiency compared to baseline decision-based attacks in diverse low-query budget scenarios as outlined in the experiments.

A Novel Approach to Sparse Inverse Covariance Estimation Using Transform Domain Updates and Exponentially Adaptive Thresholding

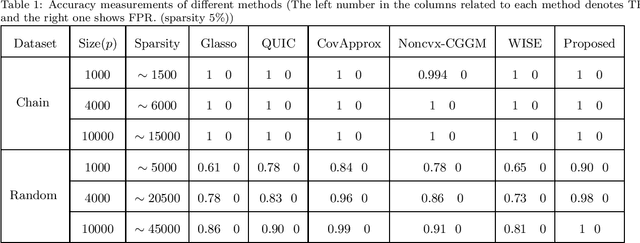
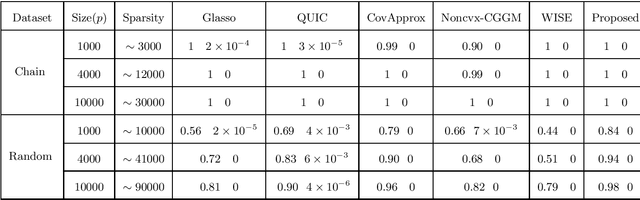
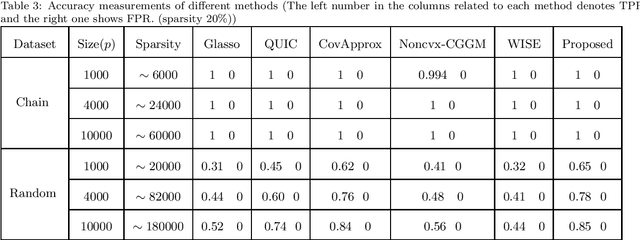
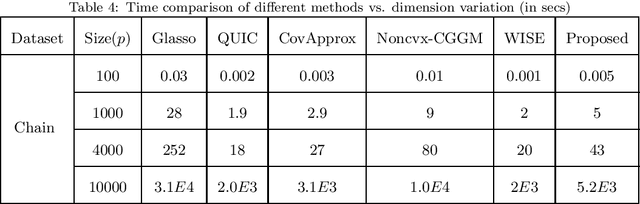
Sparse Inverse Covariance Estimation (SICE) is useful in many practical data analyses. Recovering the connectivity, non-connectivity graph of covariates is classified amongst the most important data mining and learning problems. In this paper, we introduce a novel SICE approach using adaptive thresholding. Our method is based on updates in a transformed domain of the desired matrix and exponentially decaying adaptive thresholding in the main domain (Inverse Covariance matrix domain). In addition to the proposed algorithm, the convergence analysis is also provided. In the Numerical Experiments Section, we show that the proposed method outperforms state-of-the-art methods in terms of accuracy.

A Novel Approach to Quantized Matrix Completion Using Huber Loss Measure

In this paper, we introduce a novel and robust approach to Quantized Matrix Completion (QMC). First, we propose a rank minimization problem with constraints induced by quantization bounds. Next, we form an unconstrained optimization problem by regularizing the rank function with Huber loss. Huber loss is leveraged to control the violation from quantization bounds due to two properties: 1- It is differentiable, 2- It is less sensitive to outliers than the quadratic loss. A Smooth Rank Approximation is utilized to endorse lower rank on the genuine data matrix. Thus, an unconstrained optimization problem with differentiable objective function is obtained allowing us to advantage from Gradient Descent (GD) technique. Novel and firm theoretical analysis on problem model and convergence of our algorithm to the global solution are provided. Another contribution of our work is that our method does not require projections or initial rank estimation unlike the state- of-the-art. In the Numerical Experiments Section, the noticeable outperformance of our proposed method in learning accuracy and computational complexity compared to those of the state-of- the-art literature methods is illustrated as the main contribution.

Recovering Quantized Data with Missing Information Using Bilinear Factorization and Augmented Lagrangian Method

In this paper, we propose a novel approach in order to recover a quantized matrix with missing information. We propose a regularized convex cost function composed of a log-likelihood term and a Trace norm term. The Bi-factorization approach and the Augmented Lagrangian Method (ALM) are applied to find the global minimizer of the cost function in order to recover the genuine data. We provide mathematical convergence analysis for our proposed algorithm. In the Numerical Experiments Section, we show the superiority of our method in accuracy and also its robustness in computational complexity compared to the state-of-the-art literature methods.

Transduction with Matrix Completion Using Smoothed Rank Function

In this paper, we propose two new algorithms for transduction with Matrix Completion (MC) problem. The joint MC and prediction tasks are addressed simultaneously to enhance the accuracy, i.e., the label matrix is concatenated to the data matrix forming a stacked matrix. Assuming the data matrix is of low rank, we propose new recommendation methods by posing the problem as a constrained minimization of the Smoothed Rank Function (SRF). We provide convergence analysis for the proposed algorithms. The simulations are conducted on real datasets in two different scenarios of randomly missing pattern with and without block loss. The results confirm that the accuracy of our proposed methods outperforms those of state-of-the-art methods even up to 10% in low observation rates for the scenario without block loss. Our accuracy in the latter scenario, is comparable to state-of-the-art methods while the complexity of the proposed algorithms are reduced up to 4 times.

OBTAIN: Real-Time Beat Tracking in Audio Signals

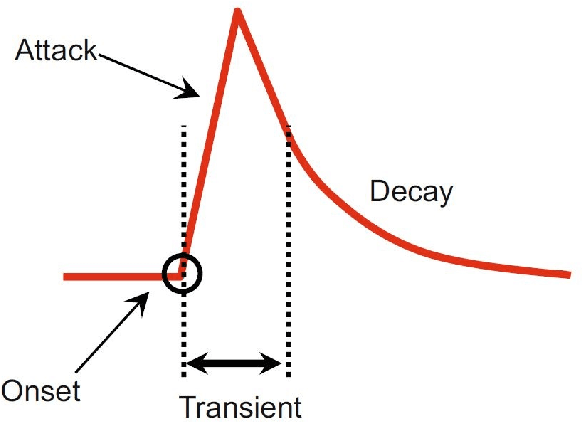
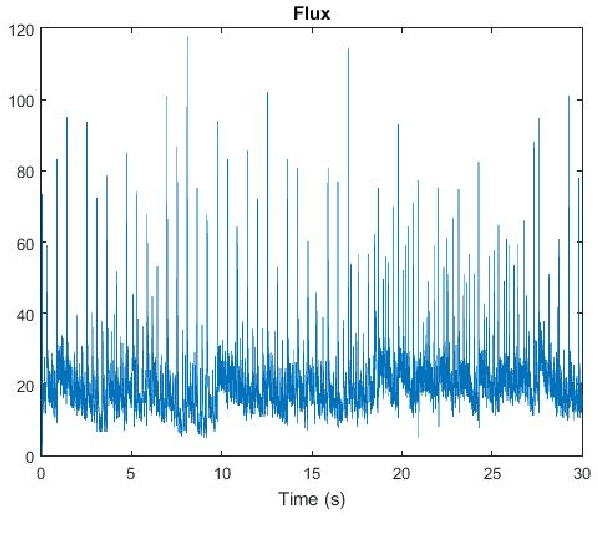
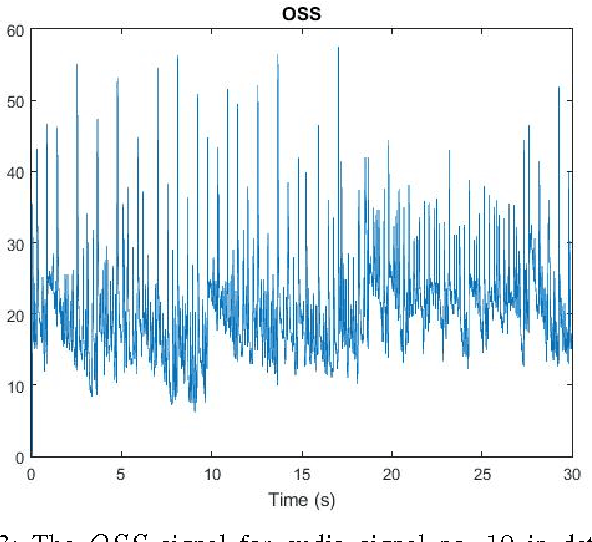
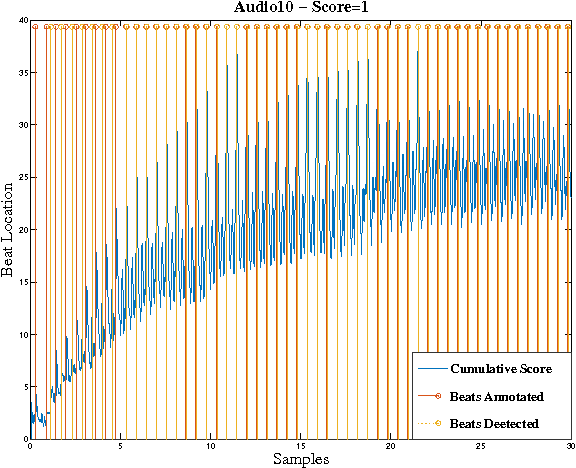
In this paper, we design a system in order to perform the real-time beat tracking for an audio signal. We use Onset Strength Signal (OSS) to detect the onsets and estimate the tempos. Then, we form Cumulative Beat Strength Signal (CBSS) by taking advantage of OSS and estimated tempos. Next, we perform peak detection by extracting the periodic sequence of beats among all CBSS peaks. In simulations, we can see that our proposed algorithm, Online Beat TrAckINg (OBTAIN), outperforms state-of-art results in terms of prediction accuracy while maintaining comparable and practical computational complexity. The real-time performance is tractable visually as illustrated in the simulations.