Transduction with Matrix Completion Using Smoothed Rank Function

In this paper, we propose two new algorithms for transduction with Matrix Completion (MC) problem. The joint MC and prediction tasks are addressed simultaneously to enhance the accuracy, i.e., the label matrix is concatenated to the data matrix forming a stacked matrix. Assuming the data matrix is of low rank, we propose new recommendation methods by posing the problem as a constrained minimization of the Smoothed Rank Function (SRF). We provide convergence analysis for the proposed algorithms. The simulations are conducted on real datasets in two different scenarios of randomly missing pattern with and without block loss. The results confirm that the accuracy of our proposed methods outperforms those of state-of-the-art methods even up to 10% in low observation rates for the scenario without block loss. Our accuracy in the latter scenario, is comparable to state-of-the-art methods while the complexity of the proposed algorithms are reduced up to 4 times.

New Methods of Enhancing Prediction Accuracy in Linear Models with Missing Data

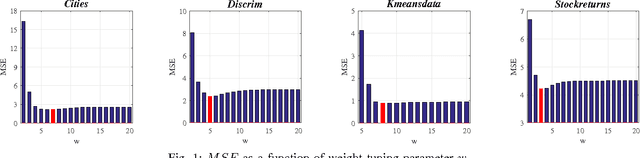
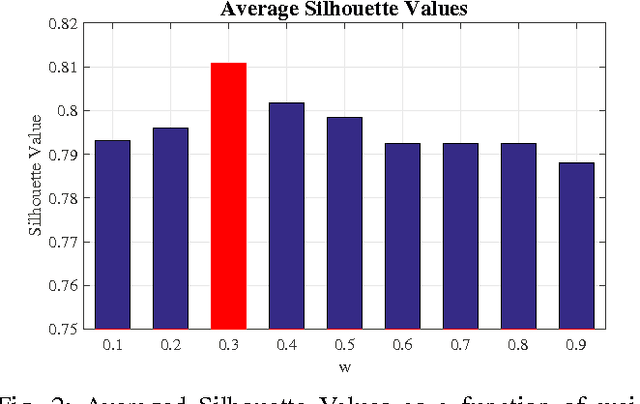
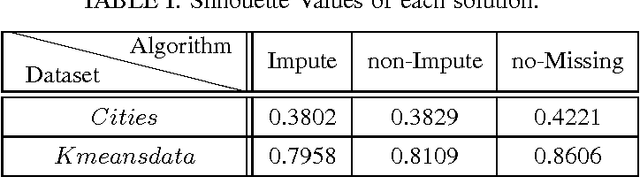
In this paper, prediction for linear systems with missing information is investigated. New methods are introduced to improve the Mean Squared Error (MSE) on the test set in comparison to state-of-the-art methods, through appropriate tuning of Bias-Variance trade-off. First, the use of proposed Soft Weighted Prediction (SWP) algorithm and its efficacy are depicted and compared to previous works for non-missing scenarios. The algorithm is then modified and optimized for missing scenarios. It is shown that controlled over-fitting by suggested algorithms will improve prediction accuracy in various cases. Simulation results approve our heuristics in enhancing the prediction accuracy.